Figure-2.54 shows a block of mass m is placed on an inclined wedge of mass M If the system is released from rest find the acceleration of m and M.
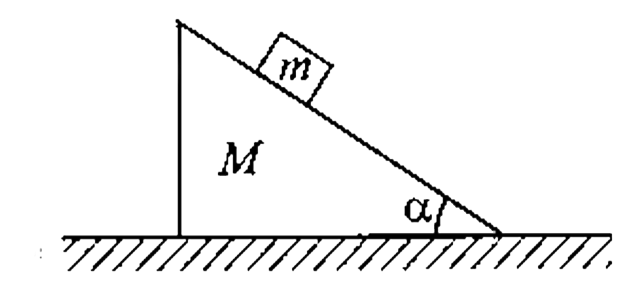
Step by step video & image solution for Figure-2.54 shows a block of mass m is placed on an inclined wedge of mass M If the system is released from rest find the acceleration of m and M. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Practice Exerice 2.1
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Practice Exerice
4 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
Figure-2.64 shows a block of mass M supporting a bar of mass m through a pulley system. If system is released from rest, find the acceleration of block M and the tension in the strings
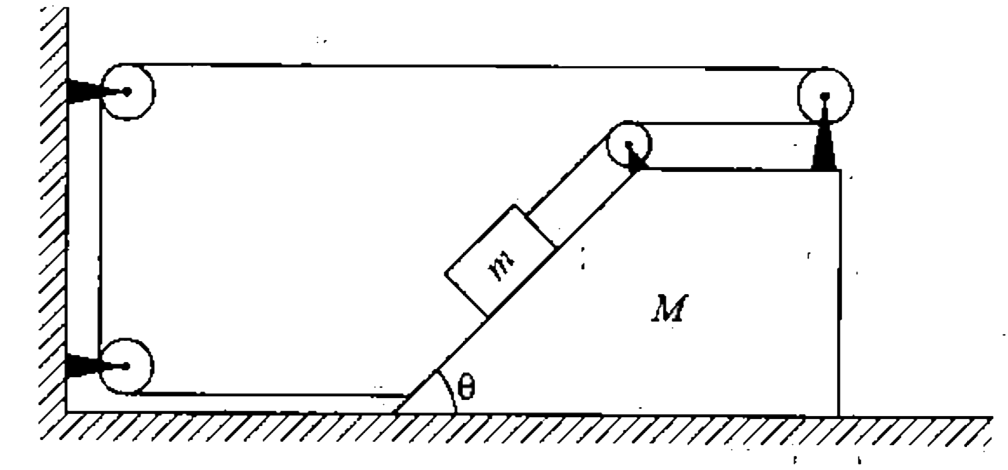
View SolutionIn the system shown in the figure all surfaces are smooth, pulley and string are massless. The string between the two pulleys and between pulley and block of mass 5 m is parallel to the incline surface of the block of mass 4 m. The system is released from rest. Find the acceleration of the block of mass 4 m . [tan37∘=34]
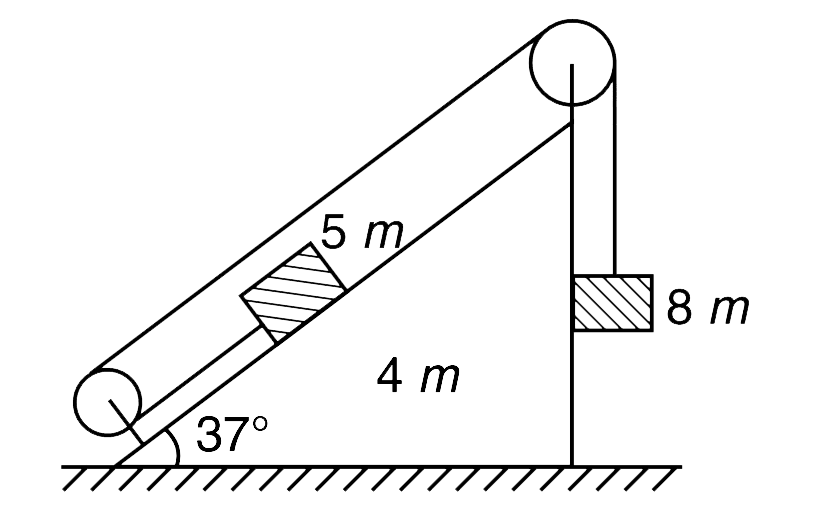
View Solution
Knowledge Check
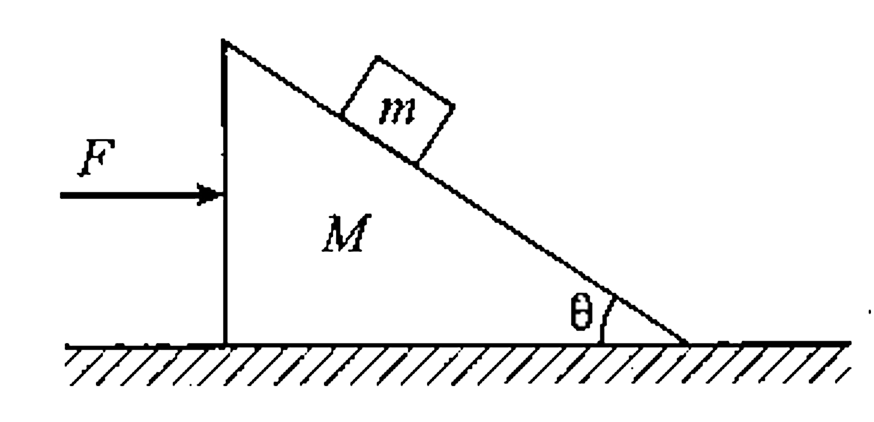
In fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
 Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ
Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θFigure shown a block of mass m placed on a smooth wedge of mass M. Calculate the minimum value of M' and tension in the string, so that the block of mass m will move vertically downwards with acceleration 10ms−2
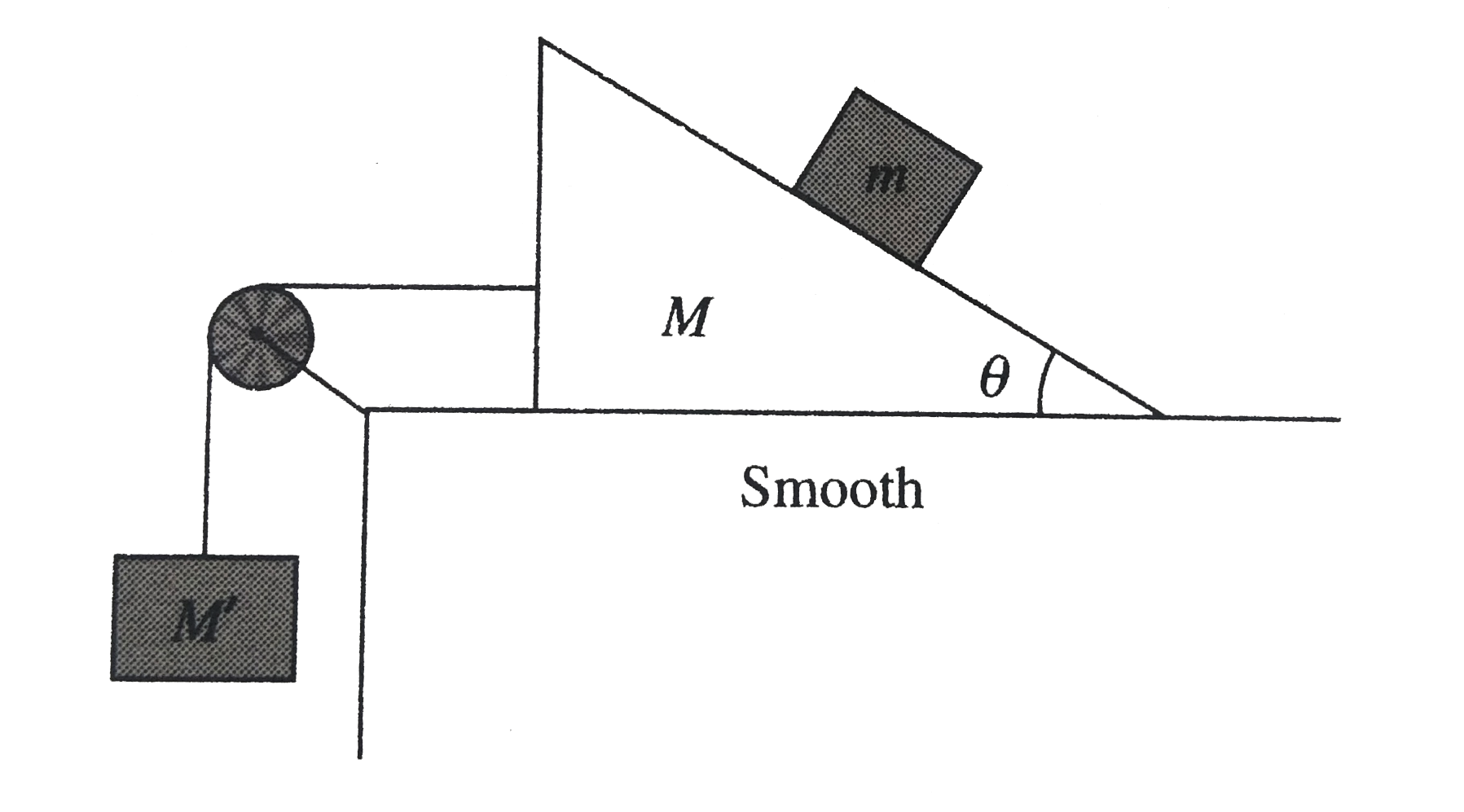 AThe value of M' is Mcotθ1−cotθBThe value of M' is Mtanθ1−tanθCThe value of tension in the string is MgtanθDThe value of tension is Mgcotθ
AThe value of M' is Mcotθ1−cotθBThe value of M' is Mtanθ1−tanθCThe value of tension in the string is MgtanθDThe value of tension is Mgcotθ
In the Fig. shown, mass 'm' is being pulled on the incline of a wedge of mass M. All the surface are smooth. Find the acceleration of the wedge.
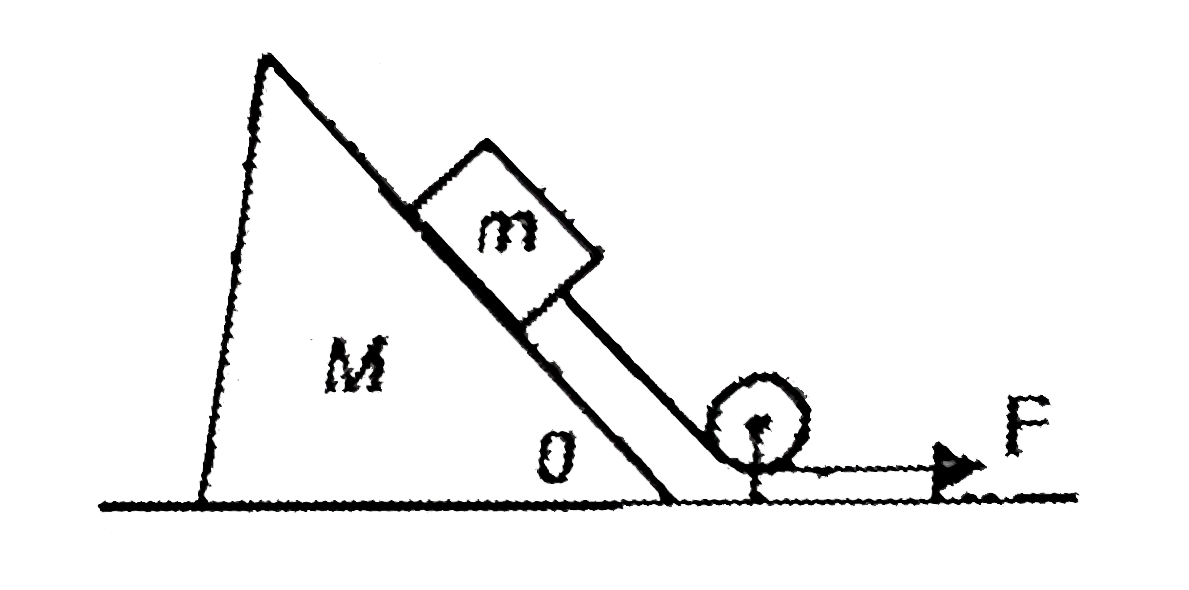
View SolutionFigure-2.52 shows a box of mass m is placed on a wedge of mass M on a smooth surface. How much force F is required to be applied on M so that during motion m remains at rest on its surface
View SolutionTwo blocks m1 and m2 are placed on a smooth inclined plane as shown in figure. If they are released from rest. Find :
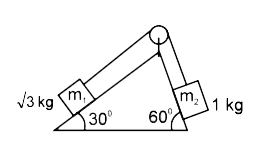
(i) acceleration of mass m1 and m2
(ii) tension in the string
(iii) net force on pulley exerted by string.
View SolutionFigure shows a fixed wedge on which two blocks of masses 2kg and 3kg are placed on its smooth inclined surfaces. When the two blocks are released from rest, find the acceleration of centre of mass of the two blocks.

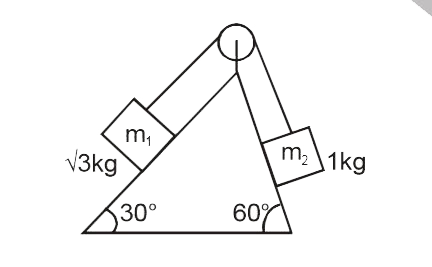
View SolutionTwo block m1 and m2 are placed on a smooth inclined plane as shown in figure. It they are released from rest.
Find :
(i) acceleration of mass m1 and m2
(ii) tension in the string
(iii) net force on pulley exerted by string
View SolutionA triangular wedge W having mass M is placed on an incline plane with its face AB horizontal. Inclination of the incline is θ. On the flat horizontal surface of the wedge there lies an infinite tower of rectangular blocks. Blocks 1, 2, 3, 4 ………. have masses M,M2,M4,M8 ......... respectively . All surfaces are smooth. Find the contact force between the block 1 and 2 after the system is released from rest. Also find the acceleration of the wedge.
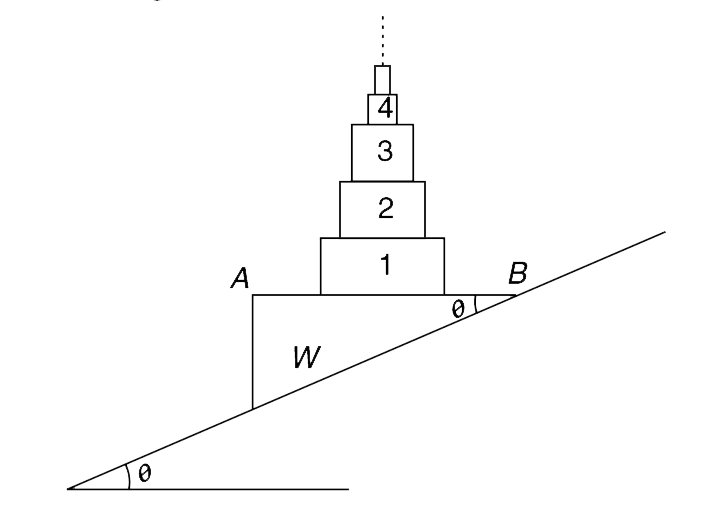
View Solution
