Figure 26-21 shows wire section 1 of diameter D1=4.00R and wire section 2 of diameter D2=1.75R, connected by a tapered section. The wire is Copper and carries a current. Assume that the current is uniformly distributed across any cross-sectional area through the wire's width. The electric potential change V along the length L= 2.00 m shown in section 2 is 10.0μV. The number of charge carners per unit volume is 8.49×1028m−3. What is the drift speed of the conduction electrons in section 1? 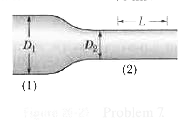
The correct Answer is:6.22×10−9m/s
Topper's Solved these Questions
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Single Corret Choice Type)
39 Videos
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Linked Comprehension)
5 Videos
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Checkpoints
6 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - CHECK POINTS
6 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
Similar Questions
A uniform current I is flowing in a long wire of radius R. If the current is uniformly distributed across the cross-sectional area of the wire, then
View SolutionA long straight wire of radius a carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetis field at (a)/(2)and(2a) is
View Solution
Knowledge Check
A uniform current I is flowing in a long wire of radius R. If the current is uniformly distributed across the cross-sectional area of the wire, then
Amagnetic field increases linearly from centre to surfaceBmagnetic field decays inversely with distance r from the centre of wire for r>RCmagnetic field at the centre of wire is zeroDNone of the aboveA long cylindrical wire carries a steady current which is uniformly distributed across its cross section. Which of the following is true?
AMagnetic field is zero at the centre.BElectric field is zero at the centre.CElectric field just outside the cylinder is zero.DMagnetic field just outside the cylinder is zero.A long straight wire of radius a carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetis field at (a)/(2)and(2a) is
A(1/2)B(1/4)C4D1
Figure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionA length of copper wire carries a current of 3.5 A uniformly distributed through its cross section. Calculate the energy density of (a) the magnetic field and (b) the electric field at the surface of the wire. The wire diameter is 2.5 mm, and its resistance per unit length is 3.3 Ω/km.
View SolutionA long staright wire of radius a carries a steady current I. The curent is unifromly distributed over its cross-section. The ratio of the magnetic fields B and B' , at radial distances a2 and 2a respectively from the axis of the wire is:
View Solution
