Figure. Illustrates logarithmic electric conductance as a function on reciprocal temperature ( T in KK units) for some
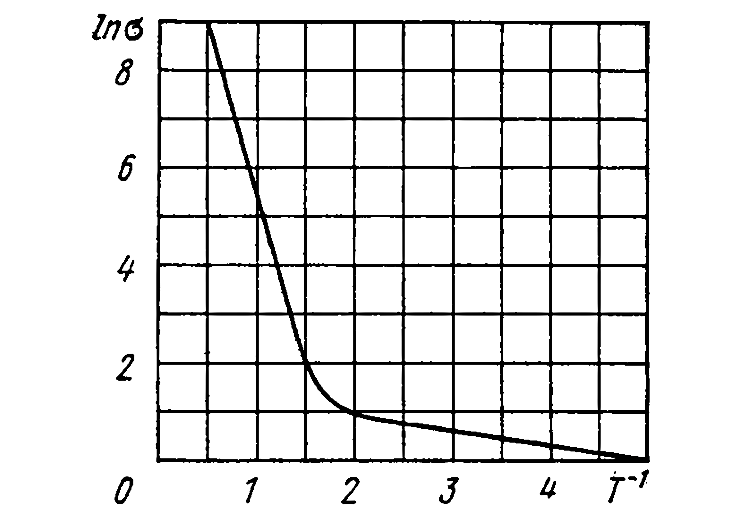
n type semiconductor. Using this plot, find the width of the forbiden band of the semiconductor and the activation energy of donor levels.
At high temperatures (small values of T−1) most of the conductivity is infrinsic i.e, it is due to the transition of electrons from the upper levels of the valance band into the lower levels of conduction vands.
For this we can apply approximately the formula
σ=σ0exp(−Eg2kT)
or In σ=Inσ0−Eg2kt
From this we get the band gap
Eg=−2kΔInσΔ(1/T)
The slope must be calculated at small 1T. Evaluation gives −ΔInσΔ(1T)=7000K
Hence Eg=1.21eV
At low temperature (high values of 1T) the conductance is mostly due to impurities. If E0 is the ionization energy of donor levels then we can write the approximate formula (valid at low temperature)
σ'=σ'0exp(−E02kT)
So E0=02kTΔInσ'Δ(1T)
The slope must be calculated at low temperatures. Evaluation gives the slope
−ΔInσ'Δ(1T)=13×1000K
Then E0~0.057eV
Topper's Solved these Questions
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Radioactivity
35 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Nuclear Reaction
42 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Properties Of Atom
69 Videos
- DIRECT CURRENTBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions
15 Videos
Similar Questions
Knowledge Check
In an n-type semiconductor, the donor energy level lies
Aat the centre of the energy gap.Bjust below the conduction band.Cjust above the valance band.Din the conduction band.An n-type semiconductor has donor levels at 500 meV above the valence band, the frequnecy of light required to create a hole is nearly
A8×1013HzB12×1013HzC22×1013HzD15×1013Hz
The donor energy level is close to the _____________band in n type semiconductor
View SolutionDraw the energy band diagram of a n-type semiconductor. Deduce an expression for conductivity of a n-type semiconductor.
View SolutionAn n-type semiconductor has donor levels at 500 meV above the valence band, the frequnecy of light required to create a hole is nearly
View SolutionIn a semiconductor energy gap between the impurites level and conduction band is 1 me V is it an n type or p type of semiconductor
View SolutionDistinguish between n-type and p-type semiconductors on the basis of energy-band diagrams. Explain the process of conduction in both type of materials.
View SolutionAn ideal crystal has the same unit cell containing the same lattice points throughout the whole of crystal. But such ideal crystals exist only at 0 K temperature. However, during the formation of crystal structure, certain defects are produced. These defects are point defects, line defects, vacancy defects, interstitial defects or impurity defects. Due to these defect, the crystals exhibit different properties. Presence of delocalised electrons make the metals conductor of electricity . Germanium and silicon are the most important commericial semiconductors. By adding impurities such as arsenic and boron, n and p - type semiconductors can be synthesised. Various combinations of n and p type semiconductors are used to make electronic components.
Name the type of point defect that occurs in a crystal of zinc sulphide. Will it increase, decrease or not change the density ?
View Solution
