Figure is the plot of the stopping potential versus the frequency of the light used in an experiment on photoelectric effect. Find (a) the ratio h/e and (b) the work function.
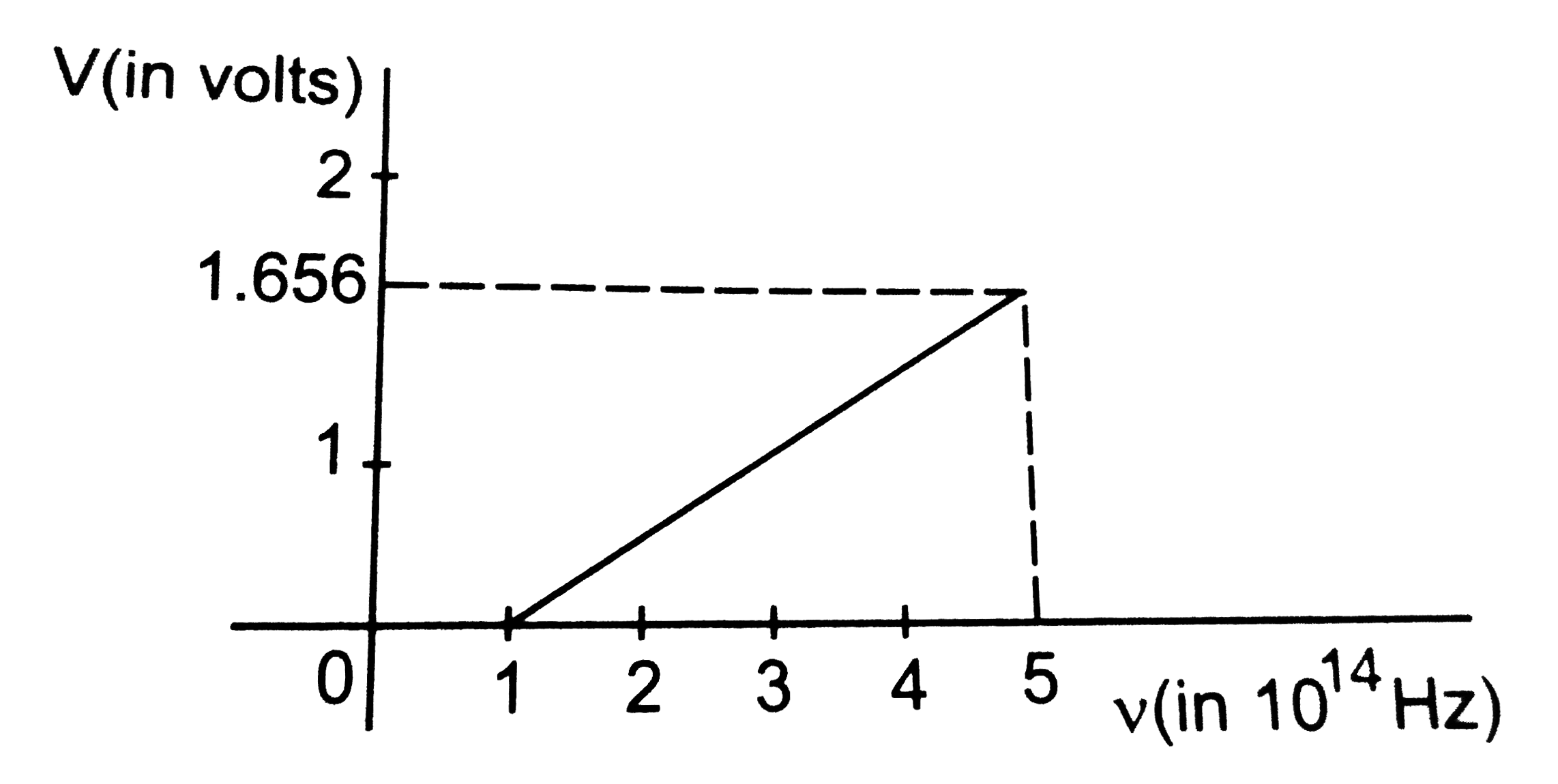
We have to take two cases
Case - I v0=1.656 v=5×1014Hz
Case -II v0=0
v=1×1014Hz
(b) We know ev0=hv−W0
1.656e=h×5×1014−W0
0=5h×1014−5W0
1.6556e=4W0
⇒W0=1.6564eV
=0.414eV
(a) Putting the value of W_0 in equation (2)
⇒5W0=5h×1014
⇒5×0.414=5×h×1014
⇒h=4.414×10−15eV−s
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - question for short answer
13 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - objective II
7 Videos
- PERMANENT MAGNETSBOOK - HC VERMA ENGLISHCHAPTER - PERMANENT MAGNETSEXERCISE - Short Answer
11 Videos
- PHOTOMETRYBOOK - HC VERMA ENGLISHCHAPTER - PHOTOMETRYEXERCISE - All Questions
38 Videos
Similar Questions
A non-monochromatic light is used in an experiment on photoelectric effect. The stopping potential
View SolutionThe electric field associated with a light wave is given by E=E0sin[(1.57×107m−1(x−ct)]. Find the stopping potential when this light is used in an experiment on photoelectric effect with a metal having work - function 1.9 eV.
View Solution
Knowledge Check
The stopping potential as a function of the frequency of the incident radiation is plotted for two different photoelectric surfaces A and B . The graphs show that work function of A is
 AlessBmoreCequalDnothing can be said
AlessBmoreCequalDnothing can be said
The electric field associated with a light wave is given by E=E0sin[(1.57x107m−1(x−ct)]. Find the stopping potential when this light is used in an experiment on photoelectric affect with a metal having work - function 1.9 eV.
View SolutionWhen stopping potential is applied in an experiment on photoelectric effect, no photo current is observed. This means that
View SolutionThe electric field associated with a light wave is given by E=E0sin[(1.57×107m−1)(ct−x)]. Find the stopping potential when this light is used in an experiment on a photoelectric effect with the emitter having work function 2.1eV. h=6.62×10−34Js.
View SolutionGraph between stopping potential and frequency of light as shown find the work function

View SolutionFigure shows the graph of stopping potential verus that frequency of a photosensitive metal. The plank's constant and work funcation of the metal are
_S01_035_Q01.png)
View SolutionThe following figure shows a graph for the stopping potential as a function of the frequency of incident light illuminating a metal surface. Find the photoelectric work function for this surface.
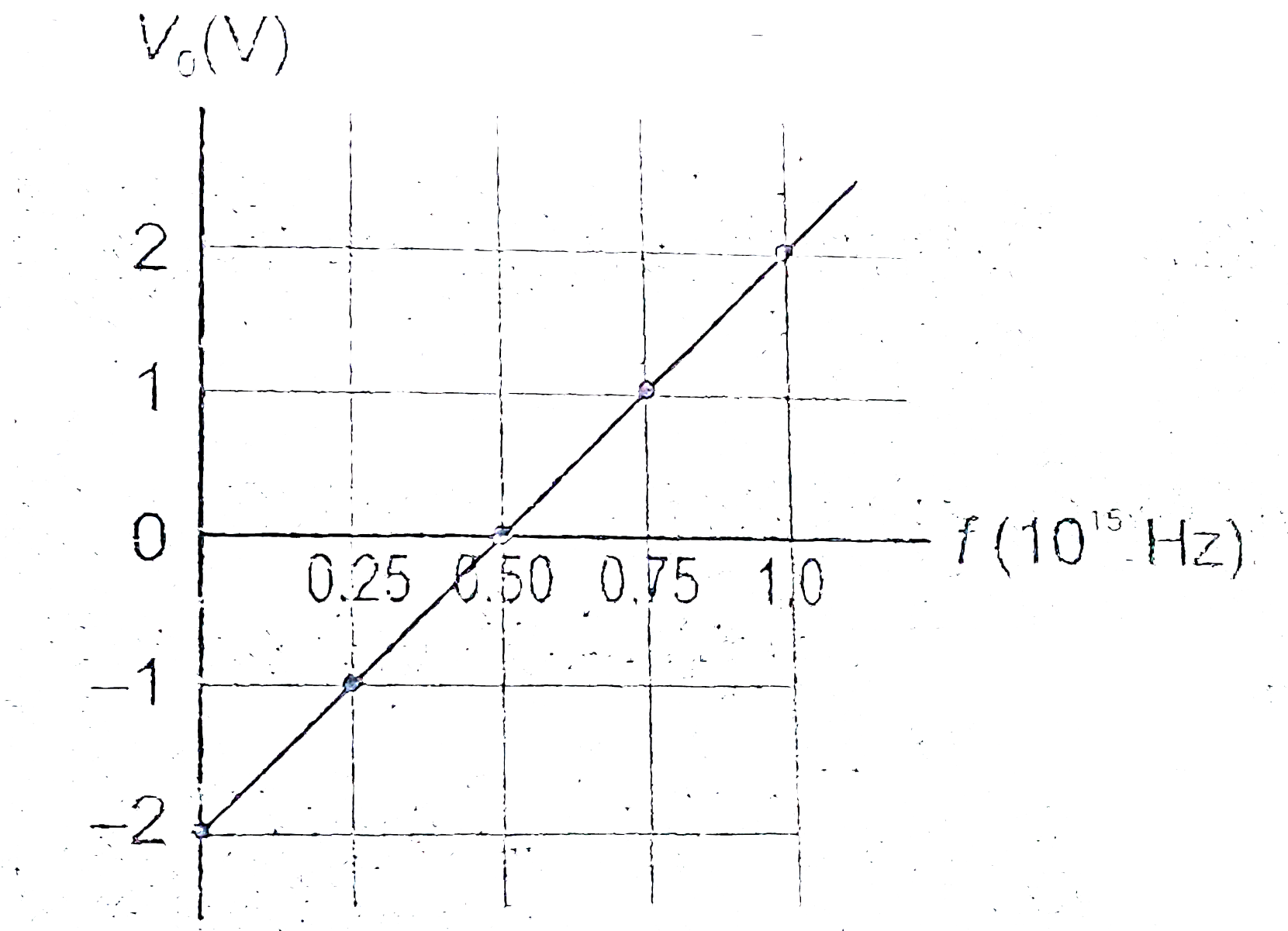
View SolutionIf the frequency of light in a photoelectric experiment is doubled the stopping potential will
View Solution
