figure shown a partical mass m=100g attaches with four identical spring , each of length l=10cm . Initical tension in each spring is F0=25N. Neglecting gravity , Calculate the period of small obscillation of the article along a line perpenducular to the plane of the figure .

Let tha prtical be displaced singhtly through x along a line normal to the plane of figure . Then each spring is further elongated . Since , springs are indentical , therefore increase in tension of each spring will be the same. Let this increase be df0

First consider force exerted by spring APandCP only as shown in figure
Restoring force produced by these two spring =(F0+dF0)22sinθ.
Since x is very small, hterefore , sinθ=xll.
Neglecting produced of veru small quantities, restoring force produced by these two springs =2F0xll
Similarly, resorting force produced by two remaining springs BPandDP will also be equal to (2F0xll)
Resultant resoring force.
F=2×(2F0xl)=4F0lx
Restoring acceleration is directly proportinal to displacement x, therefore ,the partical executes SHM
Its period T=2π√displacementacceleration
=2π√ml4F0=π√ml4F0=0.02πs
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A solid cylinder of mass M=10kg and cross - sectional area A=20cm2 is suspended by a spring of force contant k=100N/m and hangs partically immersed in water. Calculate the period of small oscillation of the cylinder.
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View Solution
Knowledge Check
The following figure shows a particle of mass, m, attached with four identical springs, each of length l. Initial tension in each spring is F0. The period of small oscillations of the particle along a line perpendicular to the plane of the figure is (neglect gravity)
 Aπ√mlF0B2π√mlF0C2π√ml2F0Dπ√ml4F0
Aπ√mlF0B2π√mlF0C2π√ml2F0Dπ√ml4F0A particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
 AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mK
AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mKA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk
Spring mass system is shown in figure. Find the elastic potential energy stored in each spring when block is at its mean position. Also find the time period of vertical oscillations. The system is in vertical plane.

View SolutionSpring mass system is shown in figure. Find the elastic potential energy stored in each spring when block is at its mean position. Also find the time period of vertical oscillations. The system is in vertical plane.

View SolutionTwo identical particles each of mass 0.5kg are interconnected by a light springs of stiffness 100N/m, time period of small oscillation is ….
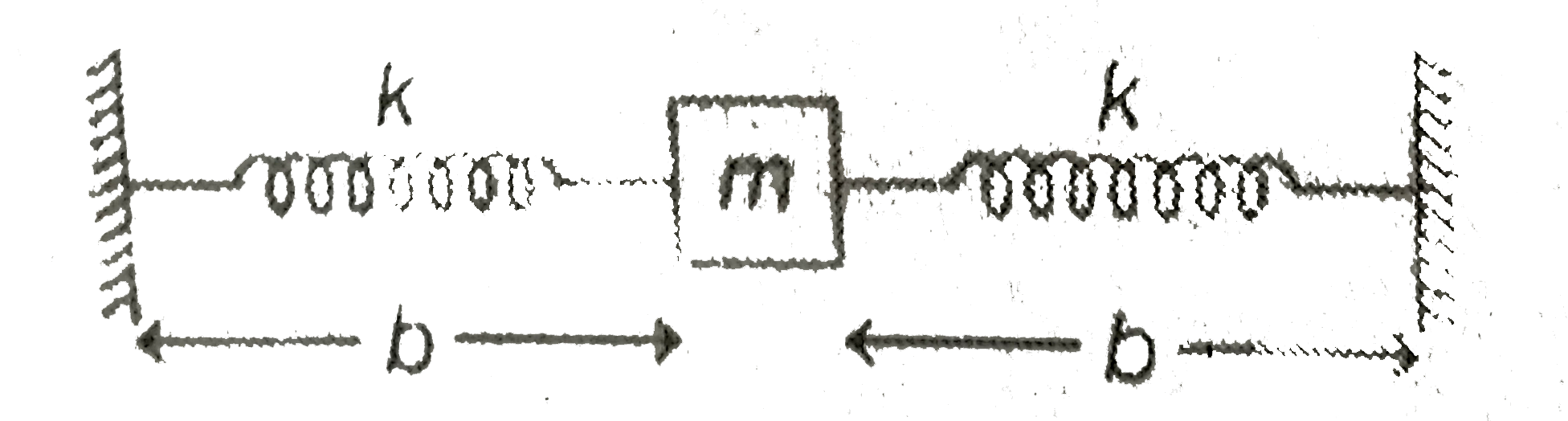
View SolutionIn the figure, a block of mass m is rigidly attached to two identical springs of stiffness k each. The other ends of the springs are connected to the fixed wall. When the block is in equilibrium, length of each spring is b, which is greater than the natural length of the spring. The time period of the oscillation of the block if it is displaced by small distance perpendicular to the length of the springs and released. Space is gravity free.
View SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:

View Solution
