A uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:

2π√mk
2π√2m3k
π√3m2k
π√2m3k
Let centre of disc is displaced by x from its equilibrium position (spring was in its natural length). Now calculate the torque about lowest point of disc.
k.32R.3x2=32mR2aR
3kx2m=a
So, T=2π√2m3k
Topper's Solved these Questions
Similar Questions
A small block is connected to a mass less rod, which is turn is attached to a spring of force constant k as shown in Fig. The blcok is displaced down slightly, and left free. Find time period of small oscillations.
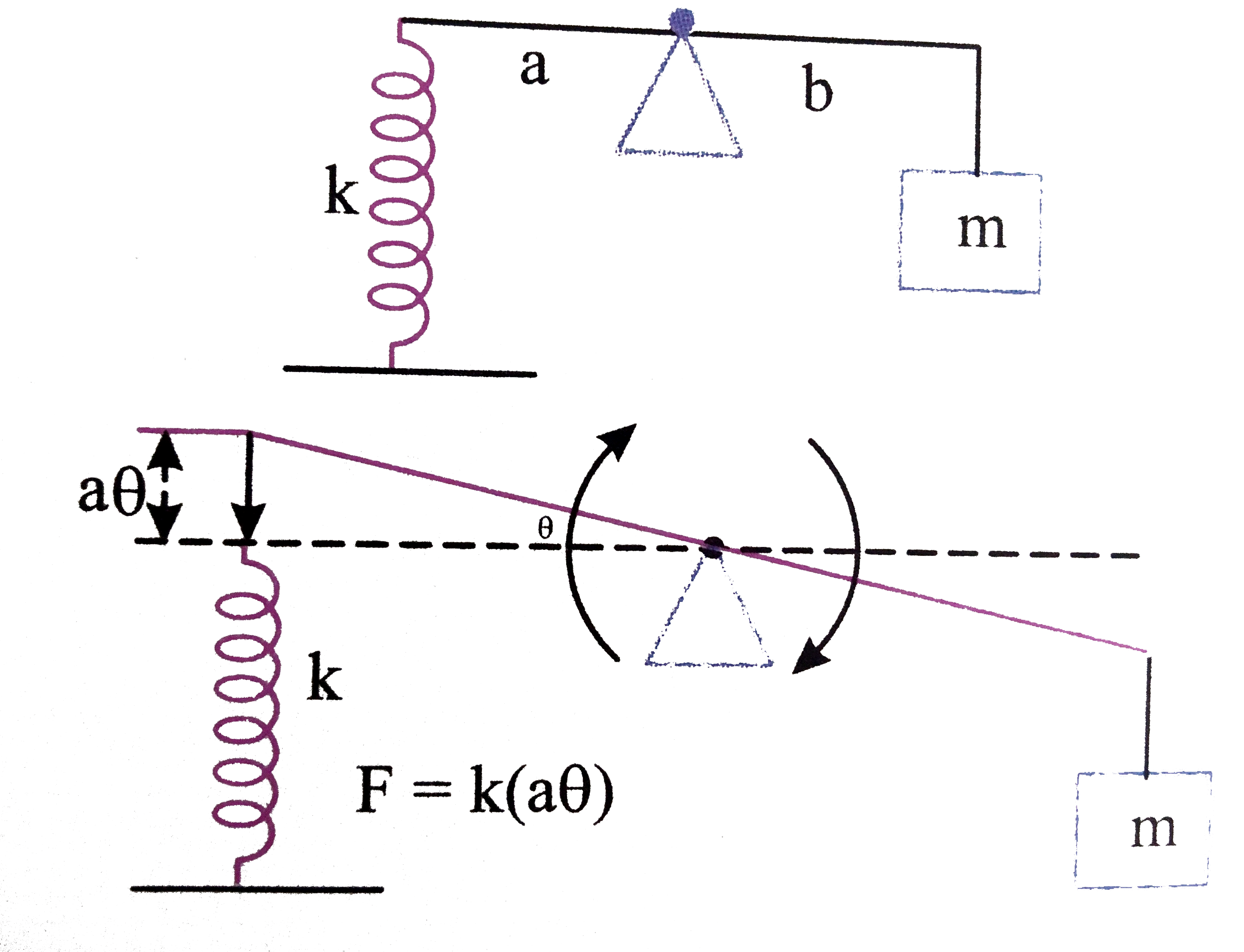
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
Knowledge Check
A particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkA mass m is suspended from a spring of force constant k and just touches another idential spring fixed to the floras shown in the figure. The time period of small oscillation is
 A2π√mkBπ√mk+π√mk/2Cπ√m3k/2Dπ√mk+π√m2k
A2π√mkBπ√mk+π√mk/2Cπ√m3k/2Dπ√mk+π√m2k

A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
View SolutionA solid cylinder is attached to a horizonatal massless spring as shwn in figure.If the cyclinder rolls without slipping, the time period of oscillation of the cyclinder is

View SolutionA block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.

View SolutionA load of mass M is attached to the bottom of a spring of mass 'M/3' and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
View SolutionThree springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
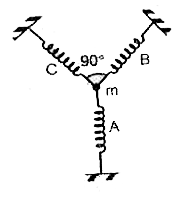
View Solution