Figure shows a circuit having a coil of resistance R=2.5Ω and inductance L connected to a conducting rod of radius 10cm with its center at P.

Assume that friction and gravity are absent and a constant uniform magnatic field of 5T exists as shown in figure. At t=0, the circuit is switched on and simultaneously a time-varying external torque is applied on the rod so that it rotates about P with a constant angular velocity 40rads−1. Find the magnitude of this torque (in mNm) when current reaches half of its maximum value. Neglect the self inductance of the loop formed by the circuit.
The correct Answer is:(5)
Induced EMF=12Bωl2
Maximum current: i0=Bωl22R
Torque about the hinge P is
τ=l∫0i(dx)Bx⇒τ=12iBl2
Putting i=i0/2, we get: τ=B2Ωl48R=5mNm
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Archives (fills In The Blanks)3videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Archives (single Correct )8videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (linked Compreshension)36videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
Similar Questions
The diagram shows a circuit having a coil of resistance R=2.5(Ω) and inductance L connected to a conducting rod PQ which can slide on perfectly conducting circular ring of radius 10 cm with its centre at 'P'. Assume that friction and gravity are absent and a constant uniform magnetic field of 5 T exist as shown in Fig.
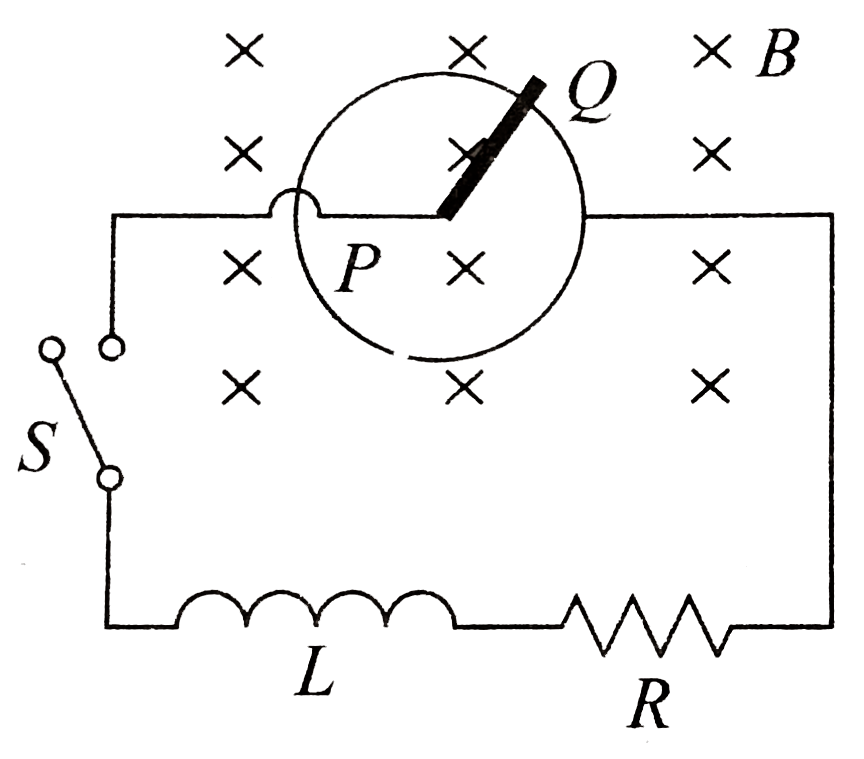
At t = 0, the circuit is switched on and simultaneously a time varying external torque is applied on the rod so that it rotates about P with a constant angular velocity 40rad/s. Find magnitude of this torque (in milli Nm) when current reaches half of its maximum value. Neglect the self-inductance of the loop formed by the circuit.View SolutionThe circuit shows a resistance, R=0.01Ω and inductance L=3mH connected to a conducting rod PQ of length l=1m which can slide on a perfectly conducting circular arc of radius l with its center at P. Assume that friction and gravity are absent and a constant uniform magnetic field b=0.1T exists as shown in the figure. At t=0, the circuit is seitched on a simultaneously an external torque is applied on the rod so that it rotates about P with a constant angular velocity ω=2rad/sec. Find the magnitude of this torque (inN-m) at t=(0.3In 2) second.
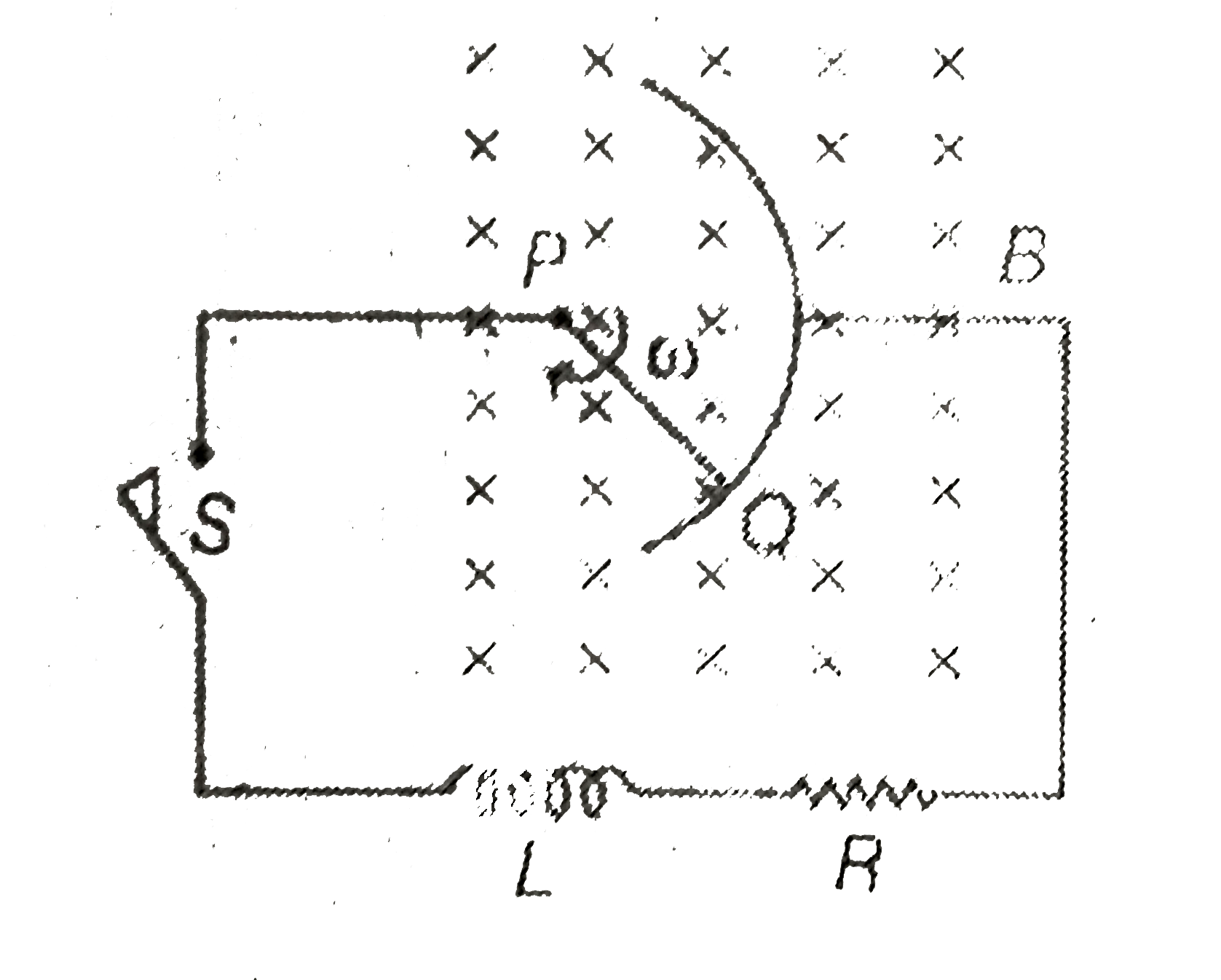 View Solution
View SolutionA resitance R=1kΩ connected to a conducting rod PQ that can slide on a conducting circular ring of radius 2m with center at P. A constant uniform magnetic field 10 Tesla exist as shown in figure. At t=0, switch 'S' is closed and simulaneously an external torque is applied on the rod so that it rotates with constant angular velocity 20rad/sec. The magnitude of power delivered by external is 20K Watt. Find the value of K. (Neglect the gravity, friction and self inductance of circular loop)
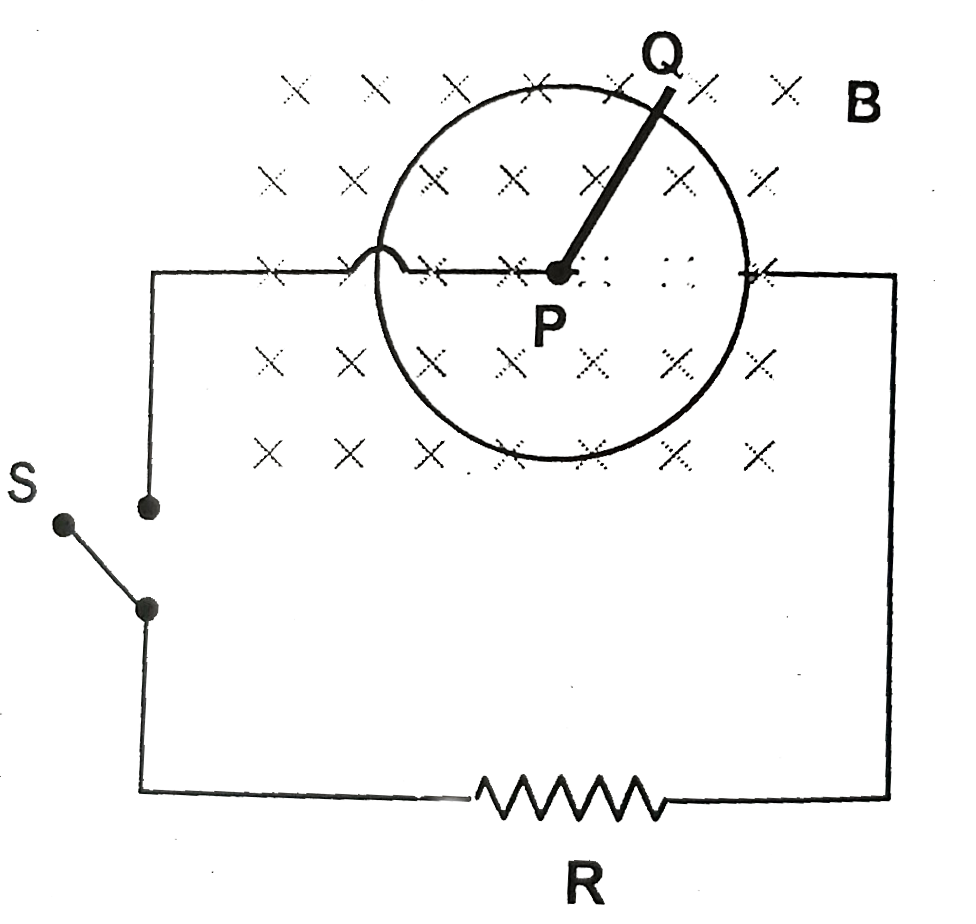 View Solution
View SolutionThe power factor of an AC circuit having resistance (R) and inductance (L) connected in series and an angular velocity ω is
View SolutionA circular conducting coil of radius r0, having resistance R is placed in a time varying transverse uniform magnetic field B=4t2 as shown in the figure. The current in the coil at time t = 2 s is (consider all quantities are in Si units)
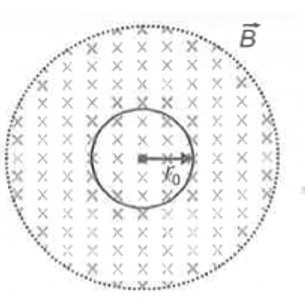 View Solution
View SolutionThe figure shows a circuit.
When the circuit is switched on, the ammeter reads 0.5A.
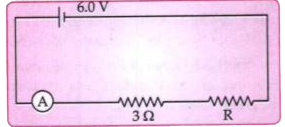
Calculate the value of the unknown resistor R.View SolutionEight resistances each of resistance 5Ω are connected in the circuit as shown in figure. The equivalent resistance between A and B is
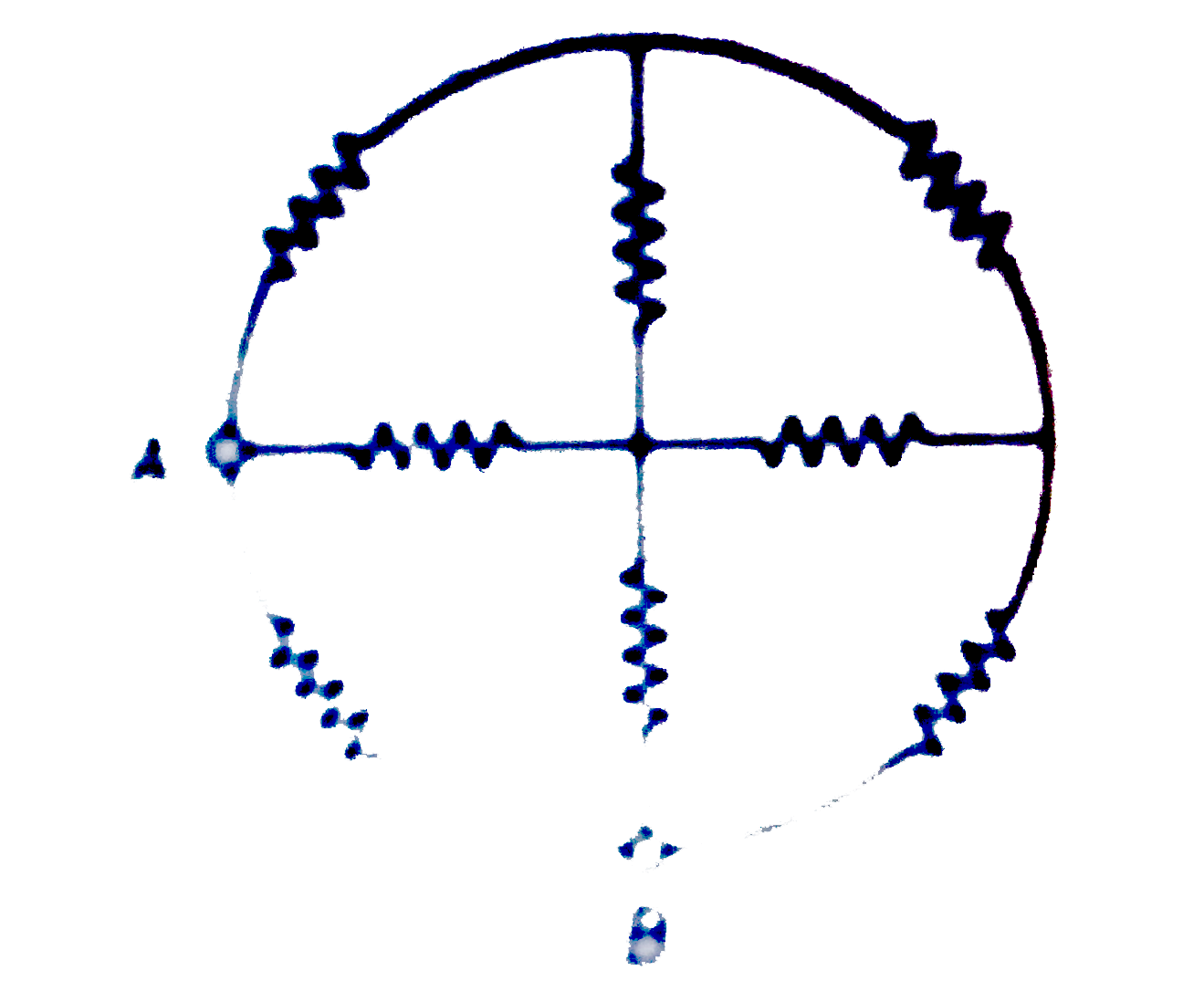 View Solution
View SolutionThe figure shows a circuit.
When the circuit is switched on, the ammeter reads 0.5A.
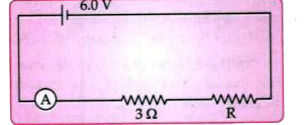
Calculate the power dissipated in the 3Ω resistor.View SolutionIn the circuit shown in figure, circuit is closed at time t=0. At time t=ln(2) second
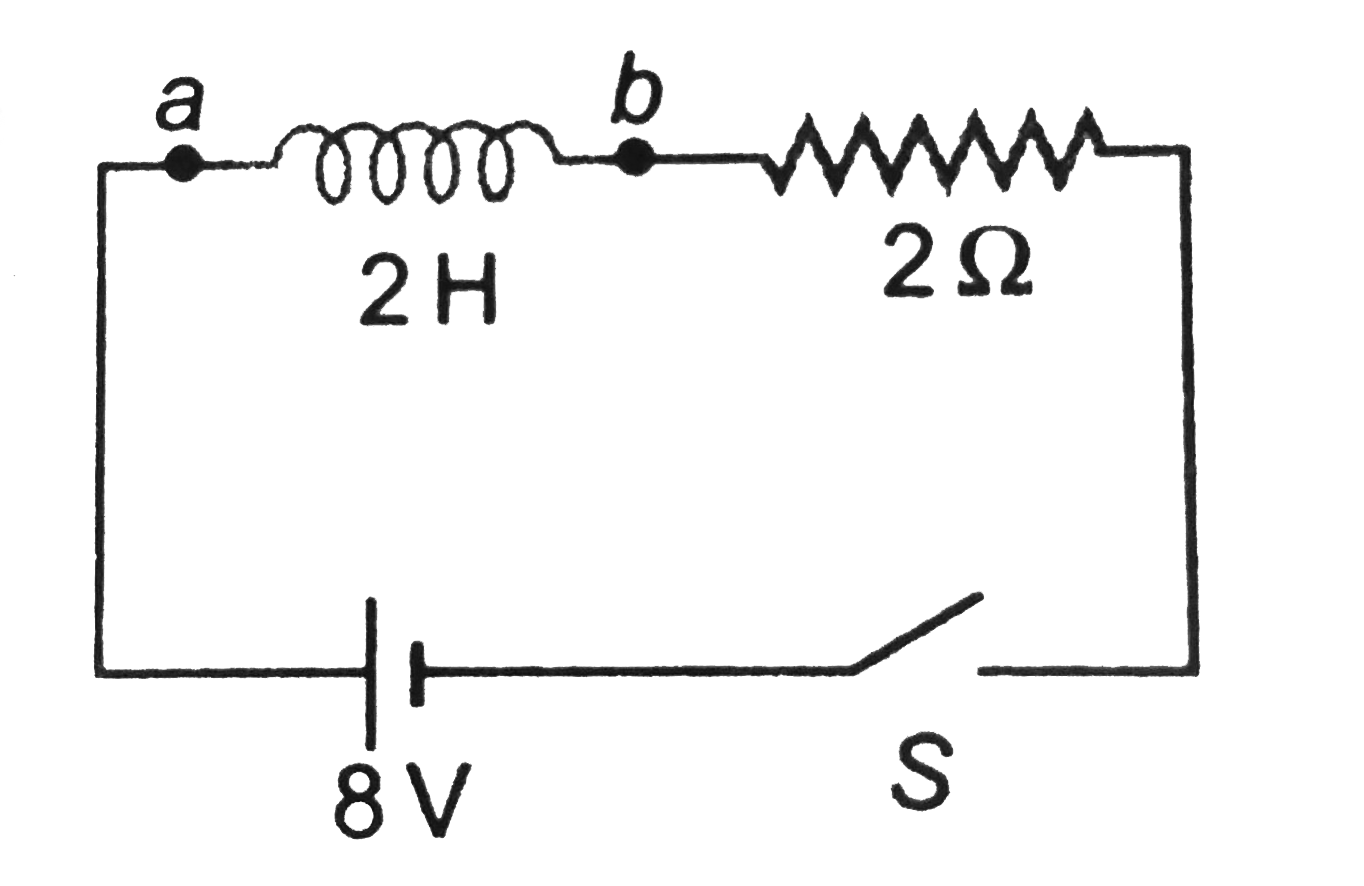 View Solution
View SolutionA coil of inductance 5.0 mH and negligible resistance is connected to an alternating voltage V=10sin(100t). The peak current in the circuit will be:
View Solution

