Figure shows a conducting rod of length l=10cm, resistance R and mass m=100mg moving vertically downward due to gravity. Other parts are kept fixed. Magnetic filed is B=1T. MNandPQ are vertical, smooth, the capacitor is C=10mF. The rod is released from rest. Find the maximum current (in mA) in the circuit.
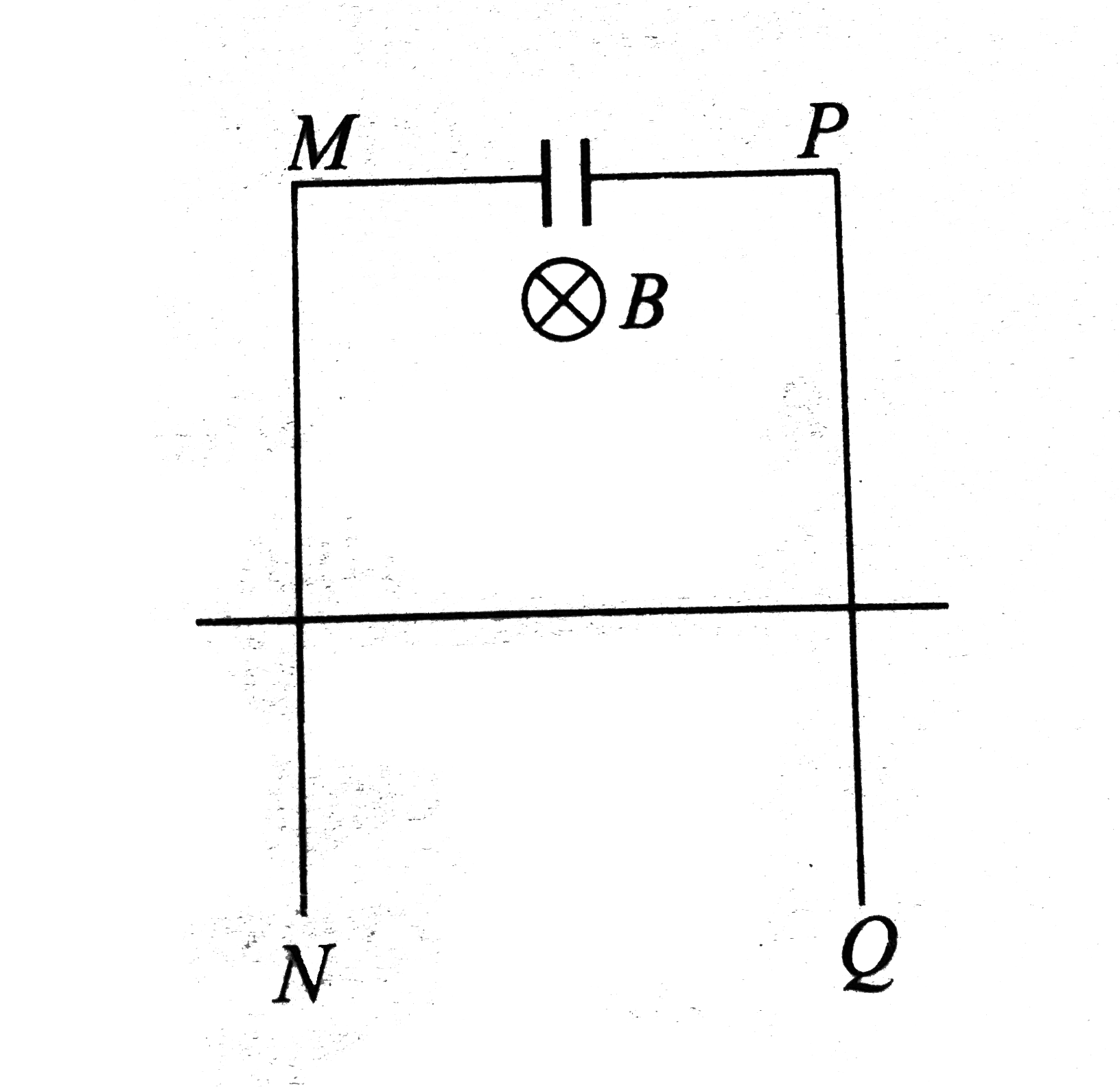
The correct Answer is:5
, 
By Newton's law, mg=ilB=mdvdt (i)
Using KVLblv=iR+qC
Differenting (ii) w.r.t. time, we get
Bldvdt=Rdidt+ic
Eliminating dvdt from equations (i) and (iii), we get
mg−ilB=mBl[Rdidt+iC]
→ mgBl−iB2l2=m(Rdidt+miC)
I will be maximum when dict=0. Use this in equation (iv)
→ mgBlC=i(B2l2C+m)
→ imax=mgBlCm+B2l2C
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Archives Fill In The Blanks3videos
ELECTROMAGNETIC INDUCTION
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Archives Single Correct11videos
ELECTROMAGNETIC INDUCTION
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Linked Comprehension36videos
ELECTROMAGNETIC INDUCTION
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK40videos
ELECTROMAGENTIC INDUCTION
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
Similar Questions
In the figure shown a conducting rod of length l, resistance R and mass m is moved with a constant velocity v. The magnitude field B varies with time t as B=5t, what t is time in second. At t=0 the area of the loop containing capacitor and the rod is zero and the capacitor is uncharged. the rod started moving at t=0 on the fixed smooth conducting rails which have negligible resistance. Find the current in the circuit as a function of time t.
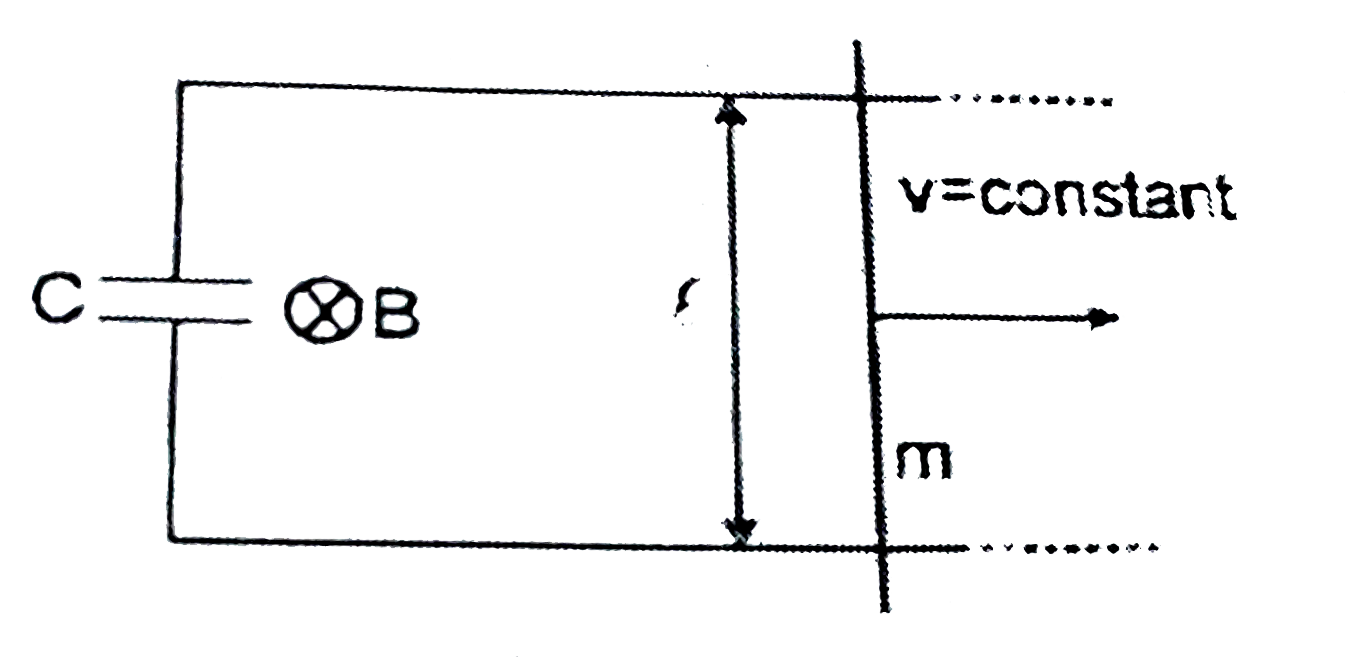
View SolutionA thin conducting rod MN of mass 20gm, length 25cm and resistance 10Ω is held on frictionless long perfectly conducting vertical rails as shown in the figure. There is a uniform magnetic field B0=4T directed perpendicular to the plane of the rod-rail arrangement. The rod is released from rest at time ? = 0 and it moves down along the rails. Assume air drag is negligible. Match each quantity in List-I with an appropriate value from List-II, and choose the correct option.
[Given: The acceleration due to gravity g=10ms−2 and e−1=0.4]
View Solution
Knowledge Check
- Question 1 - Select One
A weightless rod of length 2l carries two equal masses 'm', one tied at lower end A and the other at the middle of the rod at B. The rod can rotate in vertical plane about a fixed horizontal axis passing thriugh C . The rod of is released from rest in horizontal possion. The speed of the mass B at the instant rod become vertical is:
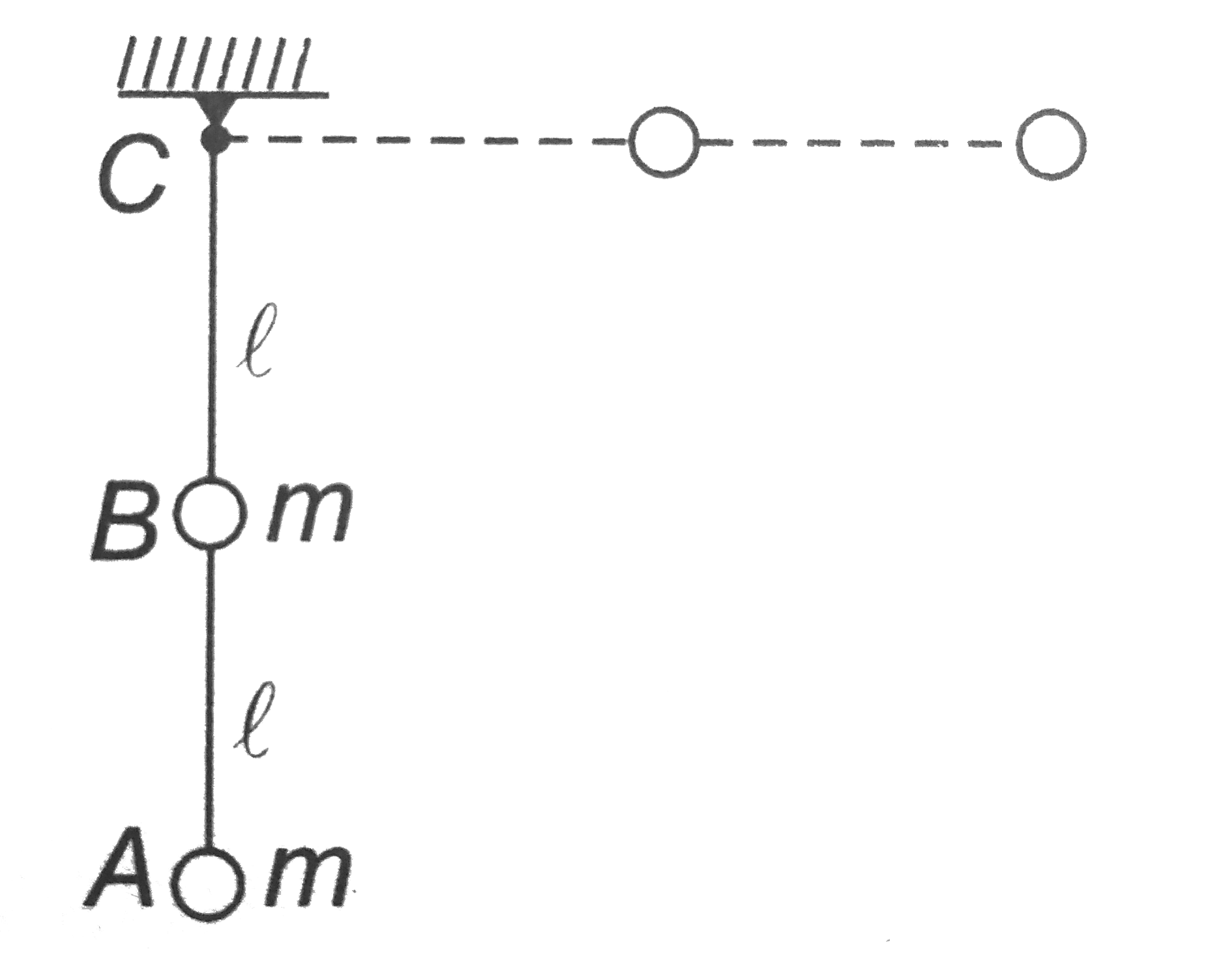A√3gl5B√4gl5C√6gl5D√7gl5 - Question 2 - Select One
Figure shows a conducting rod of negligible resistance that can slide on smooth U− shaped rail made of wire of resistance 1Ω/m. Position of the conducting rod at t=0 is shown. A time t dependent magnetic filed B=2tTesla is switeched on t=0
At t=0, when the magnetic field to switched on, the conducting rod is moved to the left at constant speed 5cm/s by some external means. The rod moves perpendicular to the rails. At t=2s, induced emf has magnitude.A0.12VB0.08VC0.04VD0.02V - Question 3 - Select One
Figure shows a conducting rod of negligible resistance that can slide on smooth U-shaped rail made of wire of resistance 1Ω/m. Position of the conducting rod at t=0 is shown. A time dependent magnetic field B=2t tesla is switched on at t=0
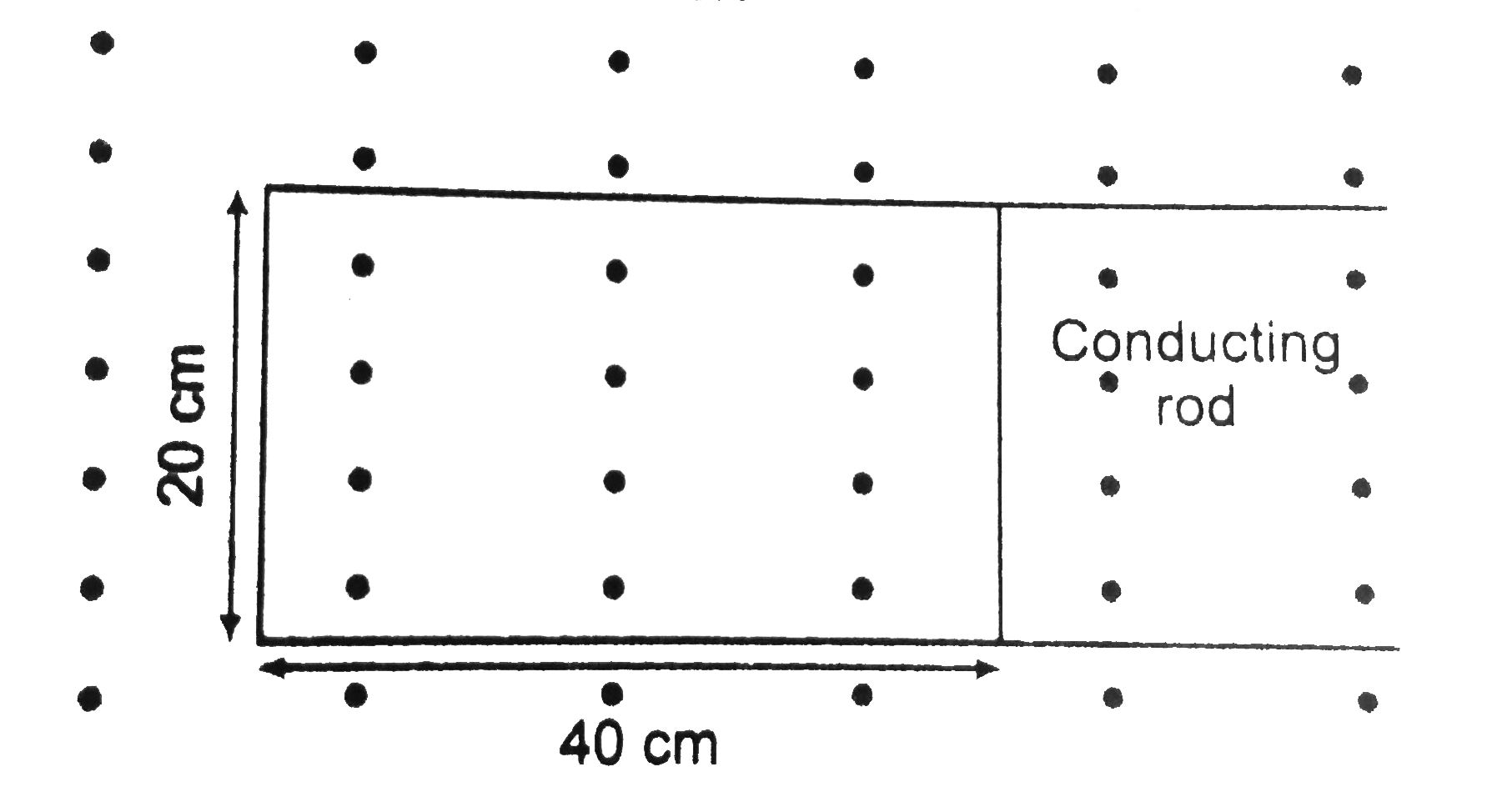
At t=0, when the magnetic field is switched on, the conducting rod is moved to the left at constant speed 5cm/s by some external means. At t=2s, net induced emf has magnitudeA0.12VB0.12VC0.04VD0.02V
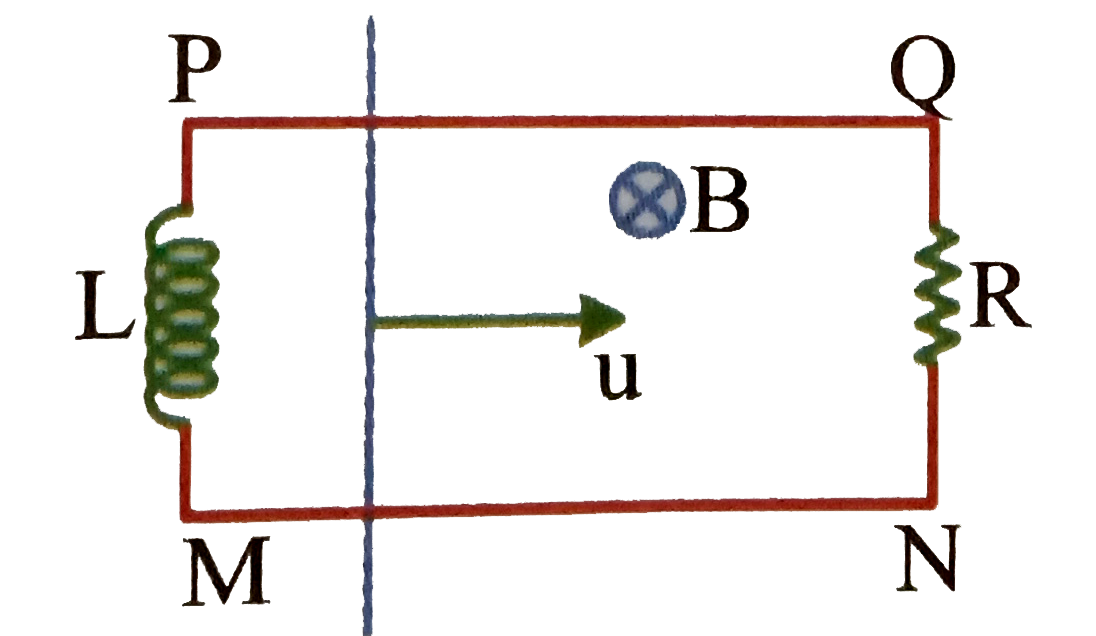
In the figure, a conducting rod of length l=1 meter and mass m=1kg moves with initial velocity u=5m/s. On a fixed horizontal frame containing inductor L=2H and resistance R=1W. PQ and MN are smooth, conducting wires. There is a uniform magnetic field of strength B=1T. Initial there is no current in the inductor. Find the total charge in coulomb, flown through the inductor by the time velocity of rod becomes vf=1m/s and the rod has travelled a distance x=3 meter.
View SolutionIn the figure shown a conducting rod of length l, resistnace R and mass m is moved with a constant velocity v.The magnetic field B varies with time t as B=5t, where t is time in second.At t=0 the area of the loop containing capacitor and the rod is zero and the capacitor is uncharged.The rod started moving at t=0 on the fixed smooth conducting rails which have negligible resistance.Find (i)The current in the circuit as a function of time t.
(ii)If the above system is kept in vertical plane such that the rod can move vertically downward due of gravity and other parts are kept fixed and B=constant =B0.then find the maximum current in the circuit.
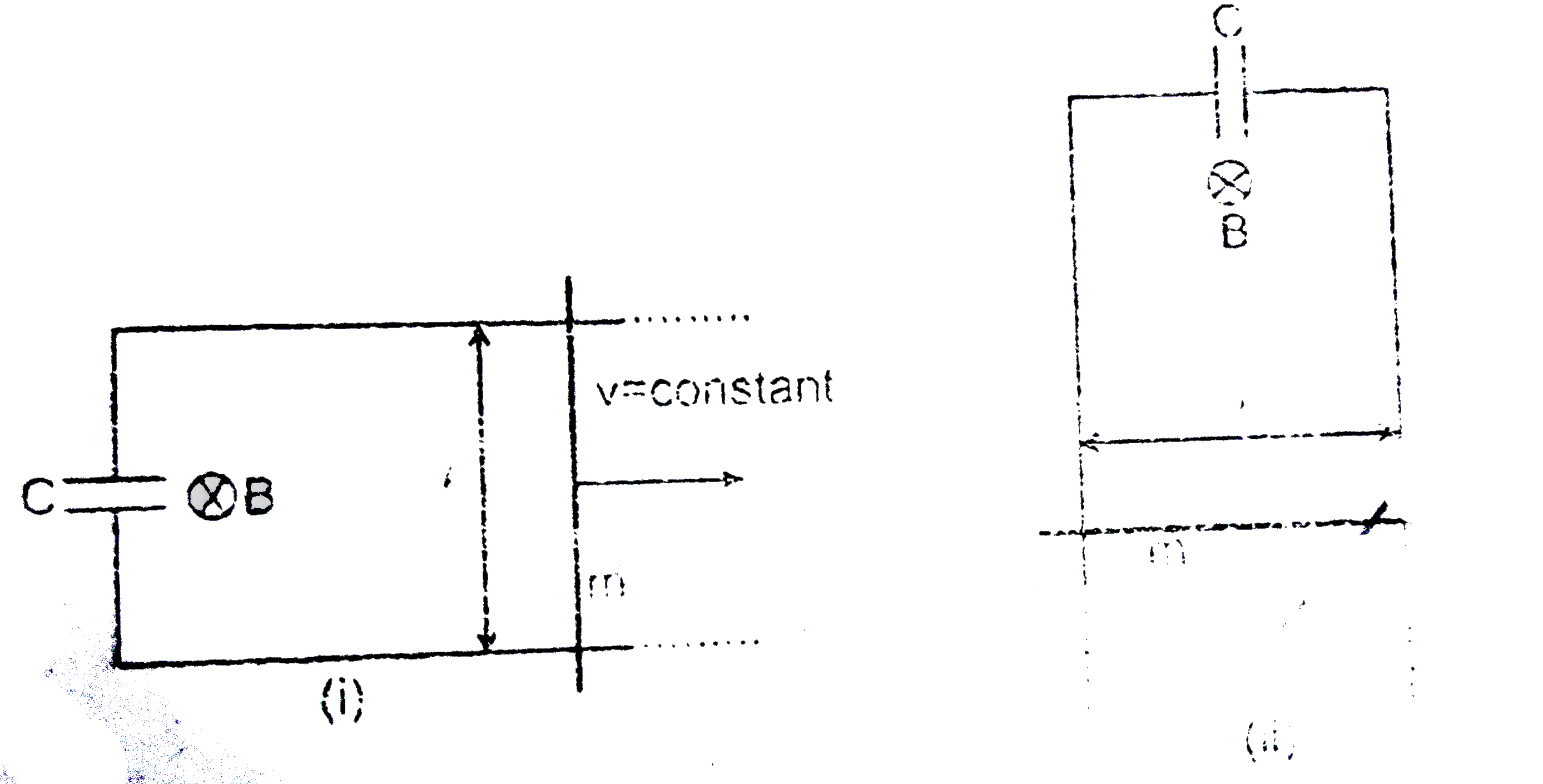
View SolutionIn the figure, a conducting rod of length l=1 meter and mass m=1kg moves with initial velocity u=5m/s. On a fixed horizontal frame containing inductor L=2H and resistance R=1W. PQ and MN are smooth, conducting wires. There is a uniform magnetic field of strength B=1T. Initially there is no current in the inductor. Find the total charge in coulomb, flown through the inductor by the time velocity of rod becomes vf=1m/s and the rod has travelled a distance x=3 meter.
View SolutionA pair of long conducting rails are held vertical at a separation l=50cm. The top ends are connected by a resistance of R=0.5Ω and a fuse (F) of negligible resistance. A conducting rod is free to slide along the rails under gravity. The whole system is in a uniform horizontal magnetic field B = 1.5 T as shown. Resistance of the rod and rails are negligible and the rod remains horizontal as it moves. The rod is released from rest. Find the minimum mass of the rod that will ensure that the fuse blows out. It is known that rating of the fuse is 4 A.
View SolutionA conducting rod of 1 m length and 1 kg mass is suspended by two vertical wires through its ends. An external magnetic field of 2T is applied normal to the rod. Now, the current to be passed through the rod so as to make the tension in the wires zero is : (Take g=10ms−2) :
View Solution