A flexible circular loop 20cm in diameter lies in a magneic field with magnitude 1.0T, direction lies into the plane of the page as shown in Fig. 3.187. The loop is pulled at the points indicated by the arrws, forming a loop of zero area in 0.314s.

The average induced emf in the circuit is
(a) 0.2V
(b) 0.1sV
( c) 1V
(d) 10V
The correct Answer is:B
(b)
εav=−ΔΦBΔt=−BΔAΔt=−B(−πr)2Δt
Since the flux through the loop is decreasing, the induced current must produce a field that goes into the page. Therefore, the current flows in clockwise direction
Iav=εavR=0.10.01=10A
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Integer
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Archives Fill In The Blanks
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A circular loop of area 1cm2 , carrying a current of 10 A , is placed in a magnetic field of 0.1 T perpendicular to the plane of the loop. The torque on the loop due to the magnetic field is
View SolutionA wire in the form of a circular loop of radius 10cm lies in a plane normal to a magnetic field of 100T. If this wire is pulled to take a square shape in the same plane in 0.1s, find the average induced emf in the loop.
View Solution
Knowledge Check
A flexible circular loop 20cm in diameter lies in a magneic field with magnitude 1.0T, direction lies into the plane of the page as shown in Fig. 3.187. The loop is pulled at the points indicated by the arrws, forming a loop of zero area in 0.314s.
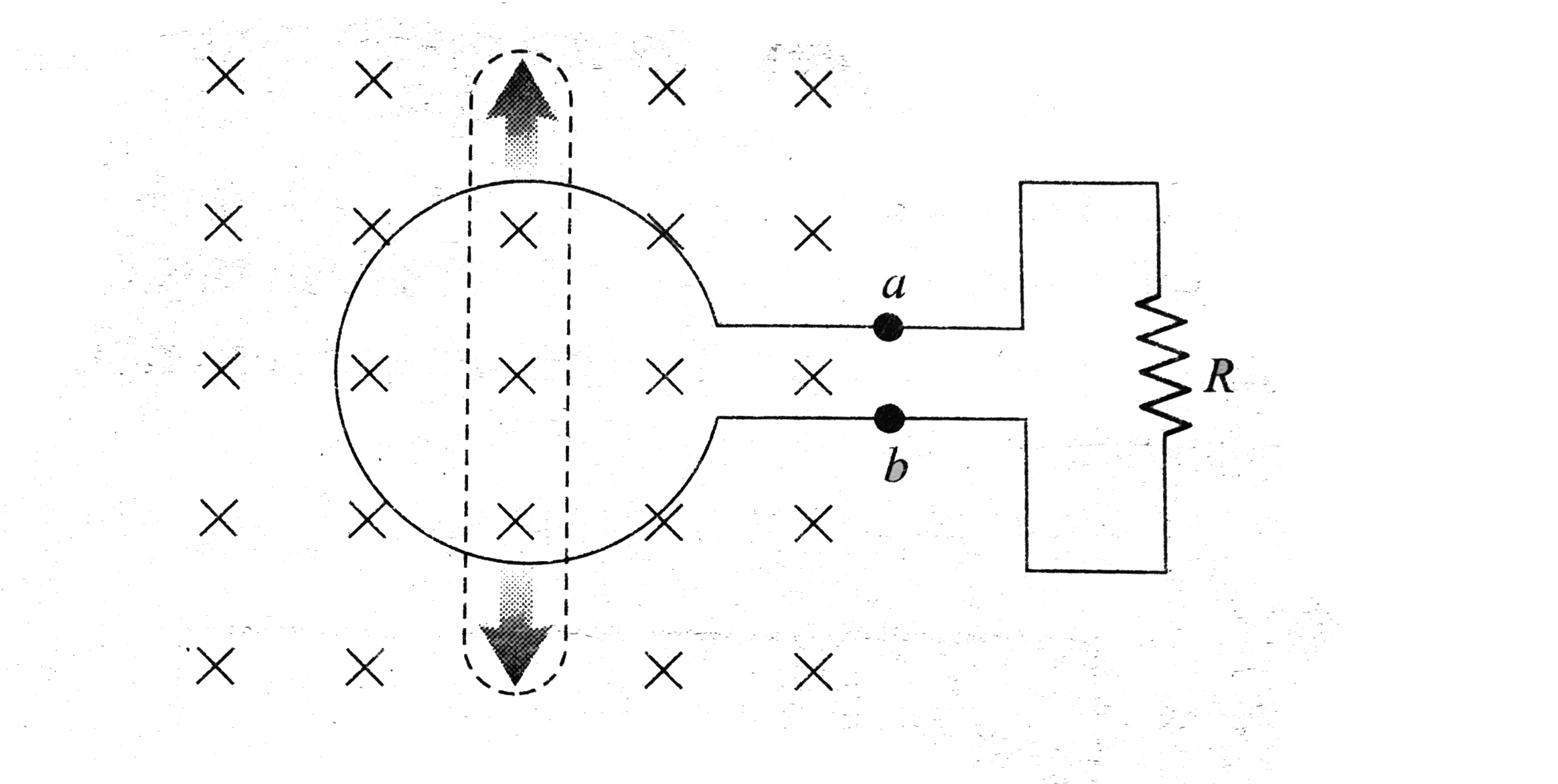
if R=0,01Ω, the magnitude and direction of current flowing in the loop areA(a) 1A, clockwiseB(b) 1A, anticlockwiseC( c) 10A, clockwiseD(d) 10A, anticlockwiseA circular coil of radius 2.00cm has 50 turns. A uniform magnetic field B=0.2T exists in the space in a direction parallel to the axis of rthe loop. The coil is now rotated about a diameter through an angle of 60∘ . The operation takes 0.Is . The average emf induced in the coil is
A6.28×10−2VB6.28×10−3VC62.8×10−2VD628×10−2VA loop shown in the figure is immersed in the varying magnetic field B=B0t, directed into the page. If the total resistance of the loop is R, then the direction and magnitude of induced current in the inner circle is
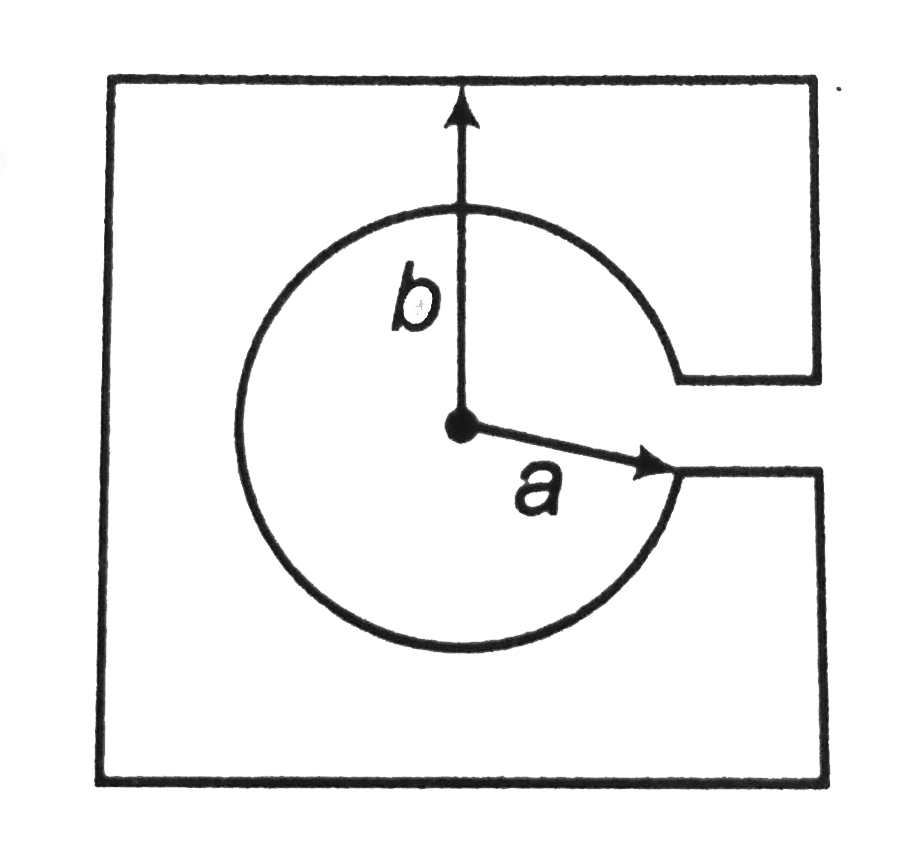 Aclockwise B0(πa2−b2)RBanticlockwise B0π(a2+b2)RCclockwise B0(πa2+4b2)RDclockwiseB0(4b2−πa2)R
Aclockwise B0(πa2−b2)RBanticlockwise B0π(a2+b2)RCclockwise B0(πa2+4b2)RDclockwiseB0(4b2−πa2)R
A loop of flexible conducting wire of length 0.5 m lies in a magnetic field of 1.0 T perpendicular to the plane of the loop. Show that when a current as shown in Fig. 1.112 is passed through the loop, it opens into a circle. Also calculate the tension developed in the wire if the current is 1.57 A.

View SolutionA conducting circular loop is placed in a magnetic field of strength 0.04 T, such that the plane of the loop is perpendicular to the magnetic field. If the radius of the loop begins to shrink at a constant rate of 0.5mm/s, then calculate the emf induced in the loop when its radius is 1.5 cm.
View SolutionA circular loop of radius R=20 cm is placed in a uniform magnetic field B=2T in xy-plane as shown in figure. The loop carries a current i=1.0A in the direction shown in figure. Find the magnitude of torque acting on the loop.

View SolutionA rectangular loop of sides 20cm and 10cm carries a current of 5.0A. A uniform magnetic field of magnitude 2T exists parallel to the longer side of the loop. The torque acting on the loop is
View SolutionA circular wire loop of radius r lies in a uniform magnetic field B, with its plane perpendicular to magnetic field. If the loop is deformed to a square shape in the same plane in time t, the emf induced in the loop is
View Solution
