Figure shows a conducting rod of length l=10cm, resistance R and mass m=100mg moving vertically downward due to gravity. Other parts are kept fixed. Magnetic filed is B=1T. MNandPQ are vertical, smooth, the capacitor is C=10mF. The rod is released from rest. Find the maximum current (in mA) in the circuit.
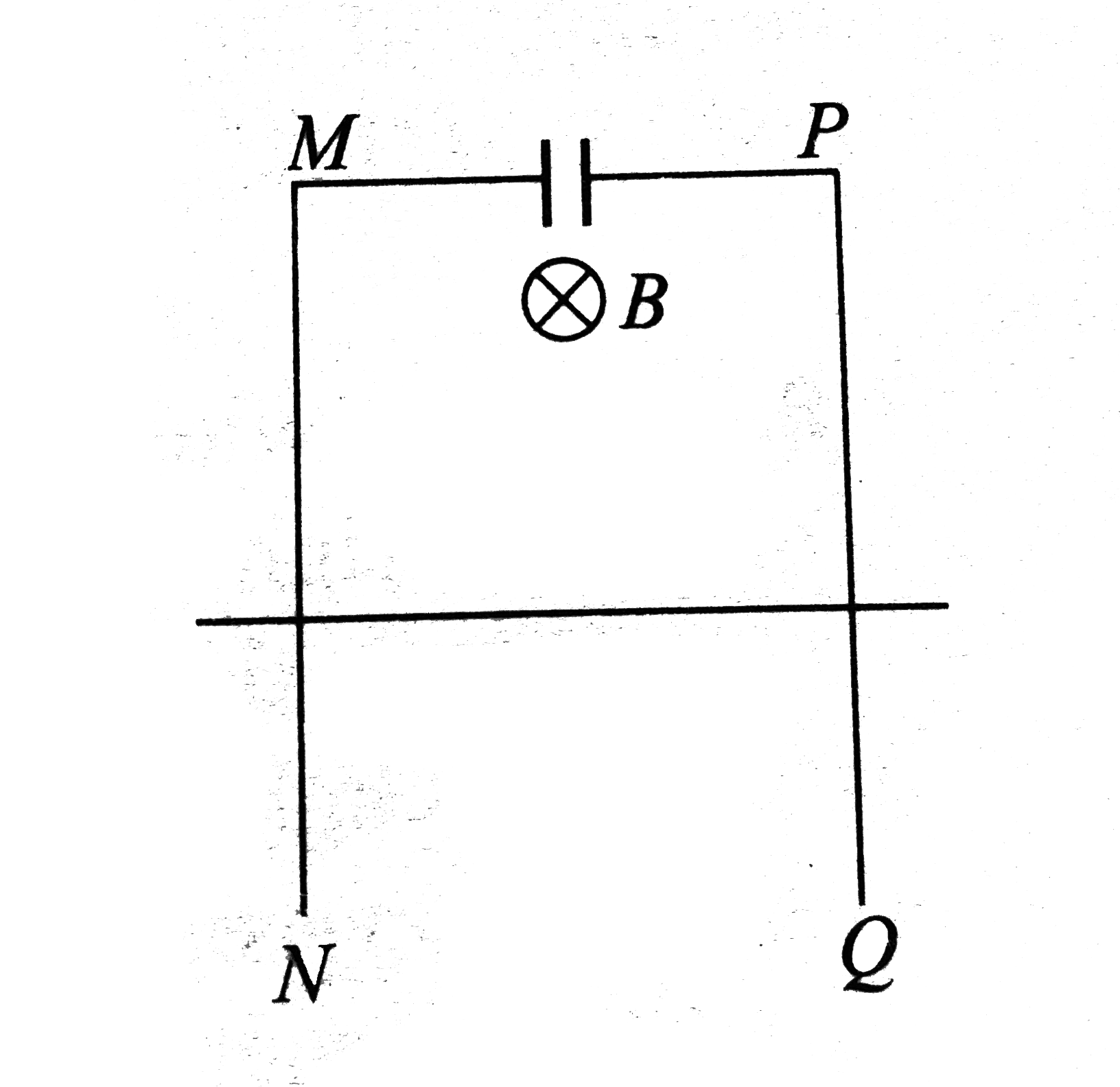
The correct Answer is:5
 ,
, 
By Newton's law, mg=ilB=mdvdt (i)
Using KVLblv=iR+qC
Differenting (ii) w.r.t. time, we get
Bldvdt=Rdidt+ic
Eliminating dvdt from equations (i) and (iii), we get
mg−ilB=mBl[Rdidt+iC]
→ mgBl−iB2l2=m(Rdidt+miC)
I will be maximum when dict=0. Use this in equation (iv)
→ mgBlC=i(B2l2C+m)
→ imax=mgBlCm+B2l2C
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Archives Fill In The Blanks
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Archives Single Correct
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Linked Comprehension
36 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
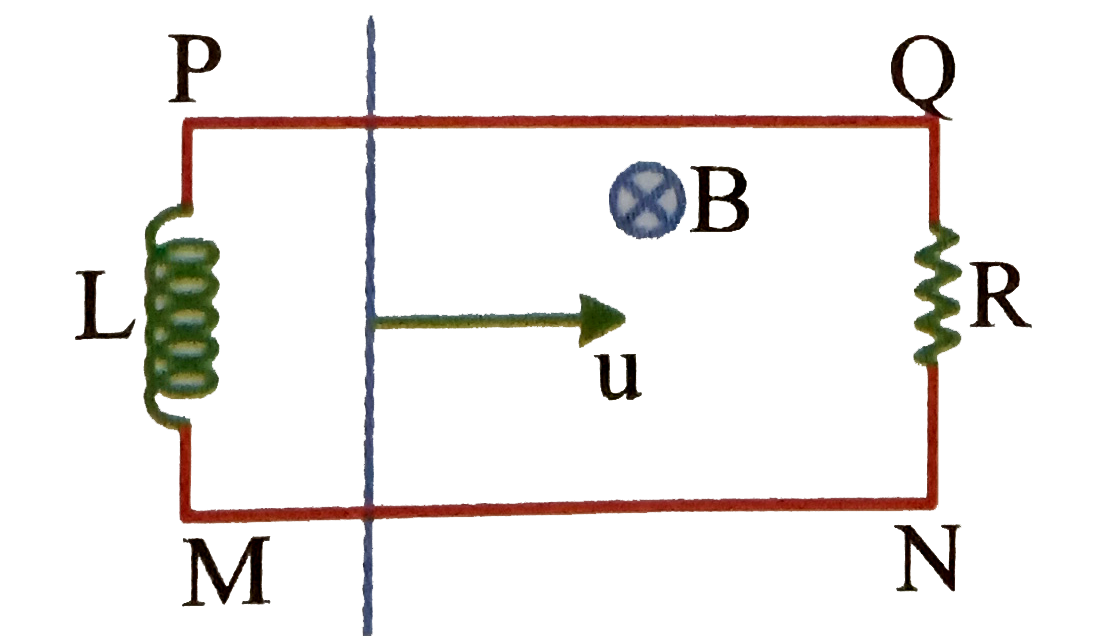
In the figure, a conducting rod of length l=1 meter and mass m=1kg moves with initial velocity u=5m/s. On a fixed horizontal frame containing inductor L=2H and resistance R=1W. PQ and MN are smooth, conducting wires. There is a uniform magnetic field of strength B=1T. Initial there is no current in the inductor. Find the total charge in coulomb, flown through the inductor by the time velocity of rod becomes vf=1m/s and the rod has travelled a distance x=3 meter.
View SolutionIn the figure shown a conducting rod of length l, resistnace R and mass m is moved with a constant velocity v.The magnetic field B varies with time t as B=5t, where t is time in second.At t=0 the area of the loop containing capacitor and the rod is zero and the capacitor is uncharged.The rod started moving at t=0 on the fixed smooth conducting rails which have negligible resistance.Find (i)The current in the circuit as a function of time t.
(ii)If the above system is kept in vertical plane such that the rod can move vertically downward due of gravity and other parts are kept fixed and B=constant =B0.then find the maximum current in the circuit.
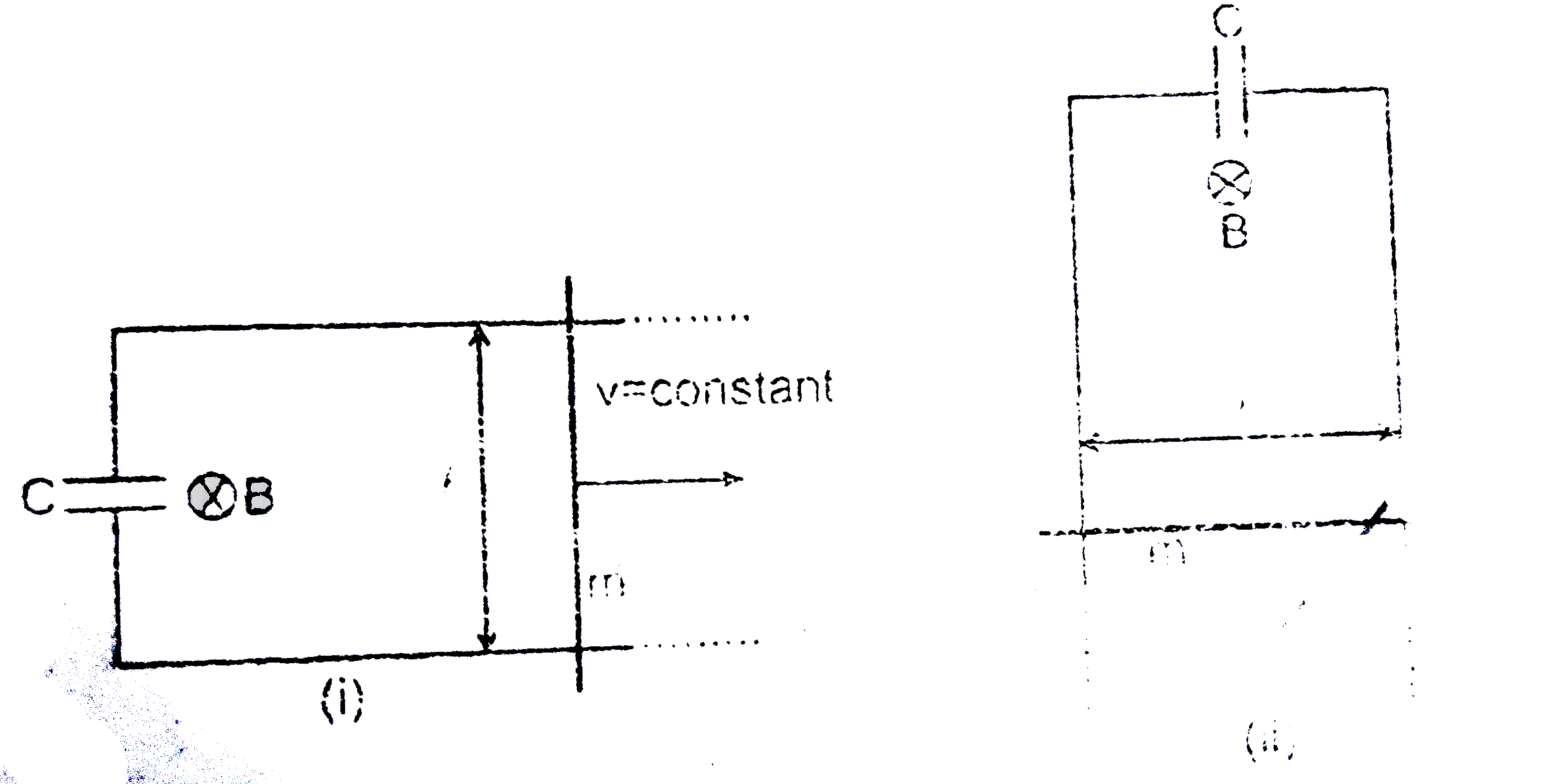
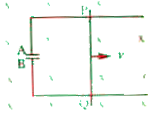
View SolutionA conducting rod of length L=0.1m is moving with a uniform sped v=0.2m/s on conducting raisli a magnetic field B=0.5T as shown. On one side, the end of the rails is connected to a capacitor of capacitance C=20μF. Then, the charge on the capacitor's plates are

View SolutionA conducting rod PQ of length L = 1.0m is moving with a uniform speed v = 2.0 m/s in a uniform B magnetic field B = 4.0 T directed into the paper. A capacitor of capacity C=10μF is connected as shown in the figure. Then what are the charges on the plates A and B of the capacitor
View SolutionA weightless rod of length 2l carries two equal masses 'm', one tied at lower end A and the other at the middle of the rod at B. The rod can rotate in vertical plane about a fixed horizontal axis passing thriugh C . The rod of is released from rest in horizontal possion. The speed of the mass B at the instant rod become vertical is:
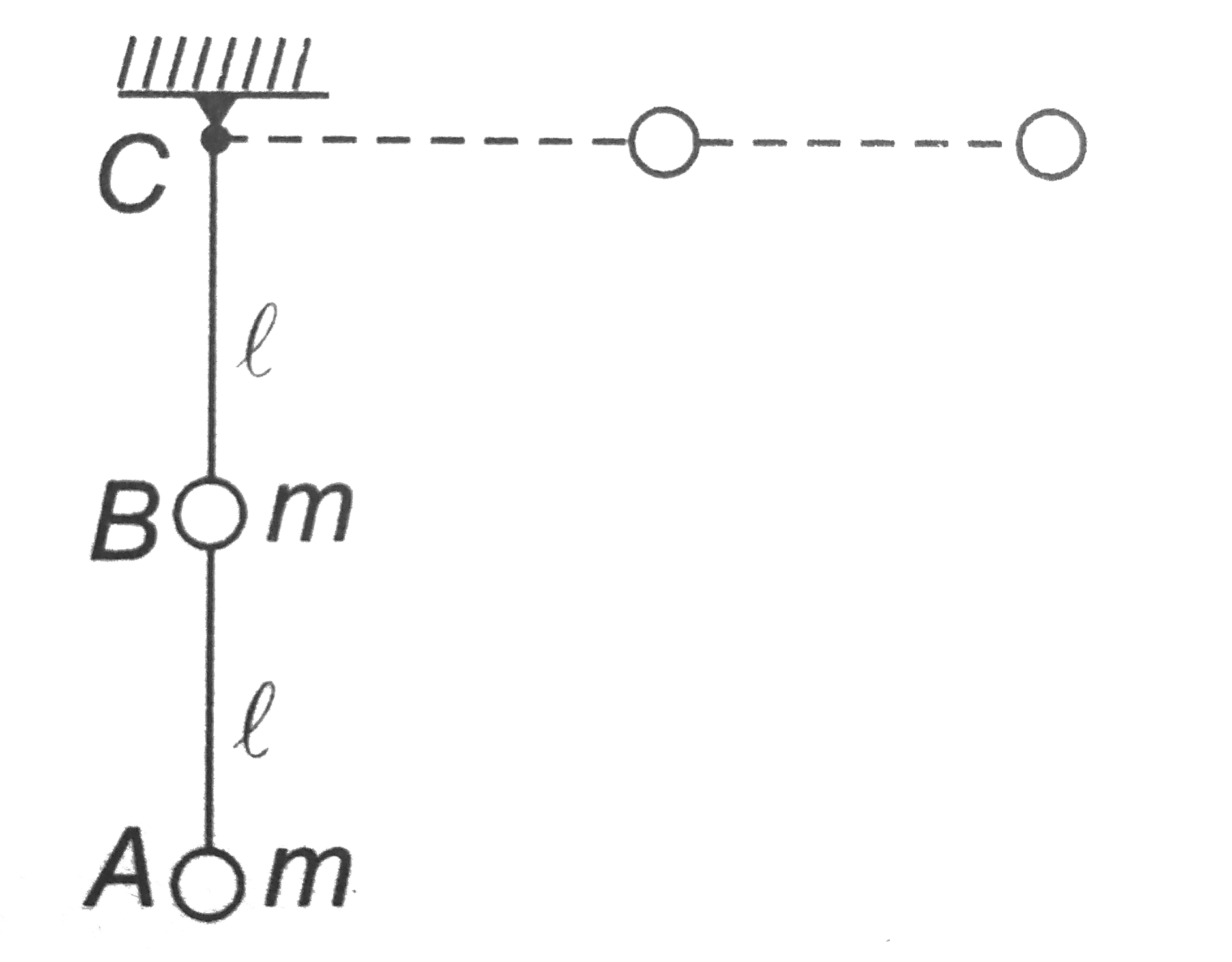
View SolutionA conducting ring of mass m and radius r has a weightless conducting rod PQ of length 2r and resistance 2R attached to it along its diametre. It is pivoted at its centre C with its plane vertical, and two blocks of mass m and 2m are suspended by means of a light inextensible string passing over it as shown in Fig. The ring is free to rotate about C and the system is placed in magnetic field B (into the plane of the ring). A circuit is now complete by connecting the ring at A and C to a battery of emf V. It is found that for certain value of V , the system remains static.

In static condition, find the current through rod PC.
View SolutionFigure shows a conducting rod of negligible resistance that can slide on smooth U-shaped rail made of wire of resistance 1Ω/m. Position of the conducting rod at t=0 is shown. A time dependent magnetic field B=2t tesla is switched on at t=0
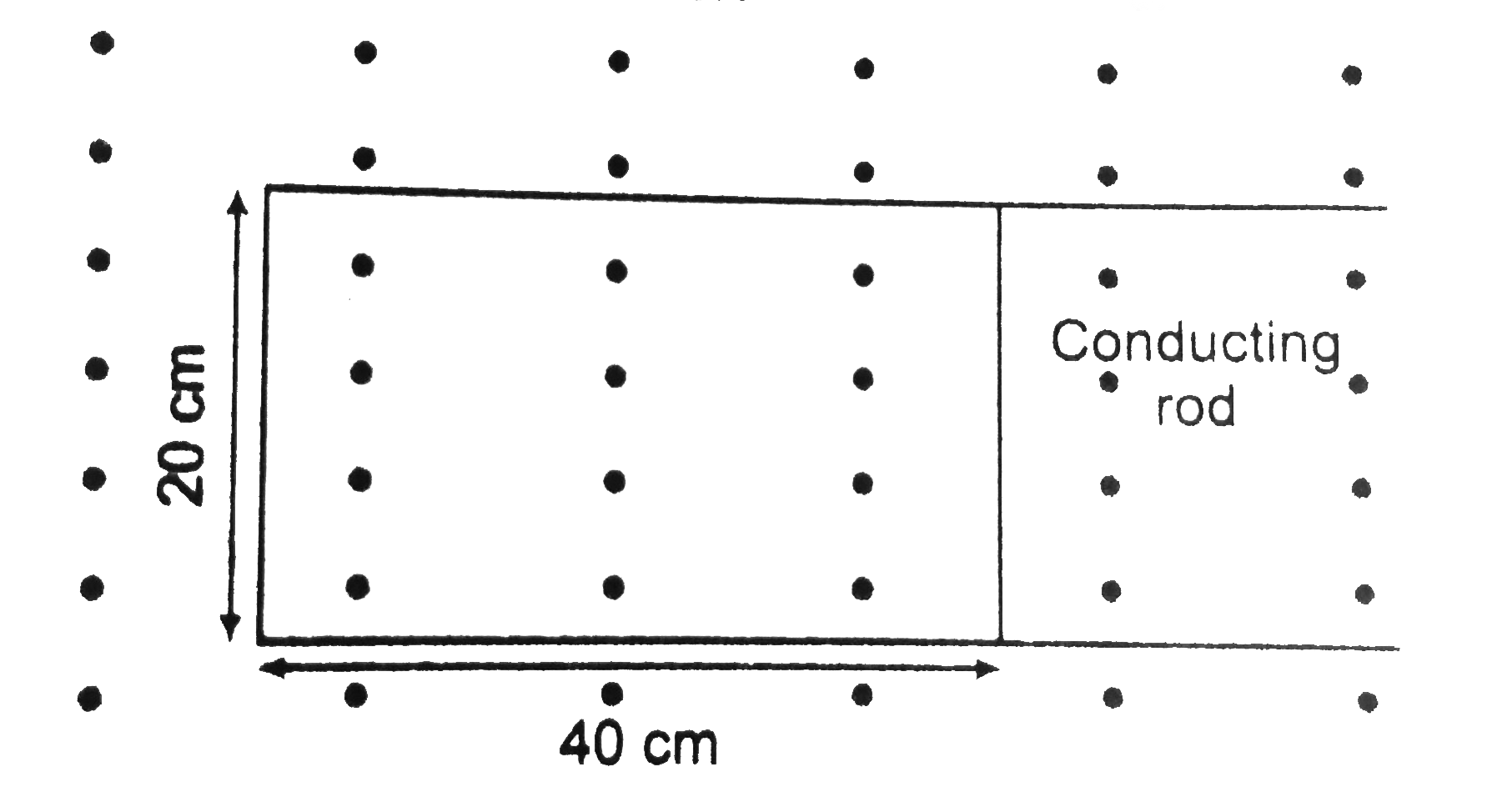
The current in the loop at t=0 due to induced emf is
View SolutionFigure shows a conducting rod of negligible resistance that can slide on smooth U-shaped rail made of wire of resistance 1Ω/m. Position of the conducting rod at t=0 is shown. A time dependent magnetic field B=2t tesla is switched on at t=0
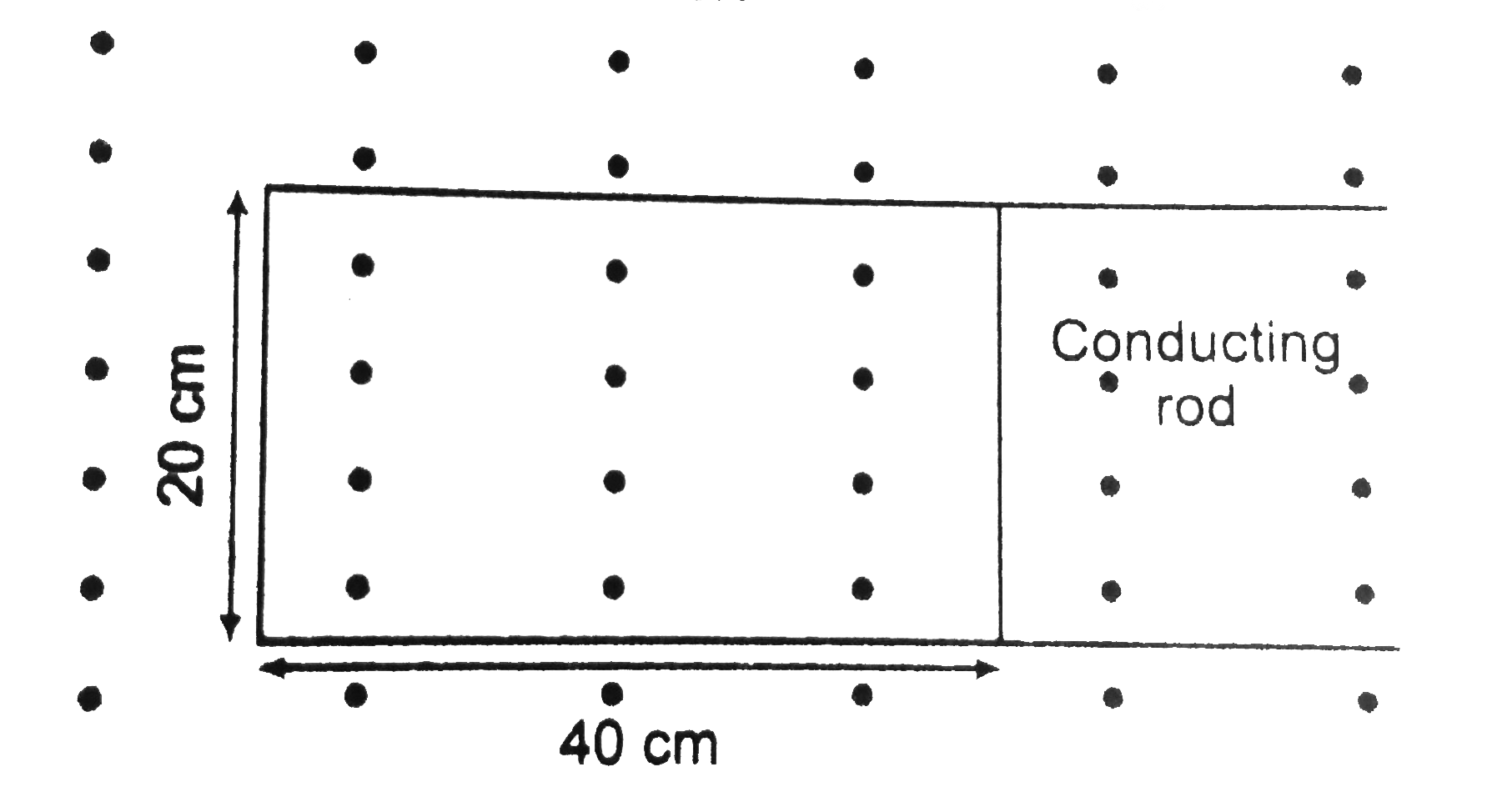
At t=0, when the magnetic field is switched on, the conducting rod is moved to the left at constant speed 5cm/s by some external means. At t=2s, net induced emf has magnitude
View SolutionA conducting rod PQ of length L=1.0m is moving with a uniform speed v=2.0ms−1 in a uniform magnetic field B=4.0T directed into the plane of the paper.
A capacitor of capacity C=10μF is connected as shown in , then

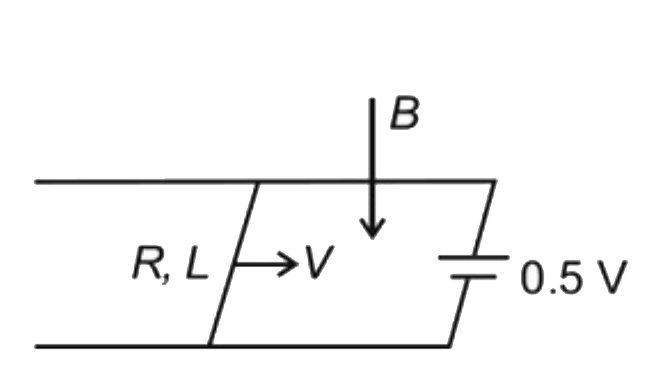
View SolutionThere is a pair of fixed, parallel rails of negligible resistance in a horizontal plane, at a distance of L = 10 cm. The rails are connected, at one of their ends to an ideal battery of EMF 0.5 V, as shown in the figure. The system is placed in a vertically downward and perpendicular magnetic field of magnetic induction B = 1T. A metal rod of resistance R=10Ω is placed perpendicularly on the rails. The rod placed perpendicularly on the rails. The rod and rails are frictionless. The magnitude of force, which is to be exerted on the rod in order to move it with a constant speed of order to move it with a constant speed of 1ms−1 in the direction shown, is
View Solution
