Figure shows a long straight wire of a circular cross - section (radius a) carrying steady current I. The current I is uniformly distributed across this cross - section . Calculate the magnetic field in the region r<a and r>a
 Solution in Tamil
Solution in Tamil
Consider the case r>a. The Amperian loop labelled 2, is a circle concentric with the cross -section . For this loop , L=2πr
Ie= Current enclosed by the loop = I We have B(2πr)=μ0
B=μ0I2πr
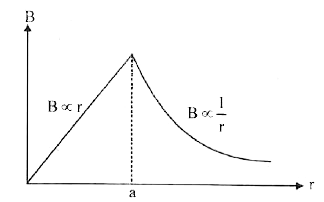
B∝1r(r>a)
b. Consider the case r<a . The amperian loop is a circle labelled 1. For this loop, taking the radius of the circle to be r, =2ir
Now the current enclosed Ie is not I, but is less than this value, Since the current distribution is uniform, the current enclosed is,
Ie=I(πr2πa2)=Ir2a2
Using Ampere.s law , B(2πr)=μ0Ir2a2
B=(μ0I2πa2)r
B∝r (r<a)
Figure shows a plot of the magnitude of B with distance r from the centre of the wire. The direction of the field is tangential to the respective circular loop (1 or 2) and given by the right-hand rule
Topper's Solved these Questions
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - SOLUTIONS TO EXERCISES FROM NCERT TEXT21videos
MOVING CHARGES AND MAGNETISM
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - PRACTICE PROBLEMS FOR SELF ASSESSMENT20videos
MOVING CHARGES AND MAGNETISM
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - COMPETITIVE EXAM CORNER13videos
MAGNETISM AND MATTER
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - NUCLEIEXERCISE - COMPETITIVE EXAM CORNER23videos
NUCLEI
Similar Questions
A cirular coil of wire cansiting of 100 turns ,each of readius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field ¯¯¯B at the centre of the coil ?
04:21View SolutionA vertical wire carries a current of 17 A. If the neutral point is observed at a distance of 10 cm from the wire, calculate the horizontal compoinent of earth's magnetic field .
04:54View SolutionChoose the correct statement .
09:31View SolutionRadioactive 6027Co is transformed into stable 6028Ni by emitting two γ - rays of energies
04:21View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.
 View Solution
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a
 02:52View Solution
02:52View SolutionFigure shows the circular cross-section of a long straight wire of radius a carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r lt a (dashed inner circle) and r gt a (dashed outer circle).
View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.
 03:43View Solution
03:43View SolutionThe adjoining figure shows a long straight wire of a circular cross section (radius a) carrying steady current I. The current I is uniformly distributed across its cross section. Calculate the magnetic field at a distance from its axis for (i) r lt a , (ii) r gt a .
09:15View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r a.
View SolutionA long straight wire of a circular cross-section (radius r) carries a steady current I. The current is distributed uniformly across the cross-section. Calculare the magnetic field at a point (a) outside the wire , (b) inside the wire. Draw a graph showing variation of magnetic field.
View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.
 03:22View Solution
03:22View SolutionA long straight wire of a curcular cross-section of radius 'a' carries a steady current 'l'. The current is uniformly distributed the across- section . Apply Amphere's circuital law to calculate the magnetic field at a point 'r' in the region for (i) r lt a and (ii) r gt a .
01:44View SolutionA long straight wire of radius 'a' carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetic fields at a/2 and 2a is
04:35View SolutionA long straight wire of radius 'a' carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetic fields at a/2 and 2a is
View Solution

