Figure shows a particle slideing on a frictionles track which terminates in straight horizontal section. If the particle starts slipping from the point. A, how far way from the track will the particle hit the ground ?
The correct Answer is:A, C, D
H=1m,h=0.5m
Applying law of conservation of Energy for point A and B
mgH=12mv2+mgh
→g−(12)v2=0.5g
→v2=2(g−0.5g)=g
→v=√g=3.1ms
After pointg B the body exhibits projectile motion for which
θ=0
y=−0.5
So, -0.5=4.9xxt^2<br>rarr t=0.31sec<br>So,x(v costheta)t<br>=3.1xx0.31=1m
So the practile will hit the ground at a horizontal distance m from B.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer16videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Objective -28videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer7videos
WAVE MOTION AND WAVES ON A STRING
Similar Questions
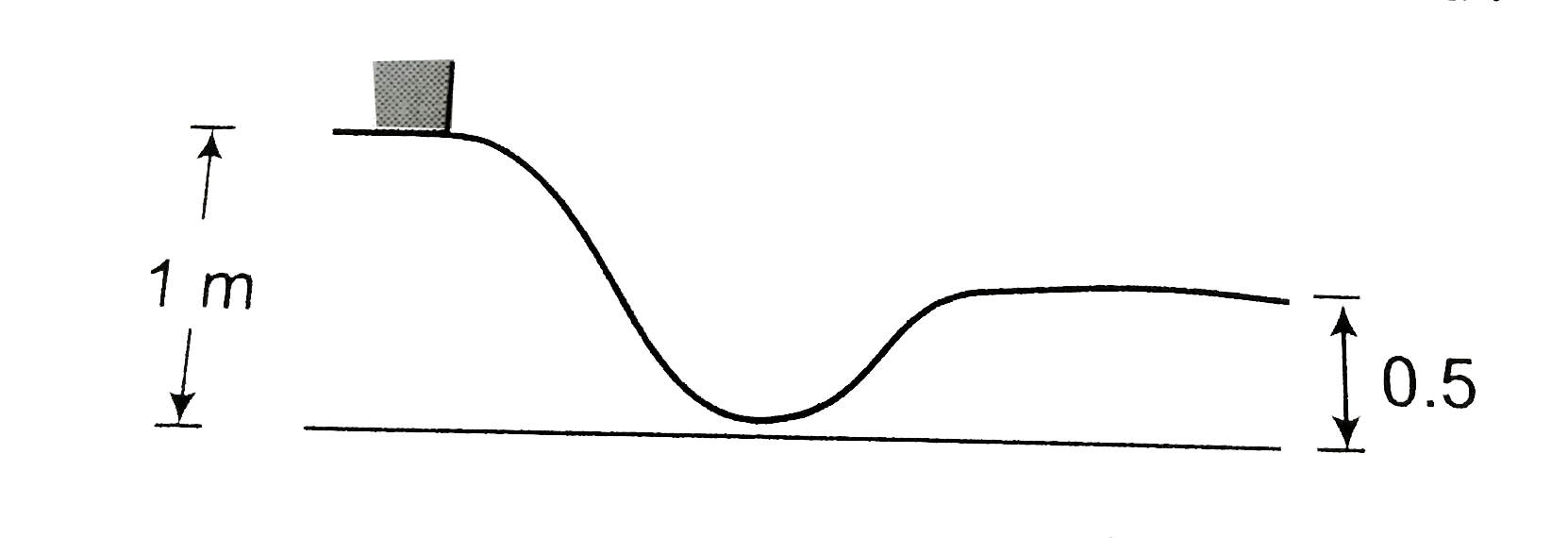
The figure shown a particle sliding on a frictionless track, which teminates in a straight horizontal section. If the particle starts slipping from the point A, how far away from the track will the particle hit the ground?View Solution
The figure shown a particle sliding on a frictionless track, which teminates in a straight horizontal section. If the particle starts slipping from the point A, how far away from the track will the particle hit the ground?View Solution
Knowledge Check
- Question 1 - Select One

The figure shown a particle sliding on a frictionless track, which teminates in a straight horizontal section. If the particle starts slipping from the point A, how far away from the track will the particle hit the ground?A1mB2mC3mD4m - Question 2 - Select One
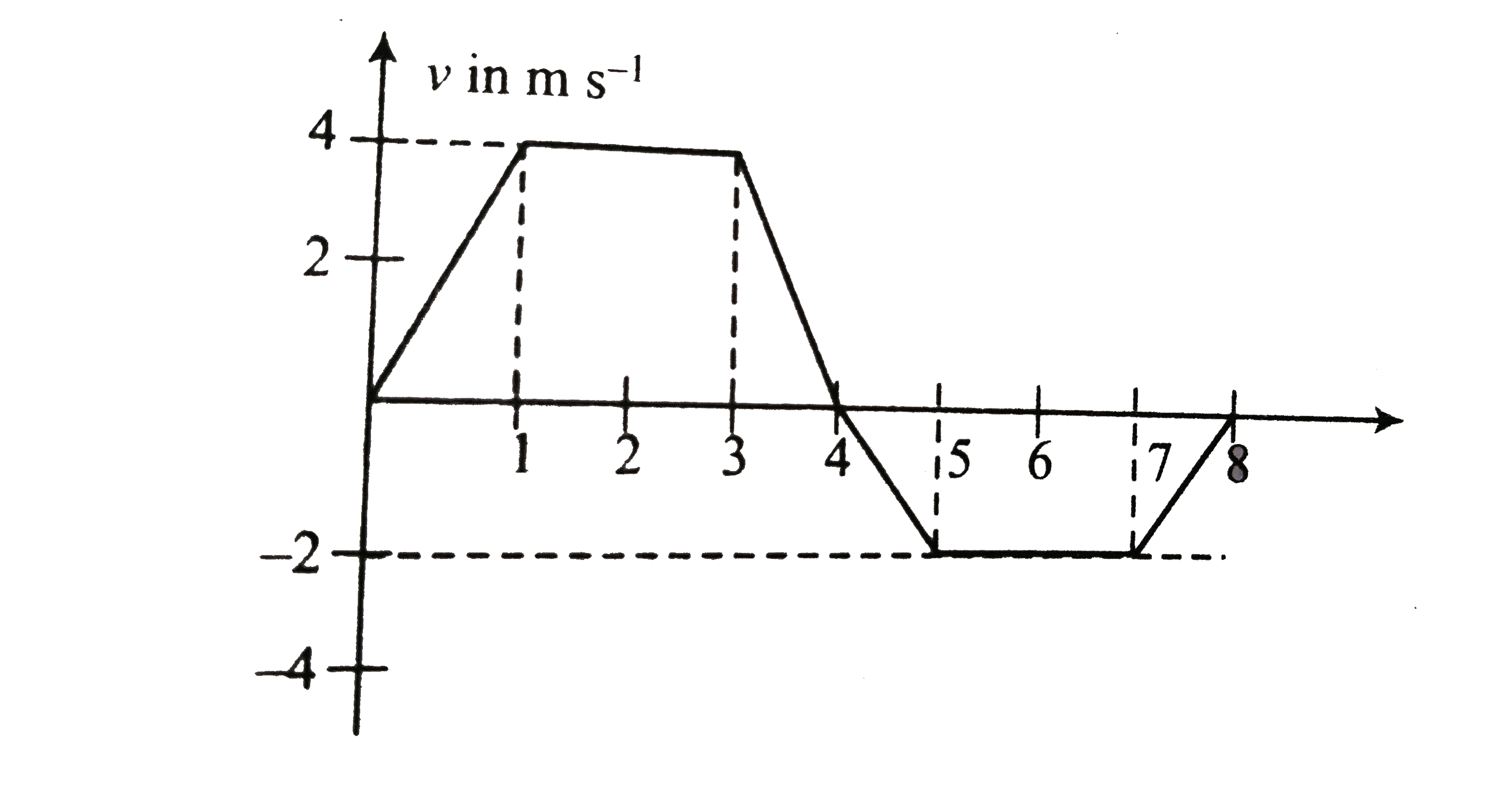
The velocity-time graph of a particle in straight line motion is veloity-time graph of a particle in straight line motion is shown in. The particle starts its motion from origin.
 .
.
The distance of the particle from the origin after 8s is .A18mB16mC8mD6m - Question 3 - Select One
A stone is just released from the window of a train moving along a horizontal straight track. The stone will hit the ground in
AStraight line pathBCircular pathCParabolic pathDHyperbolic path
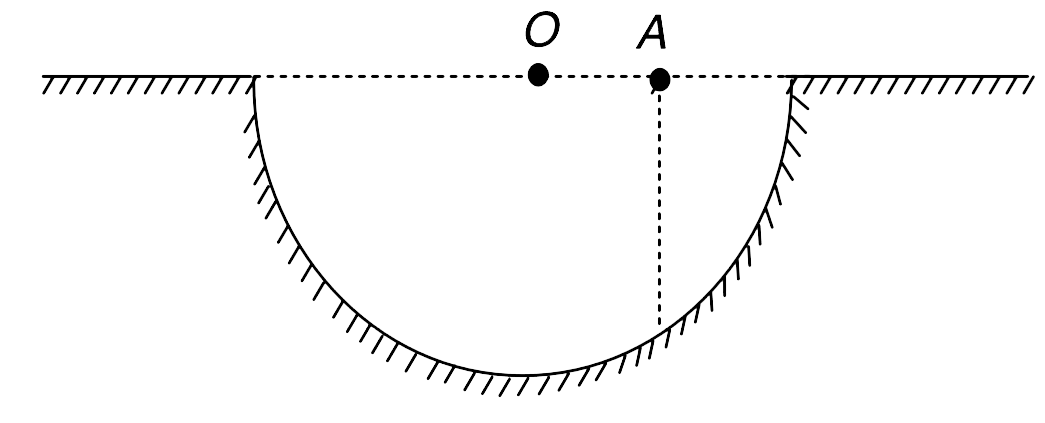
Figure shows a circular frictionless track of radius R, centred at point O. A particle of mass M is released from point A(OA=R/2). After collision with the track, the particle moves along the track.
(a) Find the coefficient of restitution e.
(b) What will be value of e if the velocity of the particle becomes horizontal just after collision ?
 View Solution
View SolutionThe velocity-time graph of a particle in straight line motion is velocity-time graph of a particle in straight line motion is shown in. The particle starts its motion from origin.
 .
.
The distance of the particle from the origin after 8s is .View SolutionA stone is just released from the window of a train moving along a horizontal straight track. The stone will hit the ground in
View SolutionFigure shows a circular frications trck of radius R, centred at point O. A particle of mass M is released from point A(OA=R/2). After collision with the track, the particle moves along on the track. Then the coefficient of restitution e is.
 View Solution
View SolutionFigure shows a circular frications trck of radius R, centred at point O. A particle of mass M is released from point A(OA=R/2). After collision with the track, the particle moves along on the track. Then the coefficient of restitution e is.
 View Solution
View Solution

