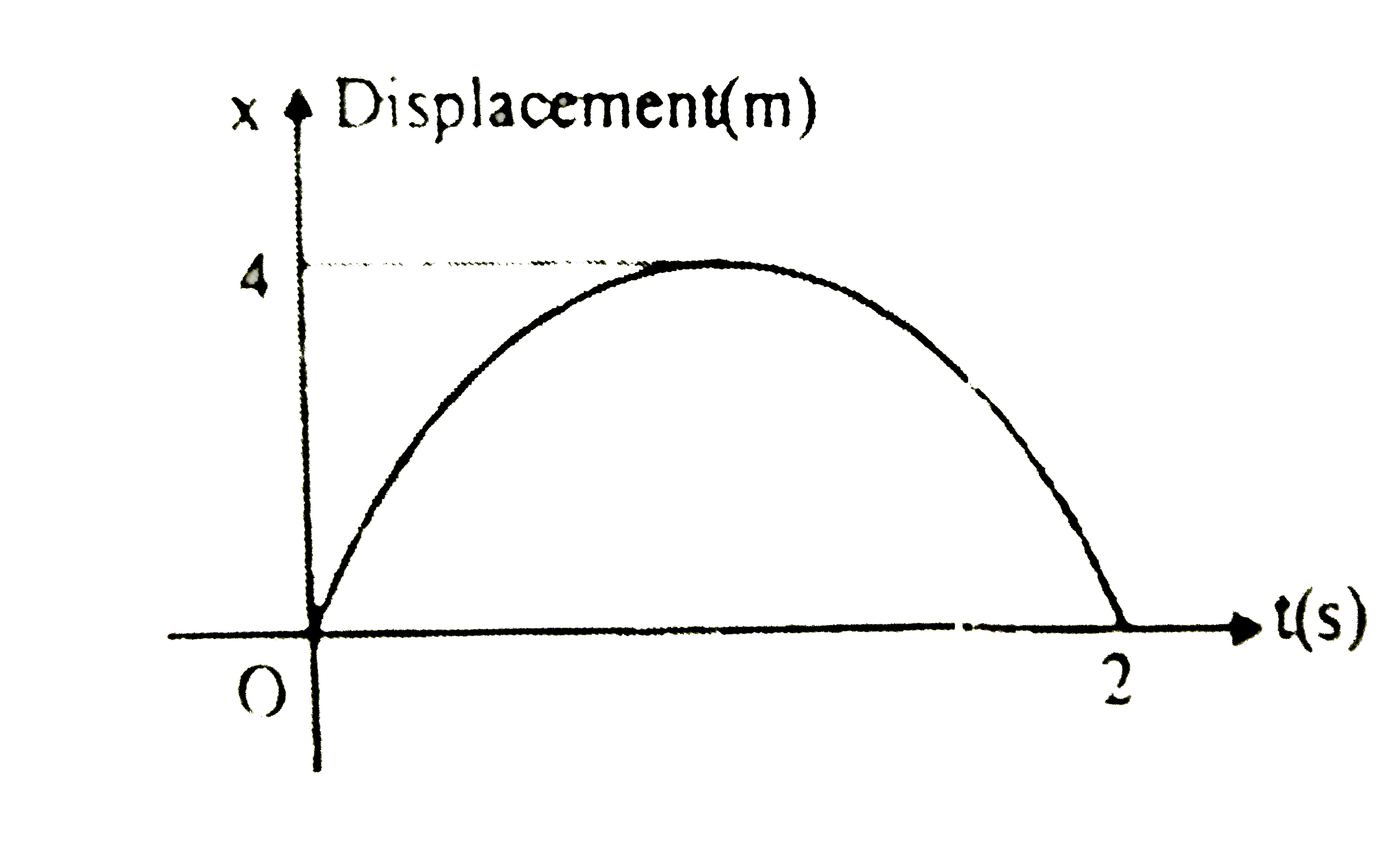
Figure shows a sine curve, as the displacement time curve of a particle executing rectilinear motion having equation x=45(π2t). The velocit of particle at t=23s is
 Solution in Gujrati
Solution in Gujrati
πms−1
√3πms−1
π2ms−1
None of these
Step by step video & image solution for Figure shows a sine curve, as the displacement time curve of a particle executing rectilinear motion having equation x = 45 ((pi)/(2)t). The velocit of particle at t = (2)/(3)s is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - RACEEXERCISE - Race 215videos
RACE
- BOOK - ALLEN CHAPTER - RACEEXERCISE - PHYSICS12videos
RACE
- BOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
- BOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example1videos
SIMPLE HARMONIC MOTION
Similar Questions
Two projectiles are projected with velocity vA,vB at angles θA (from horizontal) and θB (from vertical) as shown in the figure below, such that vA>vB but having same horizontal component of velocity. Which of the following is correct ?
 02:29View Solution
02:29View SolutionThe graph shown the extension of is wire of length 1 m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm2, then the Young's modulus of the material of the wire.
 02:26View Solution
02:26View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
02:20View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.02:48View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
01:25View SolutionA particle is executing a motion in which its displacement as a function of time is given by x = 3 sin (5 pi t + pi//3) + cos (5pi + pi//3) where x is in m and t is in s . Then the motion is
06:18View SolutionA particle executes simple harmonic motion according to the displacement equation y=10cos(2πt+π6)cm where t is in second The velocity of the particle at t=16 second will be
02:57View SolutionDisplacement time equation of a particle executing SHM is, x = 10 sin ((pi)/(3)t+(pi)/(6))cm . The distance covered by particle in 3s is
04:19View SolutionThe force-time(F–t) curve of a particle executing linear motion is as shown in the figure. The momentum acquired by the particle in time interval from zero to 8 second will be
 03:13View Solution
03:13View SolutionFigure shows a sine curve, as the displacement time curve of a particle executing rectilinear motion having equation x = 45 ((pi)/(2)t) . The velocit of particle at t = (2)/(3)s is
04:14View SolutionThe following figure shows displacement versus time curve for a particle executing simple harmonic motion :

Which one of the following statements is correct?05:37View SolutionDisplacement of a particle executing SHM s x= 10 ( cos pi t + sin pi t) . Its maximum speed is
View SolutionThe displacement of a particle executing SHM is given by. y=5 sin(4t+pi/3) If T is the time period and the mass of the particle is 2 g, the kinetic energy of the particle when t=T/4 is given by,
04:17View Solutionसरल आवर्त गति कर रहे एक कण का विस्थापन (x) समीकरण x=Acosωt द्वारा प्रदर्शित है। निम्न में से किस रेखाचित्र द्वारा कण की स्थितिज ऊर्जा (PE) , विस्थापन (x) तथा समय ( t ) के पदों में प्रदर्शित होगी ?
 01:40View Solution
01:40View SolutionThe displacement equation of a particle executing S.H.M is given by y=0.01sinπ(t+0.005)m. Calculate the maximum velocity and displacement at the time of start of the motion.
01:12View SolutionThe displacement x of a particle in rectilinear motion at time t is represented as x2=at2+2bt+c, where a ,b, and c are constants. Show that the acceleration of this particle varies 1x3.
View Solution

