Figure shows a stream of fluid emerging from a tube in the base of an open tank. Obtain an expression for 'y' in terms of θ and 'h'. Can exceed 'h'?

We apply Bernoullis equation between points 2 and 3.
P2+12ρv22+ρgy2=P3+12ρv23+ρgh3
Patm+12ρv22+0=Patm+12ρv23+ρgy………i
As both the points are open the atmosphere P2=P3=Patm
Taking ground level as reference level potential energy at point 2 is zero.
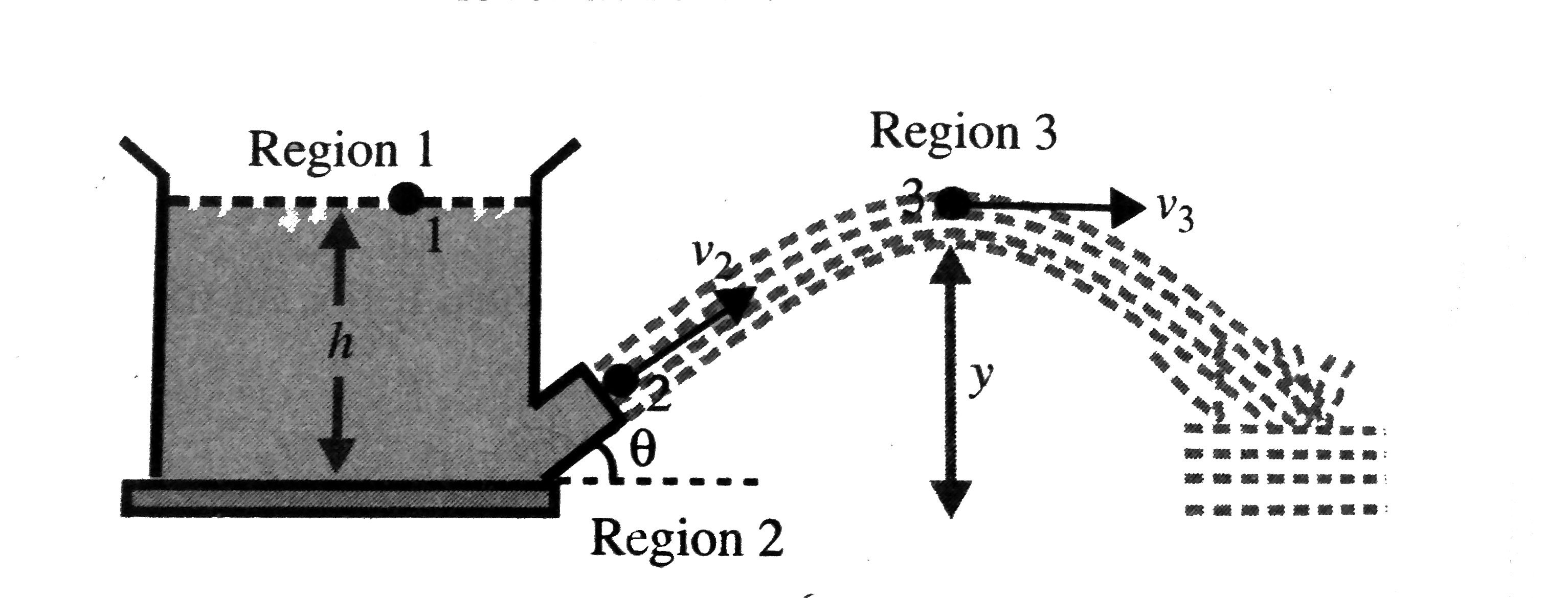
Since there is no horizontal acceleration v3=v2cosθ.
From eqn i we obtain
y=12(v22−v22cos2θ)g=12v22sin2θg....ii
From Torricelli's theroem v22=2gh
That, y=sin2θ
y=h when sinθ=1, i.e. θ=90∘ therefore y can never exceed h.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Subjective25videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Single Correct95videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.310videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
The nature of a solution can be expressed in terms of its [H3O+]. Explain.
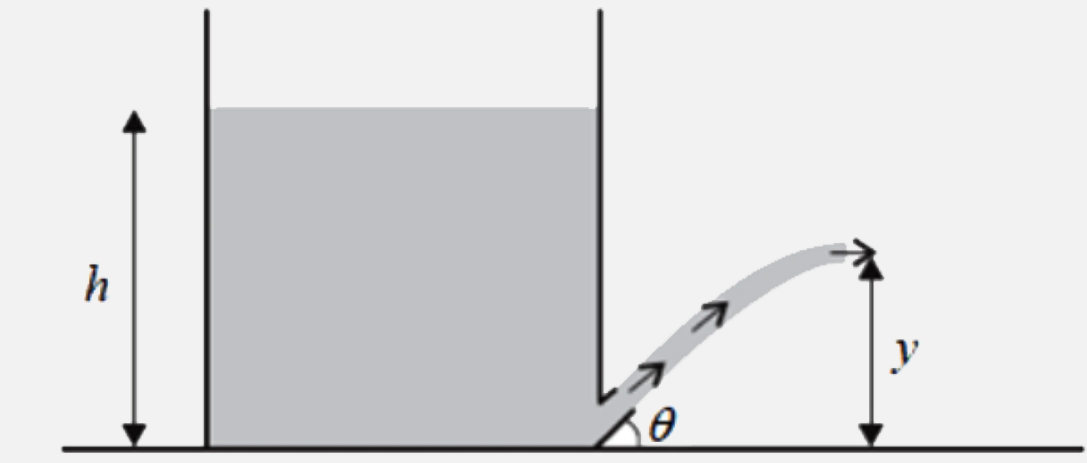
View SolutionA stream of non-viscous liquid emerges from a very short outlet tube at the base of a large . Open tank , in which the depth of liquid is h. The tube is at a fixed angle θ to the ground as shown in the figure. The maximum height of the stream y is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Figure shows how the stream of water emerging from a faucet necks donw as it falls. The area changes from A0 to A through a fall of h. At what rate does the water flow from the tap ?
 AA0√2ghA2A20−A2B2A0√ghA2A20−A2CA0√gh2D2A ⎷ghA20A20−A2
AA0√2ghA2A20−A2B2A0√ghA2A20−A2CA0√gh2D2A ⎷ghA20A20−A2 - Question 2 - Select One
The height of the water in a tank is H. The range of the liquid emerging out from a hole in the wall of the tank at a depth 3H4 from the upper surface of water, will be
AHBH2C3H2D√3H2 - Question 3 - Select One
Figure shows a capillary rise H. If the air is blown through the horizontal tube in the direction as shown then rise in capillary tube will be
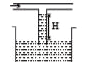 A=HB>HC<HDzero
A=HB>HC<HDzero
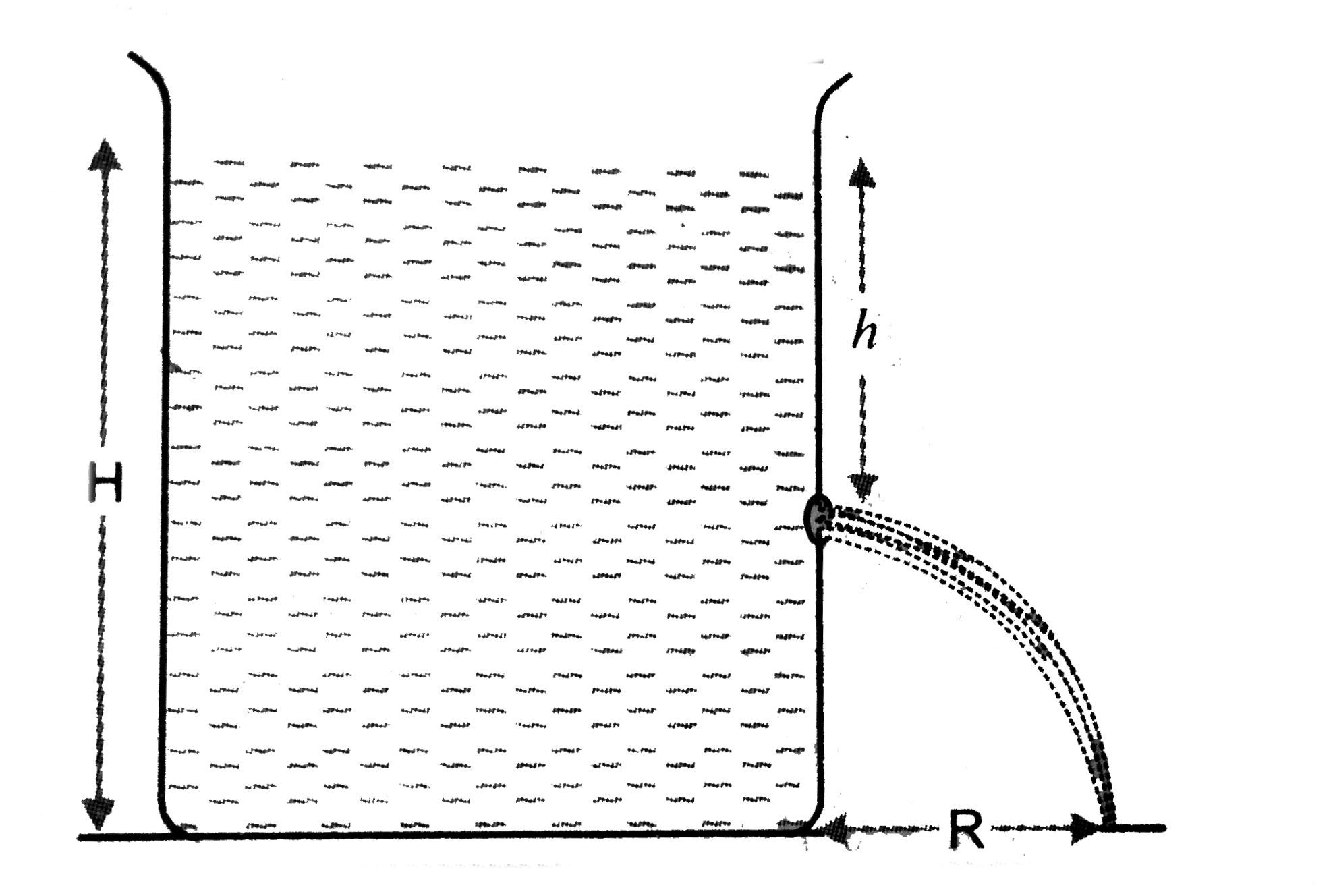
Water stand at a heigh H in a tank whose sides are vertical. An orifice is made at the depth h on one of the wall Fig. 7(c).25. The emerging stream of water strikes at the distance R from the tank on the floor./ Find the relation for R in term of h, and H. When R is maxmimum, how h and H are related.
 View Solution
View SolutionA horizontal stream of water leaves an opening in the side of a tank. If the opening is h metre above the ground and the stream hits the round D metre away, then what is the speed of water as it leaves the tank in terms of g, h and D ?
View SolutionFigure shows a device called Pitot tube . It measures the velocity of moving fluids . Determine the velocity of the fluid in terms of the density ρ the density of the fluid in manometer (U-tube) σ and the height h .
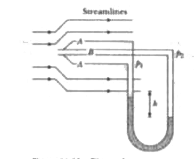 View Solution
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external forceView SolutionA wooden cylindrical of diameter 4r, height h and density ρ/3 is kept on a hole of diameter 2r of a tank , filled with water of density ρ as shown in the figure . The height of the base of cylinder from the base of tank is H .
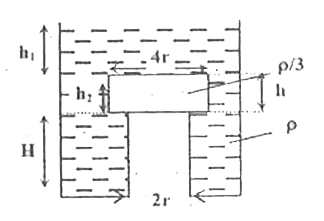
Let the cylinder is prevented from moving up , by applying a force and water level is further decreased . Then , height of water level (h2 in figure ) for which the cylinder remains in original position without application of force isView Solution

