Figure shows a device called Pitot tube . It measures the velocity of moving fluids . Determine the velocity of the fluid in terms of the density $ρ$ the density of the fluid in manometer (U-tube) $σ$ and the height h .

Text Solution

Verified by Experts

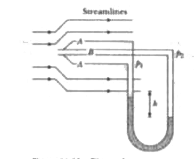
The fluid inside the right tube must be at rest as the fluid exactly at the end is in contact with the fluid in Pitot tube , which is at rest .
The velocity $v_{1}$ is the fluid velocity $v_{f}$ . The velocity $v_{2}$ of the fluid at point B is zero and the pressure in the right arm is $p_{2}$ (called stagnation pressure ) .
Thus , using Bernoulli.s principle
$ρ_{1} + \frac{1}{2} ρ v_{1}^{2} = p_{2} + \frac{1}{2} ρ v_{2}$
we get $ρ_{2} = p_{1} + \frac{1}{2} ρ v_{f}^{2}$
On the other hand , the openings at point A is not along the flow lines , so we do not need to use Bernoulli.s equation . We can simply say that the pressure just outside the opening is same as that within the Pitot tube .
Therefore , the pressure at the left arm of the manometer is same as the fluid pressure $p_{f}$ , that is $p_{1} = p_{f}$ .
Also $p_{2} = p_{1} + (ρ - σ) g h (14 - 54)$
Generally , $σ < < ρ$ , so it is ignored .
Thus , $p_{2} = p_{f} + ρ g h (14 - 55)$
From Eqs. 14-54 and 14-55
$\frac{1}{2} σ v_{f}^{2} = ρ g h$
or $v_{f} = \sqrt{\frac{2 ρ g h}{σ}}$

Updated on:21/07/2023

In laminar flow of fluid, the velocity of the fluid in contact with the walls of the tube is
Amaximum
Bbetween $0$ and maximum
Cequal to critical velocity
Dzero
If rho is density of falling body and sigma is the density of fluid then the terminal velocity of the falling body is proportional to
A $(ρ - σ)$
B $\frac{ρ}{σ}$
C $ρ σ$
D $(π + σ)$
A fluid is flowing through a tube of length L. The radius of the tube is r and the velocity of the fluid is v. If the radius of the tube is increased to 2r, then what will be the new velocity?
A4v
Bv/4
Cv/2
D2v