Figure shows a student, again sitting on a stool that can rotate freely about a vertical axis. The student, initially at rest, is holding a bicycle wheel whose rim is loaded with lead and whose rotational inertia $I_{w h}$ about its central axis is $1.2 k g \cdot m^{2}$ .
The wheel is rotating at an angular speed $ω_{w h}$ of 3.9 rev/s, as seen from overhead, the rotation is counterclockwise. The axis of the wheel is vertical, and the angular Momentum ${\to L}_{w h}$ of the wheel points vertically upward.

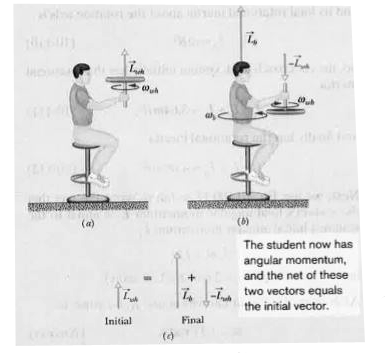
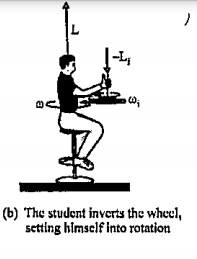
The student now inverts the wheel so that, as seen from overhead, it is rotating clockwise. Its angular momentum is now $- {\to L}_{w h}$ . The inversion results in the student, the stool, and the wheel's center rotating together as a composite rigid body about the stool's rotation axis, with rotational inertia $I_{b} = 6.8 k g \cdot m^{2}$ . With what angular speed $ω_{b}$ and in what direction does the composite body rotate after the inversion of the wheel?

Text Solution

Verified by Experts

1. The angular speed $ω_{b}$ we seek is related to the final angular momentum ${\to L}_{b}$ of the composite body about the stool.s rotation axis by $(L = I ω)$ .
2. The initial angular speed $ω_{w h}$ of the wheel is related to the angular momentum ${\to L}_{w h}$ of the wheel.s rotation about its center by the same equation.
3. The vector addition of ${\to L}_{b} and {\to L}_{w h}$ gives the total angular momentum $L_{tot}$ of the system of the student, stool, and wheel.
4. As the wheel is inverted, no net external torque acts on that system to change ${\to L}_{tot}$ about any vertical axis. So, the system.s total angular momentum is conserved about any vertical axis, including the rotation axis through the stool.
Calculations: The conservation of ${\to L}_{tot}$ is represented with vectors in Fig. We can also write this conservation in terms of components along a vertical axis as
$L_{b f} + L_{w h . f} = L_{b, i} + L_{w h, i}$ .
Where i and f refer to the initial state and the final state. Because inversion of the wheel inverted the angular momentum vector of the wheel.s rotation, we substitute $- L_{w h, i} for L_{w h, f}$ . Then, if we set $L_{b, i} = 0$ .
$L_{b, f} = 2 L_{w h, i}$ .
Using Equation, we next substitute $I_{b} ω_{b} for L_{b . f} and I_{w h} ω_{w h} for L_{w h, i}$ and solve for $ω_{b}$ , finding
$ω_{b} = \frac{2 I_{w h}}{I_{b}} ω_{w h}$
= $\frac{(2) (1.2 k g \cdot m^{2}) (3.9 r e v / s)}{6.8 k g \cdot m^{2}} = 1.4 r e v / s$ .

Updated on:21/07/2023

A wheel is rotating freely at an angular speed of 800 rev/min on a shaft whose rotational inertia is negligible. A second wheel initially at rest with thrice the rotational inertia of the first is suddenly coupled to the same shaft. The fraction of original kinetic energy lost is
A $\frac{2}{3}$
B $\frac{1}{3}$
C $\frac{1}{4}$
D $\frac{1}{2}$
Kinetic energy of a wheel rotating about its central axis is E. Then kinetic energy of another axis is E. Then kinetic energy of another wheel having twice the moment of inertia and half the angular momentum as that of the first wheel is
A8 E
B4 E
CE/8
DE/4