Figure shows a vertical force applied tangentially to a uniform cylinder of weight Fg. The coefficient of static friction between the cylinder and all surfaces is 0.500. In terms of Fg , find the maximum force P that can be applied that does not cause the cylinder to rotate.

When it is on the verge of slipping, the cylinder is in equilibrium.
∑Fx=0f1=n2μsn1 and f2=μsn2
∑Fy=0P+n1+f2=FS
∑τ=0P=f1+f2
As P grows so do f1 and f2
therefore since μs=12,f1=n12 and f2=n22=n14
then P+n1=n14=Fg
p=n12+n14=34n1
so P+54n1=Fg
becomes P=54(43)=Fg or 83P=Fg

Therefore P=38Fg
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.4
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.2
17 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A uniform cylinder rests on a cart as shown. The coefficient of static friction between the cylinder and the cart is 0.5 If the cylinder is 4cm in diameter and 10cm in height, which of the following is the minimum acceleration of the cart needed to cause the cylinder to tip over ?
 .
.
View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View Solution
Knowledge Check
The coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?
 A0.15mgB0.05mgC0.1mgD0.45mg
A0.15mgB0.05mgC0.1mgD0.45mg
If the coefficient of friction between all surface figure is 0.4 then find the minimum force F to have equilibrium of the system.

View SolutionA force F is applied on the top of a cube as shown in the figure. The coefficient of friction between the cube and the ground is μ. If F is gradually increased, find the value of μ for which the cube will topple before sliding.

View SolutionA force F is applied at the centre of a disc of mass M. The minimum value of coefficient of friction of the surface for rolling is
View SolutionA solid sphere of mass 0.50 kg is kept on a horizontal surface. The coefficient of static friction between the surfaces in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface?
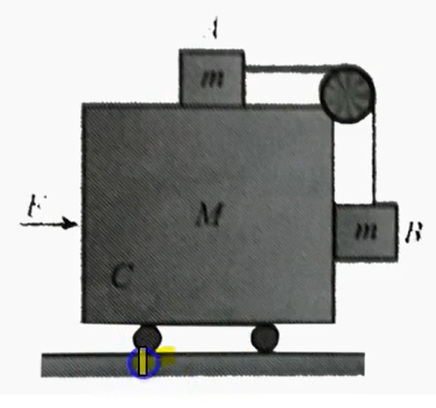
View SolutionConsider the situation shown in figure. The horizontal surface below the bigger block is smooth. The coefficient of friction between the blocks is μ. Find the minimum and the maximum force F that can be applied in order to keep the smaller block at rest with respect to the bigger block.
View SolutionA force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View SolutionFour block are arranged on a smooth horizontal surface as shown in figure .The masses of the blocks are given (see the fig ) The coefficient of static friction between the top and the bottom blocks is μs What is the maximum value of the horizontal force F applied to one of the bottom blocks as shown that makes all four block with the same acceleration ?

View Solution
