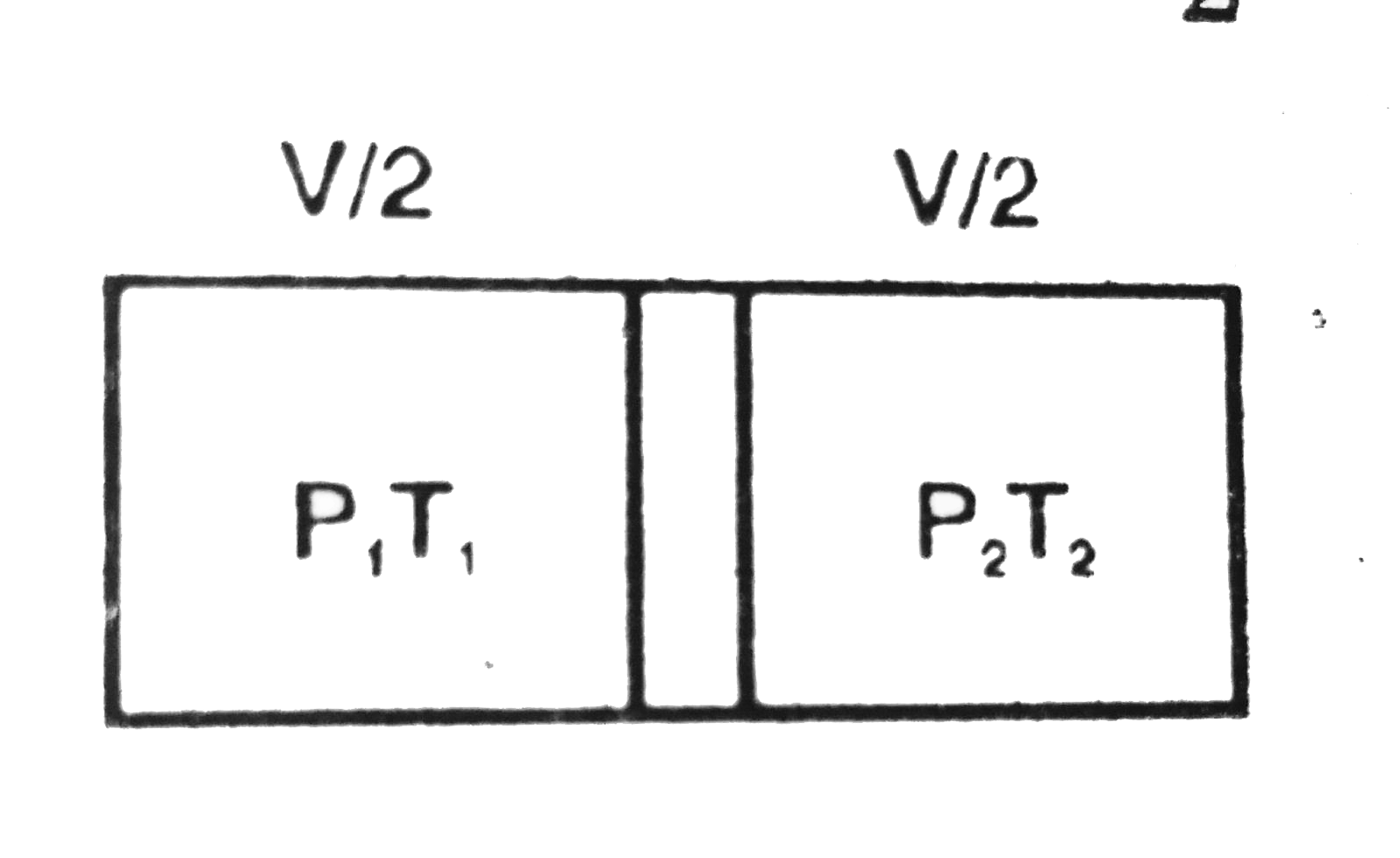
Figure shows an adiabatic cylindrical tube of volume (V0) divided in two parts by a frictionless adibatic separator . Initially, the separator is kept in the middle, an ideal gas at pressure (p1) and the temperatures (T1) is injected into the left part and the another ideal gas at pressures (P2) and temperature (T2) is injected into the right part. (CpCv=γ) is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the volumes of the parts, (b) the heat given to the gas in the left part and (c) the final common pressure of the gases.

For an adiabatic process, PVγ=Constant
So P1Vγ1=P2Vγ2 … (i)
According to the problem
V1+V2=V0
Then the euation (i)
P1Vγ2=P2(V0−V1)γ
or (P1P2)1γ=V0−V1V1
or V1−P1γ1=V0−P1γ2−V1P1γ2
or V1(P1γ1+P1γ2)=V0P1γ2
or V1=P1γ2V0P1γ1+P1γ2
V2=P1γ1V0P1γ1+P1γ2
(b) Since the whole process takes place in adiabatic surroundings, the separator is adiabatic.
Hence heat given to the gas in the left part = 0
(c) There will be a common pressure 'p' when the equilibrium is reached.
P1Vγ1+P2Vγ2=PVγ0
For equilibrium, V1=V2=V02
Hence,
P1(V02)γ+P2(V02)γ=P(V0)γ
P=⎛⎜
⎜⎝P1γ1+P1γ22⎞⎟
⎟⎠γ 
Topper's Solved these Questions
Similar Questions
In given figure, an adiabatic cylindrical tube of volume 2V0 is divided in two equal parts by a frictionless adiabatic separator. An ideal gas in left side of a tube having pressure P1 and temperature T1 where as in the right side having pressure P2 and temperature T2.Cp/Cv=γ is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the final volumes of the two parts (b) the heat given to the gas in the left part and (c) the final common pressure of the gases,
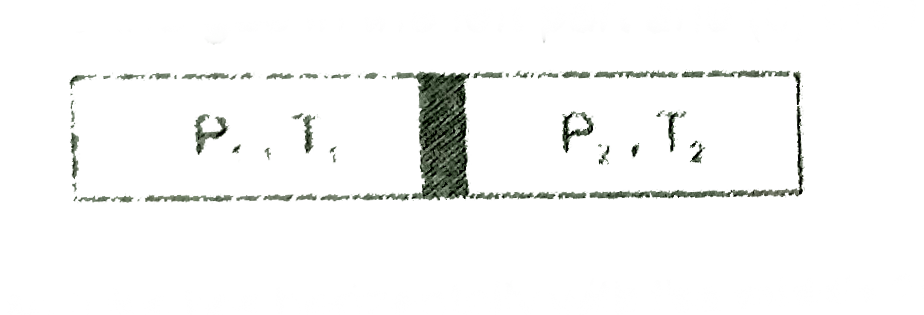
View SolutionAn ideal gas has pressure P, volume V and temperature T. Select the correct option.
View Solution
Knowledge Check
Following figure shows on adiabatic cylindrical container of volume V0 divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas (Cp/Cy=λ) is at pressure P and temperature T in left part and gas at pressure P and temperature T in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (Suppose x = displacement of the piston)
 AP2BP1CP1(V02)λ(V02+Ax)λDP2(V02)λ(V02+Ax)λ
AP2BP1CP1(V02)λ(V02+Ax)λDP2(V02)λ(V02+Ax)λAn insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1. The other chambers has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partion is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
AT1T2(P1V1+P2V2)P1V1T2+P2V2T1BP1V1T1+P2V2T2P1V1+P2V2CP1V1T2+P2V2T1P1V1+P2V2DT1T2(P1V1+P2V2)P1V1T1+P2V2T2The pressure P, Volume V and temperature T of a gas in the jar A and the other gas in the jar B at pressure 2P, volume V/4 and temperature 2T, then the ratio of the number of molecules in the jar A and B will be
A1:1B1:2C2:1D4:1
Show a cylindrical tube of volume V_(0) divided in two parts by a frictionless separator. The walls of the tube are adiabatic but the separator is conducting, Ideal gases ate filled in the two parts. When the swparator is kept in the middle, the pressure are p_(1) and p-(2) in the left part and the right part respectively. The separator is slowly slid and is released at a position where it can stay in equilibrium. Find the volumes if the two parts. (figure)
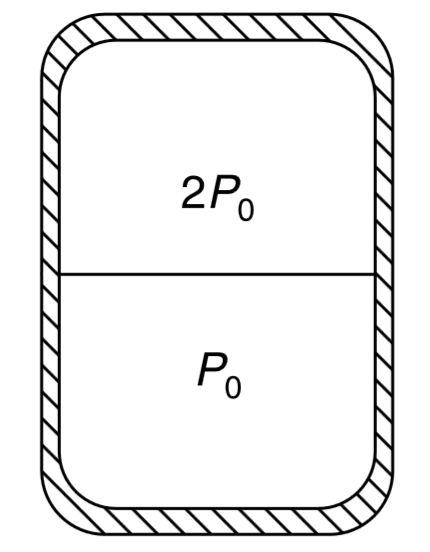
View SolutionA cylindrical container of volume V0 is divided into two parts by a thin conducting separator of negligible mass. The walls of the container are adiabatic. Ideal gases are filled in the two parts such that the pressures are P0 and 2P0 when the separator is held in the middle of the container (see figure). Now the separator is slowly slid and released in a position where it stays in equilibrium. Find the volume of the two parts.
View SolutionAn adiabatic vessel of total volume V is divided into two equal parts by a conducting separtor. The is fixed in this position. The part on the left contains one mole of an ideal gas (U=1.5nRT) and the part on the right contains two moles of the same gas. initially, the pressure on each side is p. the system is left for sufficiant time so that a steady state is reached. find (a) the work done by the gas in the left part during the process, (b) the temperature on the two sides in the beginning, (c ) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
View SolutionThe pressure P, volume V and temperature T of a gas in the jqar A and other gas in the jar B as at pressure 2P, volume V/4 and temperature 2T, then the ratio of the number of molecules in the jar A and B will be
View SolutionAn insulated container of gas has two chambers separated by an insulating partition. One of the chmabers has volume V1 and contains ideal gas at pressure P1 and temperature T1.The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
View Solution
