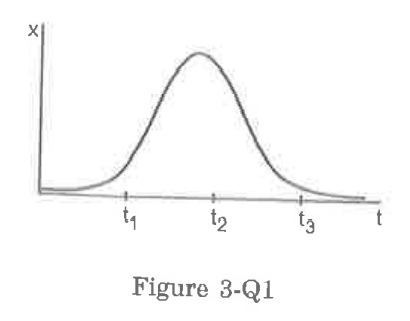
Figure shows the x coordinate of a particle as a function of time. Find the signs of vxandax at t=t1,t=t2andt=t3.
 Solution in Tamil
Solution in Tamil
Step by step video & image solution for Figure shows the x coordinate of a particle as a function of time. Find the signs of v_x and a_x at t=t_1,t=t_2 and t=t_3. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -1
13 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -2
10 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - worked out Examples
20 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
Similar Questions
A motor car is going due north at a speed of 50 km/h. It makes a 900 left turn without changing the speed. The change in the velocity of the car is about
View SolutionConsider the motion of the tip of the minute hand of a clock. In one hour
View SolutionA man at a speed of 6 km/hr for 1 km and 8 km/hr for the next 1 km. What is t his average speed for the walk of 2 km?
View SolutionA vector →A makes an angle of 20∘and→B makes an angle of 110∘ with the X-axis. The magnitude of these vectors are 3 m and 4 m respectively.Find the resultant
View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration.
View SolutionThe vertices of a triangle are [a t_1t_2,a(t_1 +t_2)], [a t_2t_3,a(t_2 +t_3)], [a t_3t_1,a(t_3 +t_1)] Then the orthocenter of the triangle is (a) (-a, a(t_1+t_2+t_3)-at_1t_2t_3) (b) (-a, a(t_1+t_2+t_3)+at_1t_2t_3) (c) (a, a(t_1+t_2+t_3)+at_1t_2t_3) (d) (a, a(t_1+t_2+t_3)-at_1t_2t_3)
View SolutionFigure shows the displacement-time graph of a particle moving in a straight line. Find the signs of velocity and acceleration of particle at time t = t_1 and t = t_2.
View SolutionFigure shows (v_x ,t) and (v_y ,t) diagram for a body of unit mass. Find the force as a function of time.
View SolutionLet T be the set of all triangles in a plane with R a relation in T given by R={(T1,T2):T1 is congruent to T2}. Show that R is an equivalence relation.
View SolutionLet T be the set of all triangles in a plane with R a relation in T given by R={(T1,T2):T1≅T2}. Show that R is an equivalence relation.
View SolutionFigure shows (v_x ,t) and (v_y ,t) diagram for a body of unit mass. Find the force as a function of time.
View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+at1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is: (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+a(t1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
View SolutionLet T be the set of all triangles in a plane with R a relation in T given by : R={(T1,T2):T1 is congruent to T_2}. Show that R is an equivalence relation.
View SolutionThe displacement x of a particle with a function of time t is shown in the figure. The graph shows that
View SolutionFigure shows the displacement-time graph of a particle moving in a straight line. Find the signs of velocity and acceleration of particle at time t=t1andt=t2.

View Solution
