Question

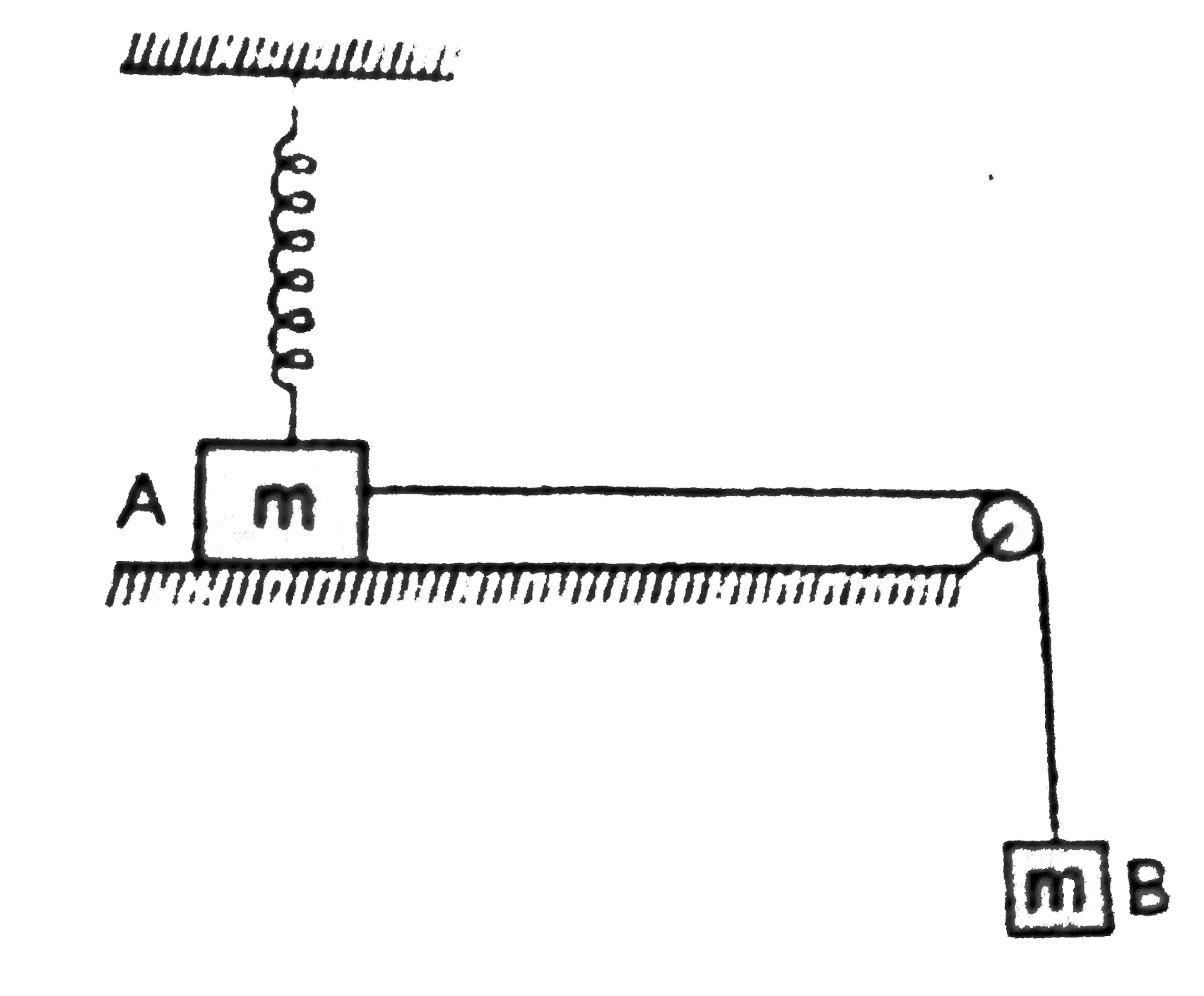
Figure shows two block $A$ and $B$, each having a mass of 320 g connected by a light string passing over a smooth light pulley. The horizontal surface on which the block $A$ can slide is smooth. The block $A$ is attached to spring constant $40N/m$ whose other end is fixed to a support 40 cm above the horizontal surface. Initially, the spring is vertical and unstretched when the system is released to move. Find the velocity of the block A at the instant it breaks off the surface below it. Take $g=10m/s^2$ .

Answer

A

Explanation

`m=320g=0.32 kg, k=40 N/m`
`h=40cm=0.4m,g=10m/sec^2`
From the free body diagram,
`kxcostheta=mg`
(when the block breaks of R=0)`
`rarr costheta=(mg)/(kx)`
`rarr 0.4/(0.4+x=3.2/(40x)`
`rarr 16x=3.2x+1.28`
`rarr x=0.1m`
So, `s=AB=sqrt((h+x^2)-h^2)`
`=sqrt((0.5)^2-(0.4)^2)`=0.3m`
Let the velocity of tebody at B be v change in K.E. work done (for the system)
`(1/2mu^2+1/2mv^2)=-1/2kx^2+mgs`
`rarr (0.32)xxv^2`
`=-(1/2)xx40xx(1.0)^2+(0.2)xx10xx(0.3)`
`rarr v=1.5m/sec`
`From the ure
`/_\l=h(sectheta-1)`........i
From the energy conservation
`mgs=2[1/2mv^2]+1/2K/_\l^2`
` mgh than theta =mv^2+1/2kh^2(sectheta-1)^2`.....ii
From the law of motion at break of
`mgkh(sectheta-1)costheta`
`rarr 1-costheta=mg/kh`
`rarr costheta=1-mg/kh`
`or costheta=(kh-mg)/kh`
or `costheta=(kh-mg)/kh`
`=(40xx0.4-0.32xx10)/(40xx0.4)`
`=0.8`
Putting the value of `theta` in equation i,
`0.32xx10xx0.4xx0.75`
`=0.32v^2+1/240xx(0.4)^2(1.25-1)^2`
`rarr 0.96=0.32v^2+0.2`
`rarr `0.32v^2=0.72`
`rarr v=1.5m/sec