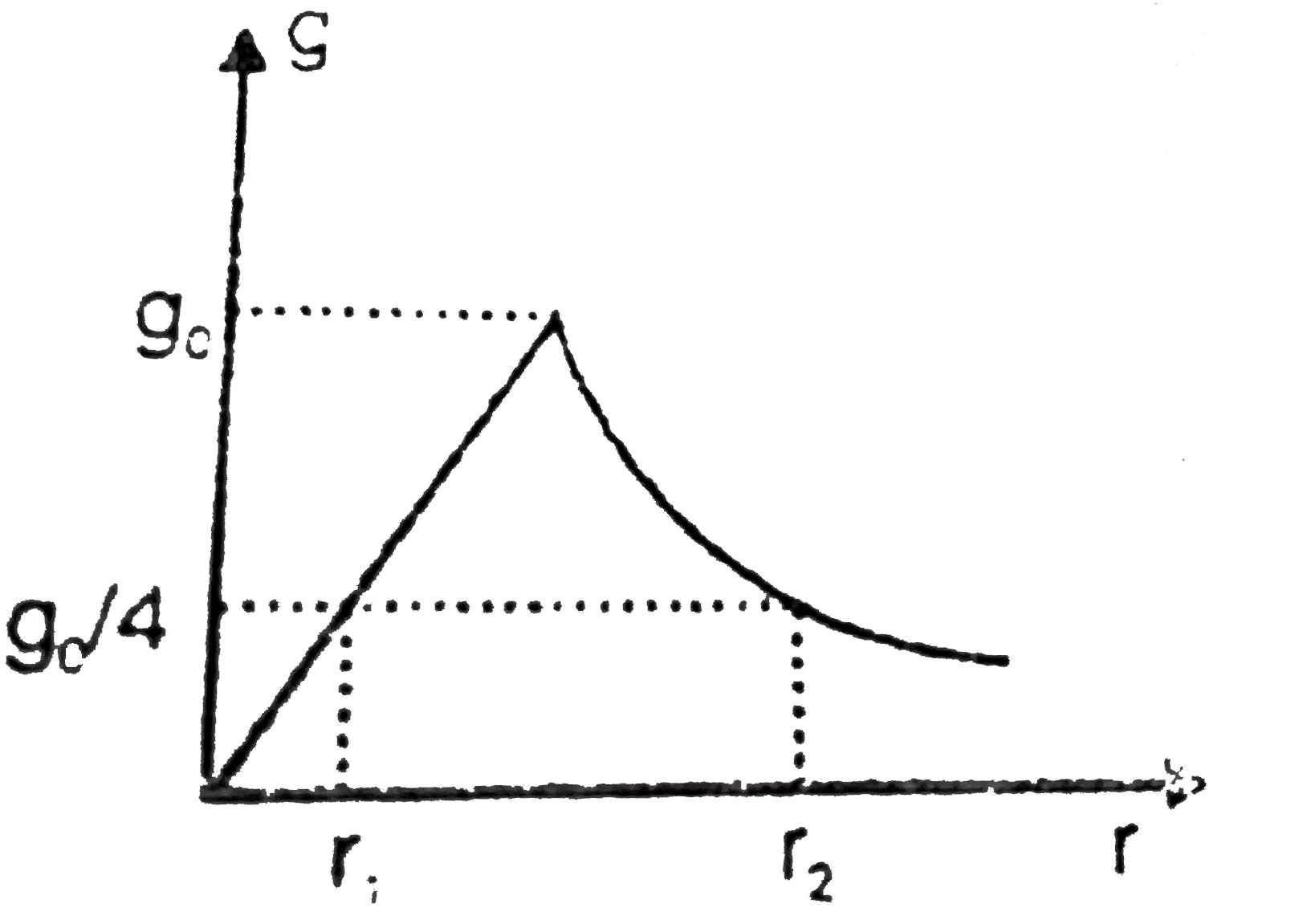
Figure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r2−r1
A

B

C

D

Video Solution
Text Solution
The correct Answer is:D
Inside the earth

r<Re,g.=g(1−dRe)=g(Re−dRe)
g.=gRer

For r=Re,g.=g
For r>Re,g.=GMr2

|
Topper's Solved these Questions
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - COMPETITION FILE ( Jee (Advanced) for IIT Entrance)
6 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - COMPETITION FILE ( C. Multiple Choice Questions)
12 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - COMPETITION FILE (B.(Multipe Choice Questions from Competitive Examinations) AIPMT/NEET & Other State Boards for Medical Entrance)
16 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
Similar Questions
Knowledge Check
Figure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
 AR4B7R4C4R3D2R
AR4B7R4C4R3D2RVariation of acceleration due to gravity (g) with distance x from the centre of the Earth is best represented by (R→ Radius of the Earth)
A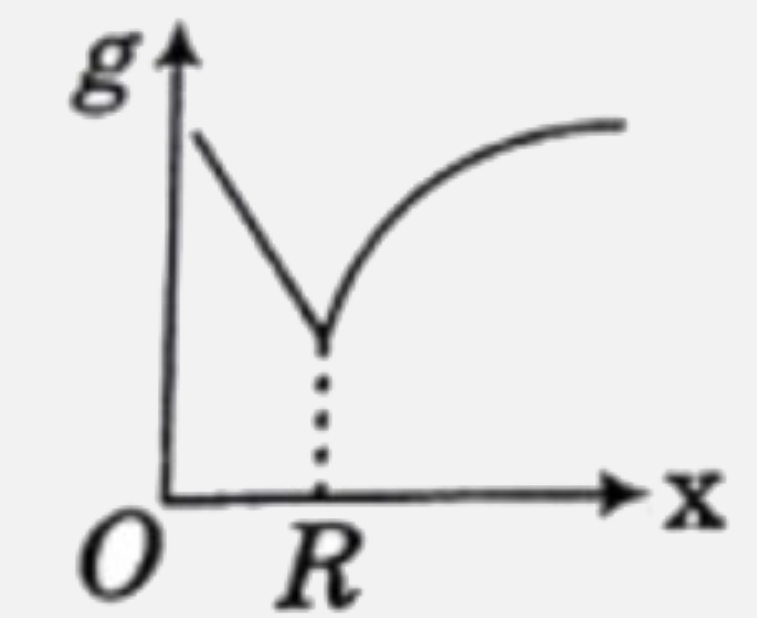 B
B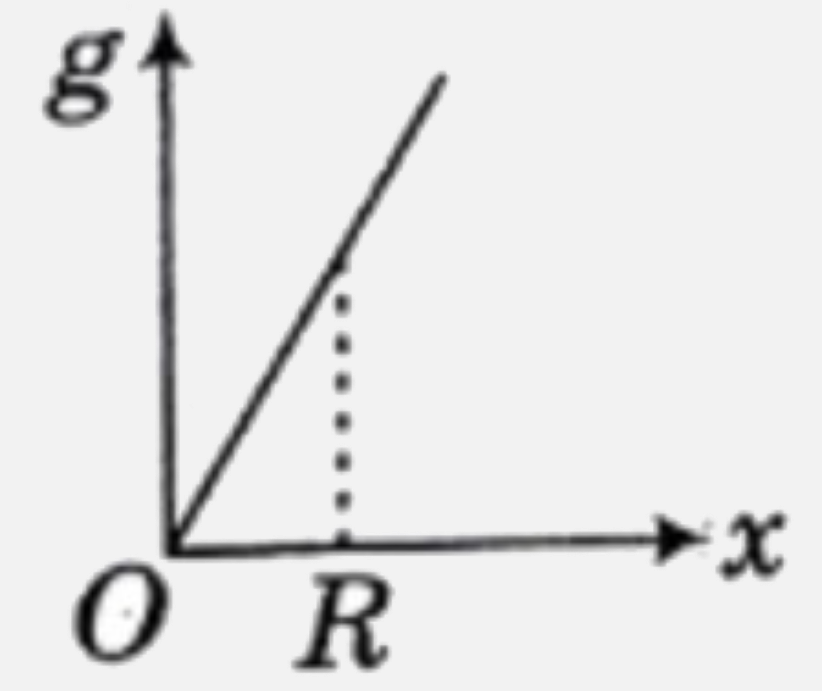 C
C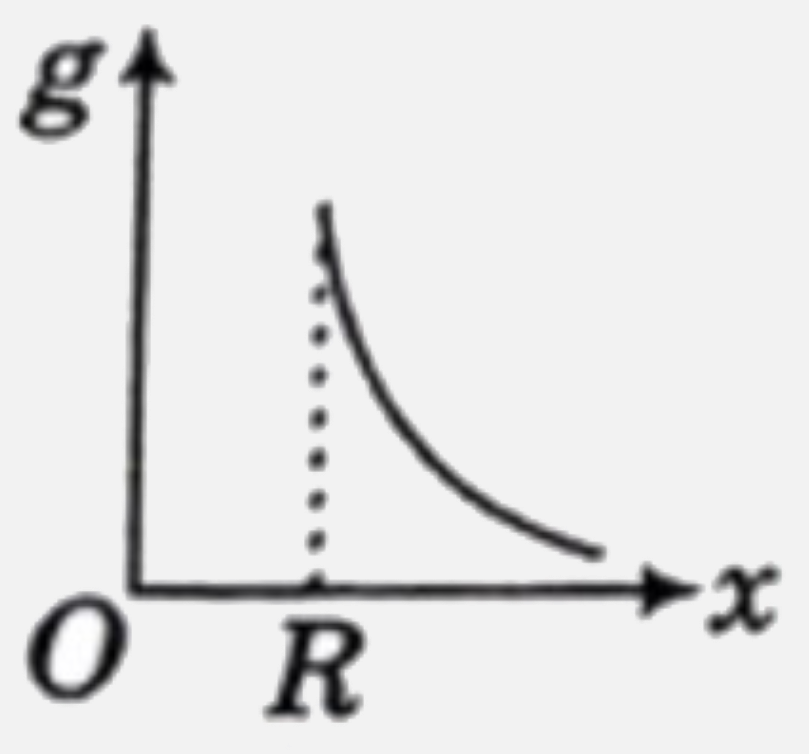 D
D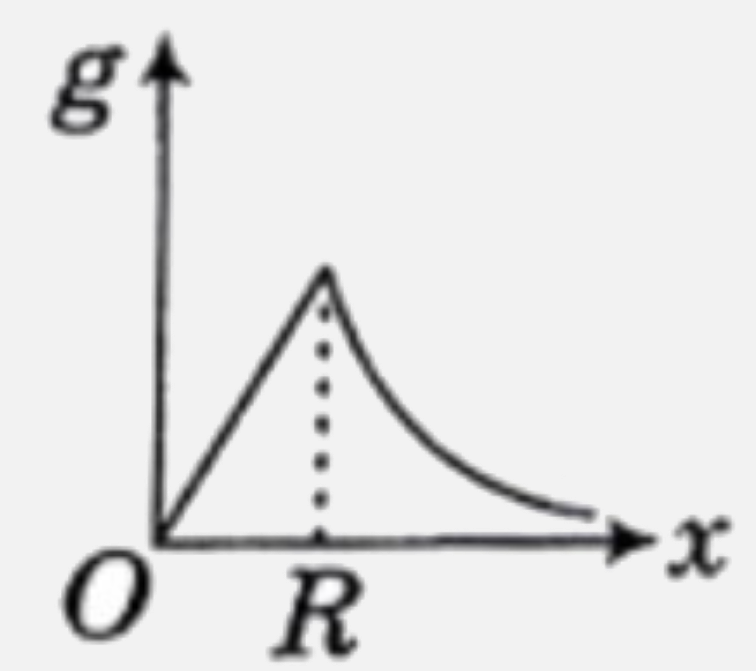
The acceleration due to gravity is g at a point distant r from the centre of earth of radius R. If r<R, then
Ag∝rBg∝r2Cg∝r−1Dg∝r−2
If g denotes the value of acceleration due to gravity at a point distance r from the centre of earth of radius R. If r<R, then
View SolutionA particle at a distance r from the centre of a uniform spherical planet of mass M radius R (ltr) has a velocity of magnitude v.
View SolutionThe acceleration due to gravity near the surface of a planet of radius R and density d is proportional to
View SolutionThe acceleration due to gravity near the surface of a planet of radius R and density d is proportional to
View SolutionThe acceleration due to gravity near the surface of a planet of radius R and density d is proportional to
View Solution
