A particle at a distance r from the centre of a uniform spherical planet of mass M radius R (ltr) has a velocity of magnitude v.
for 0<v<√GMr trajectory may be ellipse
for v =√GMr trajectory may be ellipse
for √GMr<v<√2GMr trajectory may be ellipse.
for v =sqrt((GM)/r trajectory may be circle
The correct Answer is:A, B, C, D
Orbital speed (v0)=√GMR
escapes speed (ve)=√2GMR
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Subjective
107 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Match the column :
A particle at a distance r from the centre of a uniform spherical planet of mass M radius R(<r) has a velocity v magnitude of which is given in column I. Match trajectory from column II about possible nature of orbit.
Column IColumn II(A)0<V<√GMr(P)Straight line(B)√GMr(Q)Circle(C)√2GMr(R)Parabola(D)v>√2GMr(S)Ellipse
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View Solution
Knowledge Check
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMRP is a point at a distance r from the centre of a spherical shell of mass M and radius a, where r<a. The gravitational potential at P is
A−GMrB−GMaC−GMra2D−GM(a−ra2)A particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
A−GmRB−3GmRC−4GmRD−2GmR
A particle of mass M is placed at the centre of a spherical shell of same mass and radius a. What will be the magnitude of the gravitational potential at a point situated at a/2 distance from the centre ?
View SolutionThe distance of the centre of mass of a hemispherical shell of radius R from its centre is
View SolutionA point mass m0 is placed at distance R/3 from the centre of spherical shell of mass m and radius R. the gravitational force on the point mass m0 is
View SolutionA particle of mass m is ocated at a distance r from the centre of shell of mass M and radius R. The force between the shell and mass F(r). The plot of F(r) ve r is :
View SolutionFigure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
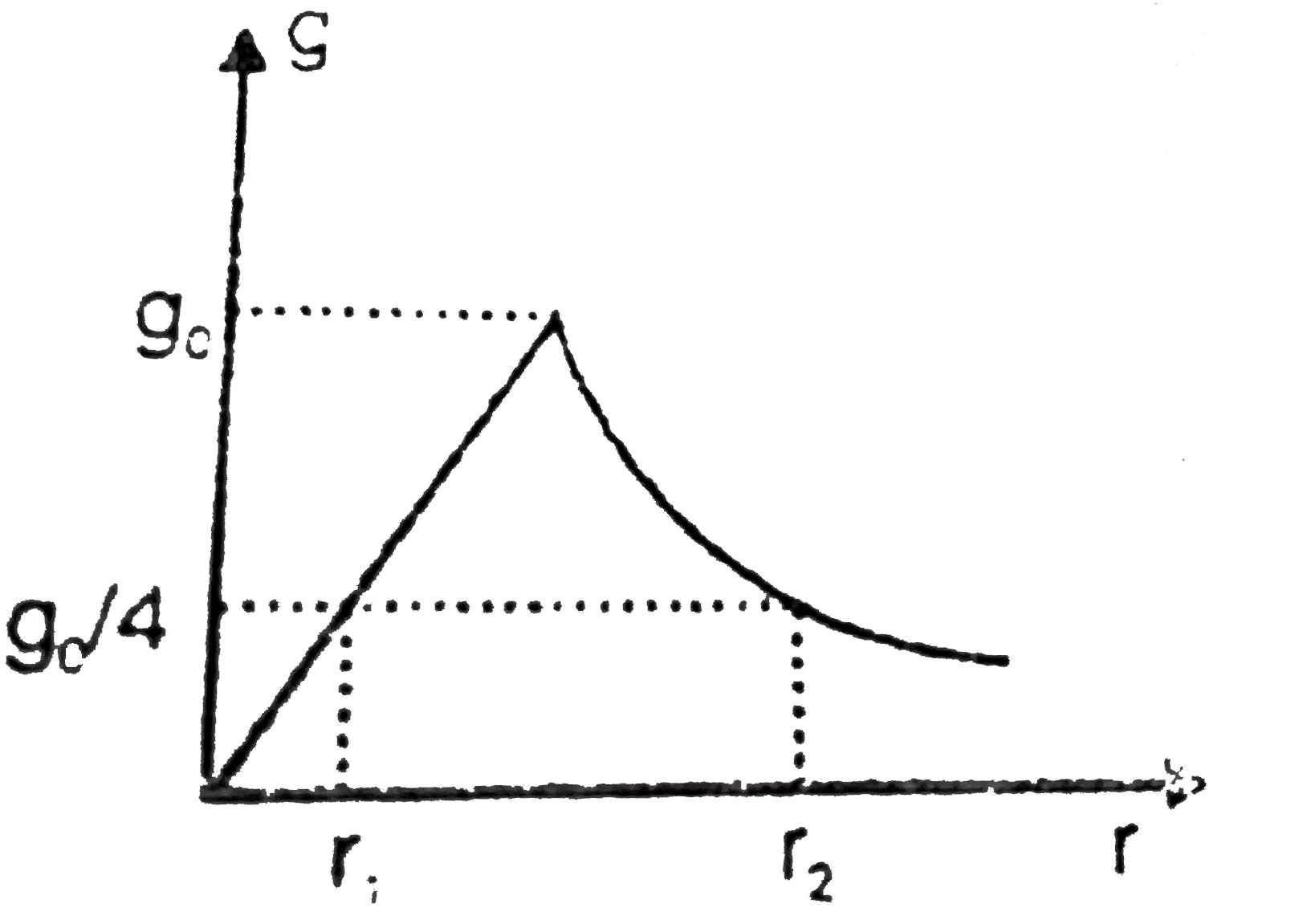
View Solution
