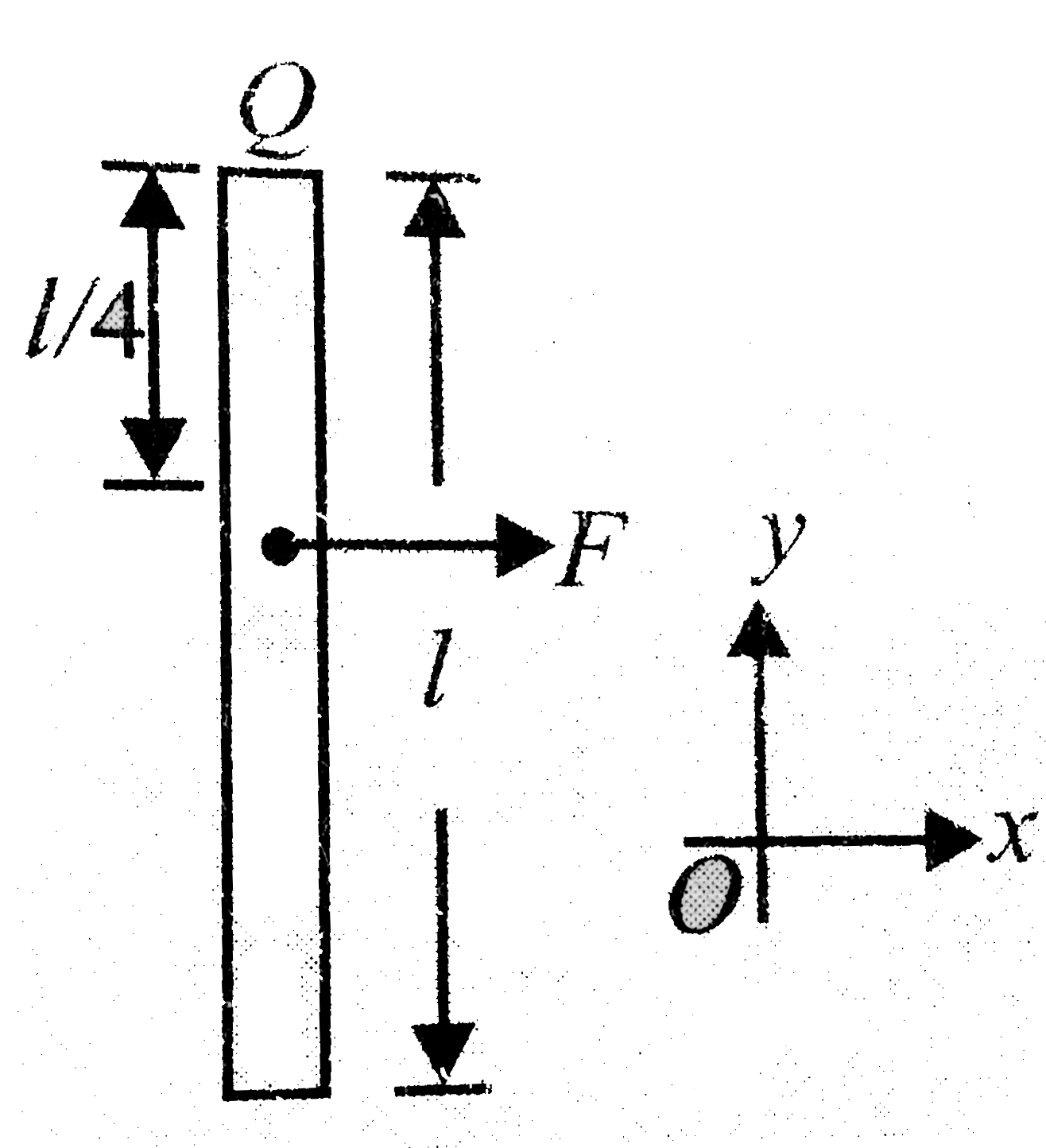
 Find α,aQ and the point of zero acceleration when the horizontal force F acts on the smooth rod of mass m and length l which is kept on a horizontal surface.
Find α,aQ and the point of zero acceleration when the horizontal force F acts on the smooth rod of mass m and length l which is kept on a horizontal surface.
τcm=Icmα
Fl4=Iml212α⇒α=3Fml
acm=Fm
aQ=acm+αl2=Fm+3Fmll2=5F2m
Let acceleration of a point P (which is distance x between centre of mass) is zero then
ap=acm−αx=0
⇒Fm−3Fmlx=0⇒x=l3
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Single Correct
97 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.3
15 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Find aC and α of the smooth rod of mass m and length l.
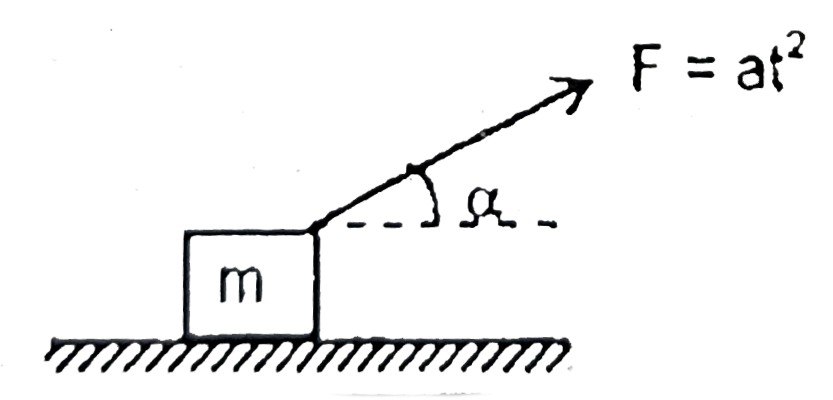
View SolutionAt t=0, a force F=at2 is applied to a small body of mass m at an angle α resting on a smooth horizontal plane
View Solution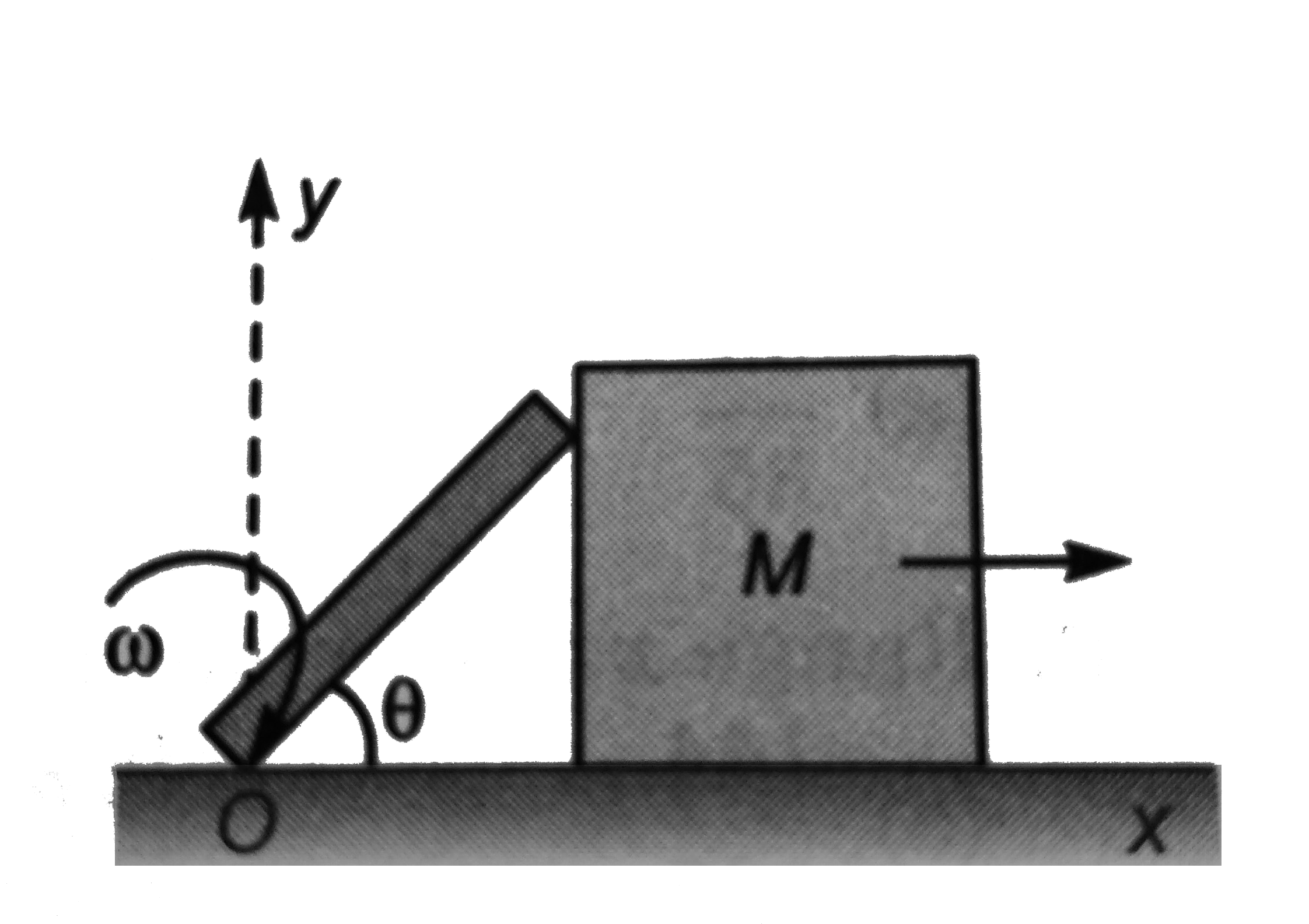
A uniform rod of mass m and length l is applied pivoted at point O. The rod is initially in vertical position and touching a block of mass M which is at rest on a horizontal surface. The rod is given a slight jerk and it starts rotating about point O this causes the block to move forward as shown The rod loses contact with the block at θ=30∘ all surfaces are smooth now answer the following questions.
Q. The acceleration of centre of mass of rod, when it loses contact with the block is
View Solution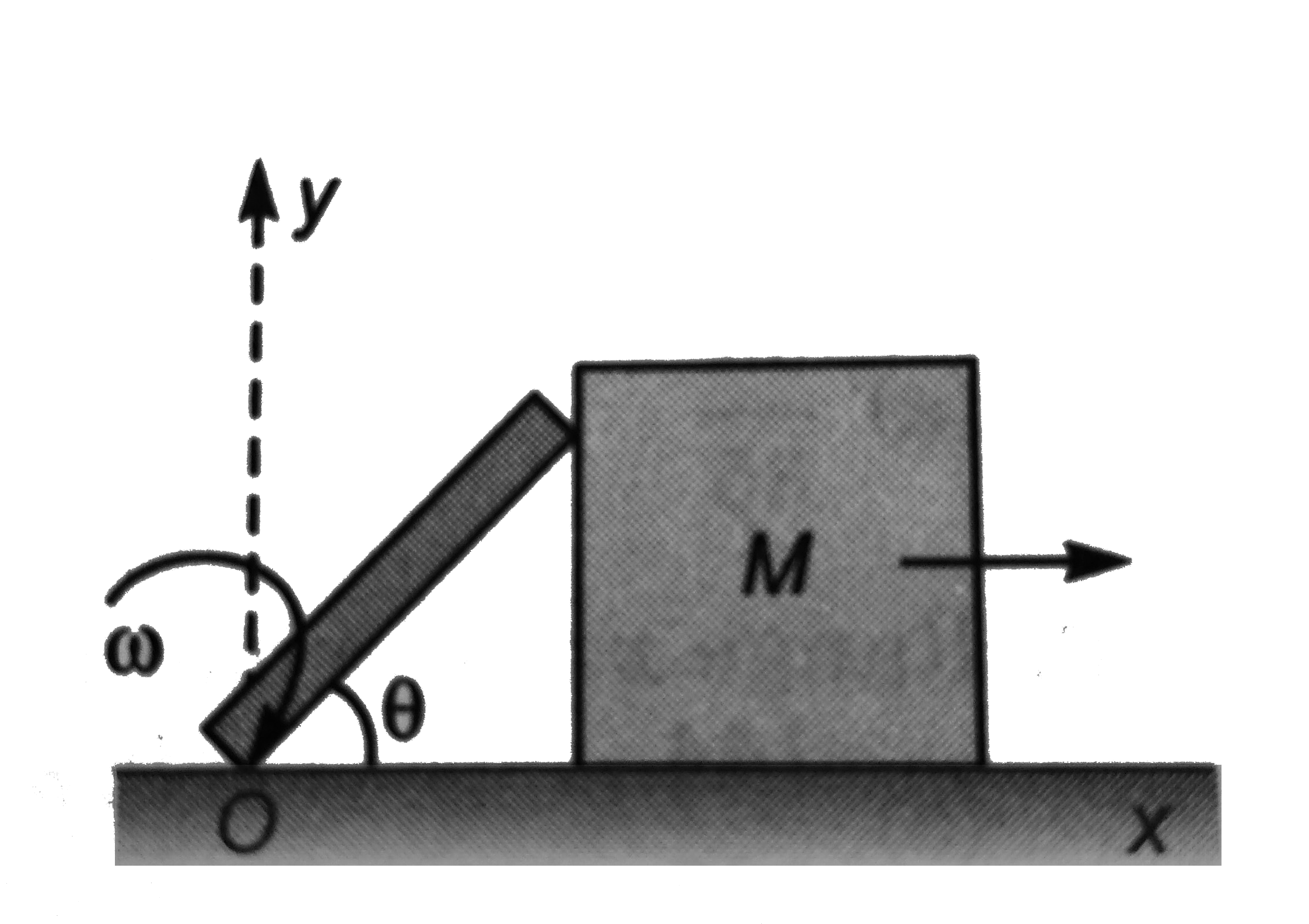
A uniform rod of mass m and length l is applied pivoted at point O. The rod is initially in vertical position and touching a block of mass M which is at rest on a horizontal surface. The rod is given a slight jerk and it starts rotating about point O this causes the block to move forward as shown The rod loses contact with the block at θ=30∘ all surfaces are smooth now answer the following questions.
Q. The velocity of block when the rod loses contact with the block is
View Solution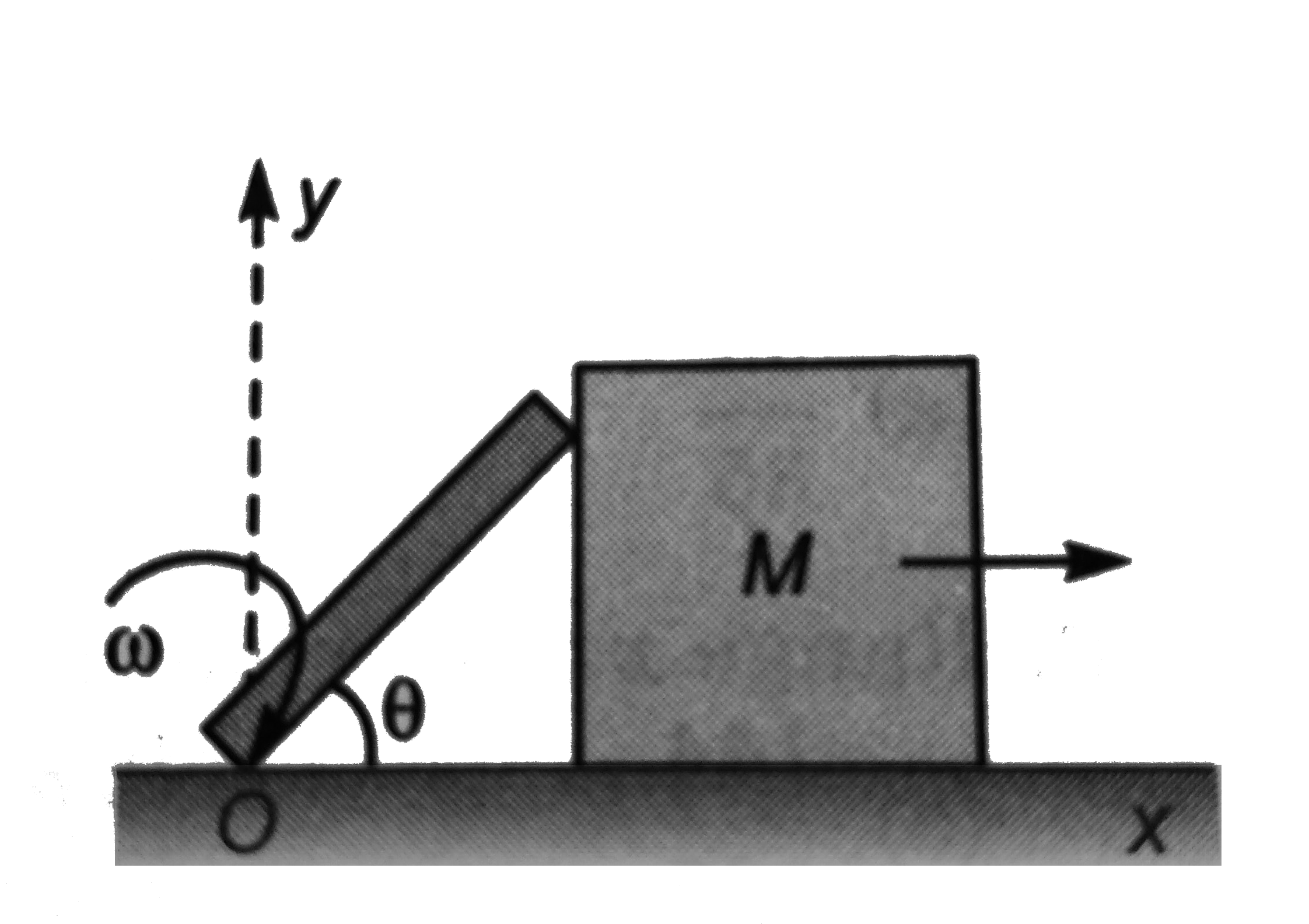
A uniform rod of mass m and length l is applied pivoted at point O. The rod is initially in vertical position and touching a block of mass M which is at rest on a horizontal surface. The rod is given a slight jerk and it starts rotating about point O this causes the block to move forward as shown The rod loses contact with the block at θ=30∘ all surfaces are smooth now answer the following questions.
Q. The hinge reaction at O on the rod when it loses contact with the block is
View SolutionA block of mass M is being pulled with the help of a string of mass m and length L. the horizontal force applied by the man on the string is F.

Determine
(a) Find the force exerted by the string on the block and acceleration of system.
(b) Find the tension at the mid point of the string.
(c ) Find the tension at a distance x from the end at which force is applied.
Assume that the block is kept on a frictionless horizontal surface and the mass is uniformly distributed in the string.
View SolutionA force P acts on a smooth block of mass m placed on a horizontal floor at an angle θ with with horizontal on the block
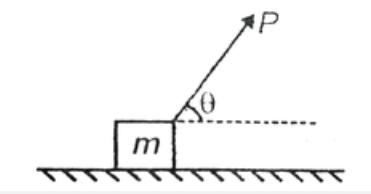
View SolutionA rod of mass M and length L is placed on a smooth horizontal surface. It is hinged at one end so that it can rotate freely in a horizontal circle about this end. There exists a uniform magnetic field →B perpendicular, into the horizontal surface everywhere. The strength of magnetic field starts varying as B=B0t.
(i) Find the torque acting on the rod about its hinged end.
(ii) Find the reaction produced at hinge at t = 0.
(A charge Q is distributed uniformaly on the rod)
View SolutionA body of mass 10 kg lies on a rough horizontal surface. When a horizontal force of F newtons acts on it, it gets an acceleration of 5m/s2. And when the horizontal force is doubled, it gets an acceleration of 18m/s2. The coefficient of friction between the body and the horizontal surface is
View SolutionA uniform rod of mass M and length L is standing vertically along the y-axis on a smooth horizontal surface as shown. A small disturbance causes the lower end to slip on the smooth horizontal surface and rod starts falling. The path followed by centre of mass of the rod during the fall is

View Solution
