A uniform solid. cylinder $A$ of mass can freely rotate about a horizontal axis fixed to a mount of mass $m_{2}$ . A constant horizontal force $F$ is applied to the end $K$ of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find the acceleration of the point $K$ .

Video Solution

Text Solution

Verified by Experts

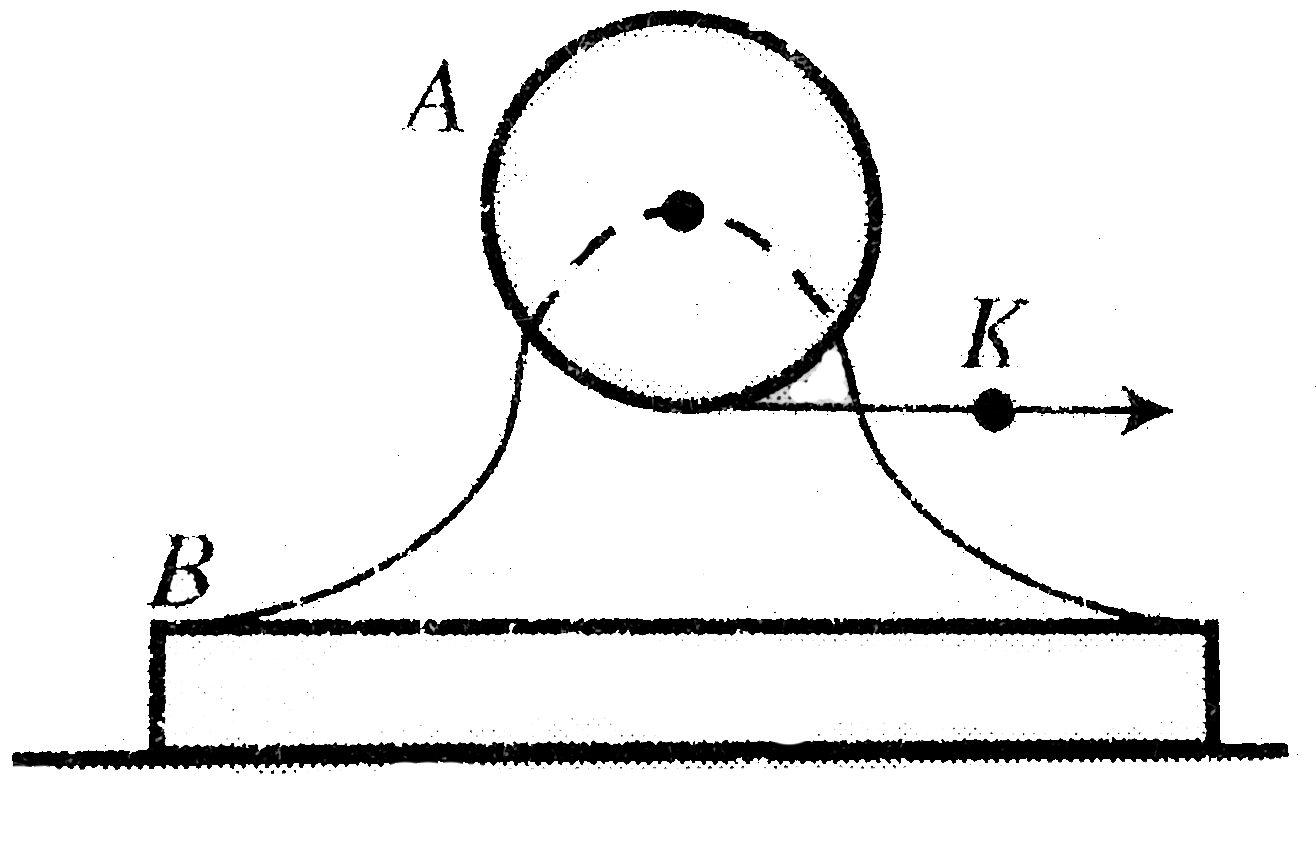
The acceleration whole system $a_{1} = \frac{F}{m_{1} + m_{2}}$
The acceleration of the point $K$ w.r.t the axis of the cylinder $a_{2} = α R$
where $α$ is given by
$F R = I α$ or $α = \frac{F R}{m_{1} R^{2} / 2} = \frac{2 F}{m_{1} R}$
$\Rightarrow a_{2} = \frac{2 F}{m_{1}}$
The acceleration of the point $K$ w.r.t ground
$= a_{1} + a_{2} = \frac{F}{m_{1} + m_{2}} + \frac{2 F}{m_{1}} = F \frac{(3 m_{1} + 2 m_{2})}{m_{1} (m_{1} + m_{2})}$

Updated on:21/07/2023

|

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 1-Exercise 2.4

Home
Ask Doubt
Profile