Find force F required to keep the system in equilibrium. The dimensions of the system are d=0.3m and a=0.2m. Assume the rods to be massless.

150(ˆi)
150(−ˆk)
150(−ˆi)
it cannot be in equilibrium
The correct Answer is:C
Net torque about C is zero
Fa+100x=0
F=−100da=−150
→F=−150ˆi
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
For a system in equilibrium, ΔG=0, under conditions of constant
View SolutionIf system is in equilibrium then find relation between m1 and m2
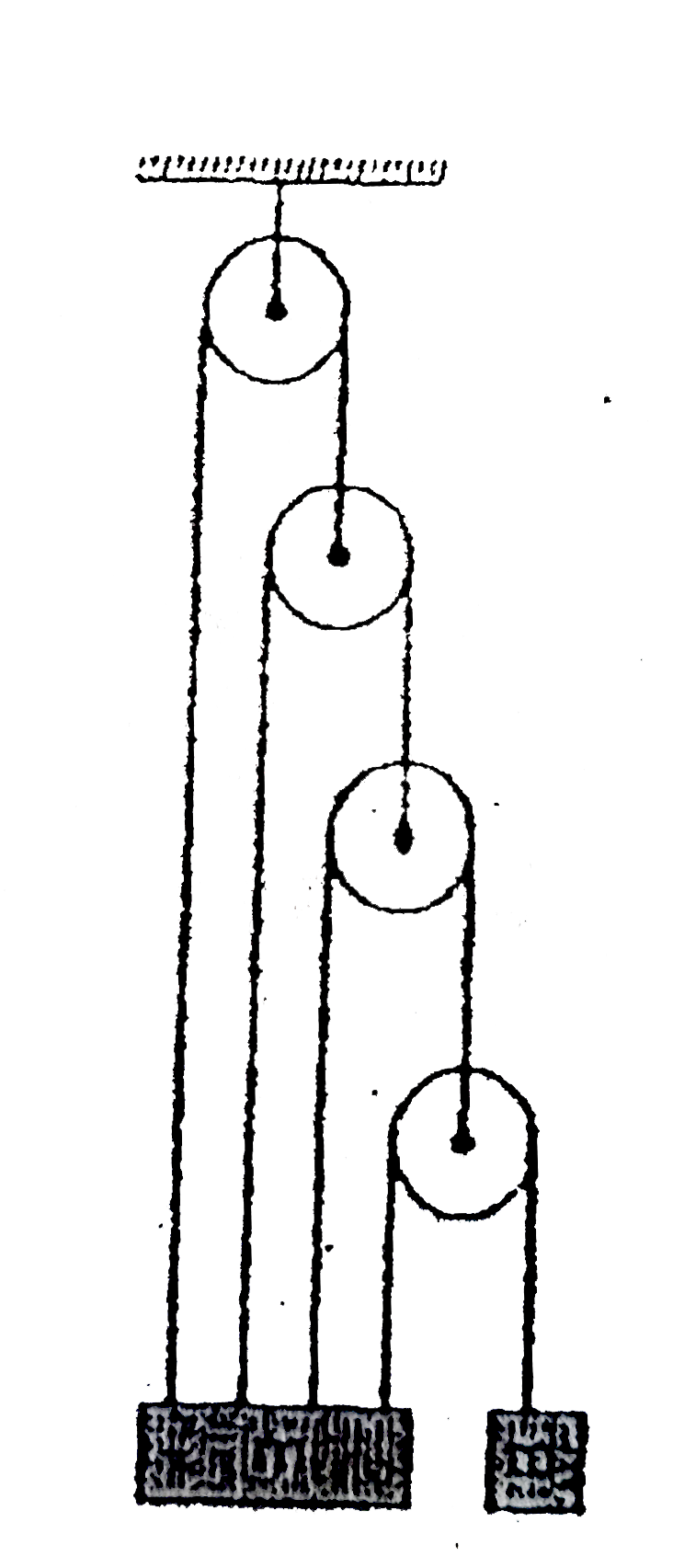
View SolutionFind m3 if the system is in equilibrium the incline is smooth and string and pulley are light
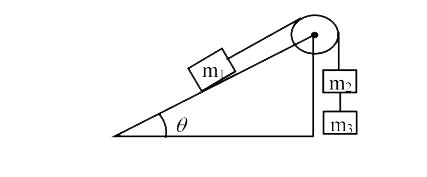
View SolutionFor equilibrium of the system, value of mass m should be

View SolutionFor the equilibrium of the system shown, the value of mass m should be

View SolutionFor the system shown in figure , to be in equilibrium , determine mass m .

View SolutionA mass of 0.5 kg is hung from a spring. A gradually increasing 0.5 N force is required to pull the mass downward a distance of 0.25 m from its equilibrium position,if the mass is then released from this position, find
(a) The total energy of the system .
(b) The frequency of the oscillation
(c ) The speed and acceleration of the mass as it passes the equilibrium position.
(d) The speed and acceleration of the mass when the diplacement from equilibrium is 0.25 m
(e) For the initial condition stated, write down the diplacement equation of motion for this mass.
View SolutionFind the minimum force required to keep a block of mass m in equilibrium on a rough inclined plane with inclination α and coefficient of friction μ(<tanα).
View Solution
In the figure, at the free end of the light string, a force F is supplied to keep the suspended mass of 18 kg at rest. Then the force exerted by the ceiling on the system (assume that the string segments are vertical and the pulleys are light and smooth) is:(g=10ms2)
View SolutionFind the value of tension in string 1 if the system equilibrium ? (g=10 m/s2)
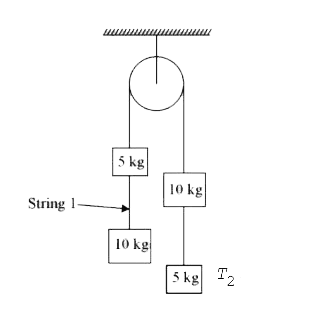
View Solution
