Question

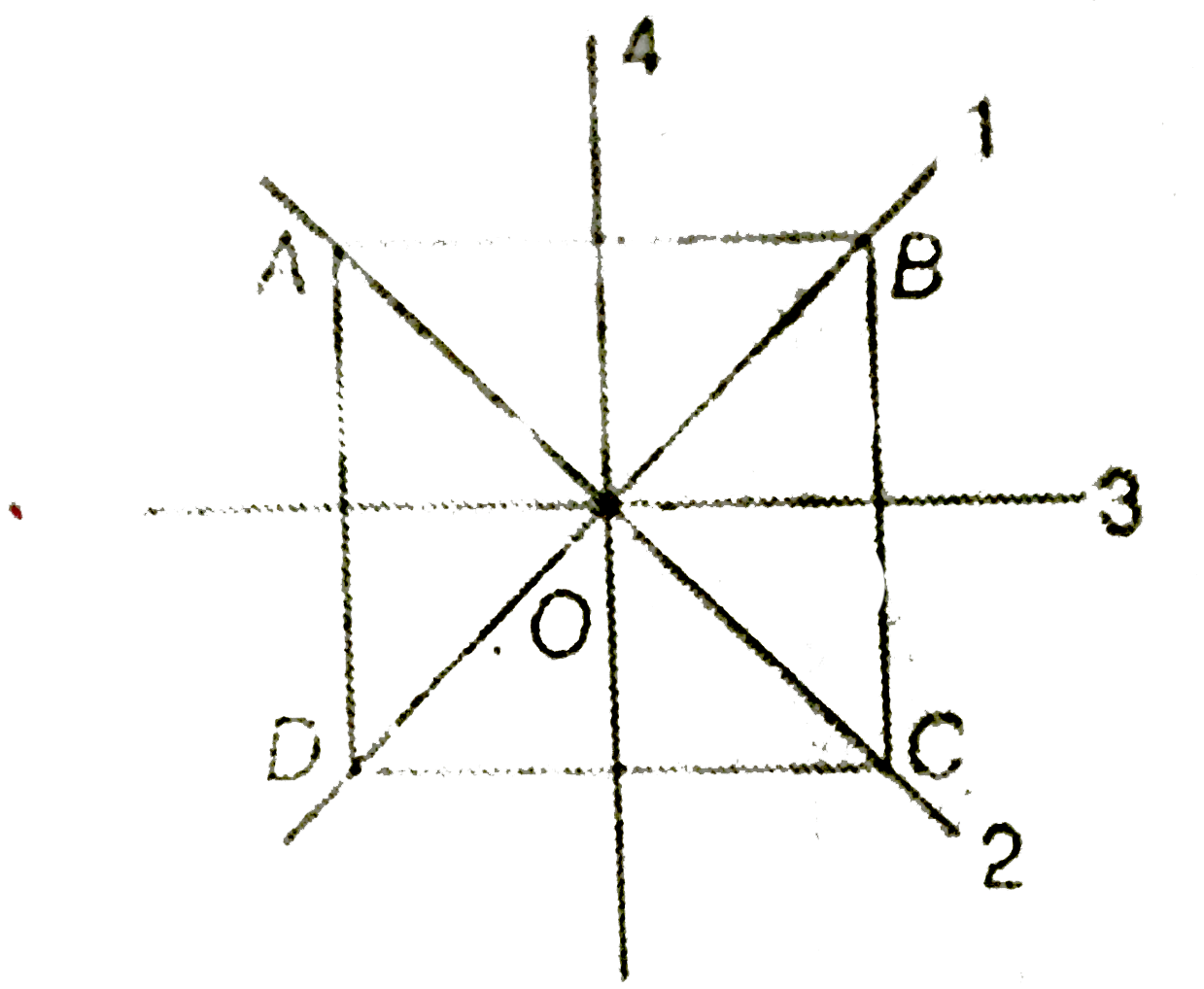
Let l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle $\theta$ with AB. The moment of inertia of the plate about the axis CD is then equal to

Options

A. `I`
B. `Isin^(2)theta`
C. `Icos^(2)theta`
D. `Icos^(2)(theta/2)`

Answer

A

Explanation

To find the moment of inertia of a uniform square plate about an axis CD that passes through its center and makes an angle θ with the axis AB, we can follow these steps:

1. Identify the Moment of Inertia about Axis AB:
- The moment of inertia \( I \) of a uniform square plate about an axis AB that passes through its center and is parallel to two of its sides is given as \( I \).

2. Use the Perpendicular Axis Theorem:
- According to the perpendicular axis theorem, for a planar object, the moment of inertia about an axis perpendicular to the plane (let's call it axis z) is the sum of the moments of inertia about two perpendicular axes in the plane (x and y).
- Therefore, we can write:
\( I_z = I_x + I_y \)
- Since the plate is uniform and symmetric, we have \( I_x = I_y = I \). Thus,
\( I_z = I + I = 2I \)

3. Consider the Moment of Inertia about Axis CD:
- Now, we need to find the moment of inertia about the axis CD, which makes an angle θ with the axis AB.
- Let’s denote the moment of inertia about the axis CD as \( I_0 \).

4. Analyze the Axes:
- The axis CD can be resolved into two components: one along AB and one perpendicular to AB.
- By symmetry, if we consider the axis perpendicular to CD (let's call it C'D'), the moment of inertia about C'D' will also be \( I_0 \).

5. Apply the Perpendicular Axis Theorem Again:
- For the axes CD and C'D', we can apply the perpendicular axis theorem:
\( I_z = I_0 + I_0 \)
- This implies:
\( I_z = 2I_0 \)

6. Relate the Moments of Inertia:
- From the previous step, we know that \( I_z = 2I \). Therefore, we can set the equations equal to each other:
\( 2I = 2I_0 \)
- Dividing both sides by 2 gives:
\( I = I_0 \)

7. Conclusion:
- Thus, the moment of inertia of the plate about the axis CD, which makes an angle θ with the axis AB, is:
\( I_0 = I \)

Final Answer:
The moment of inertia of the plate about the axis CD is equal to \( I \).