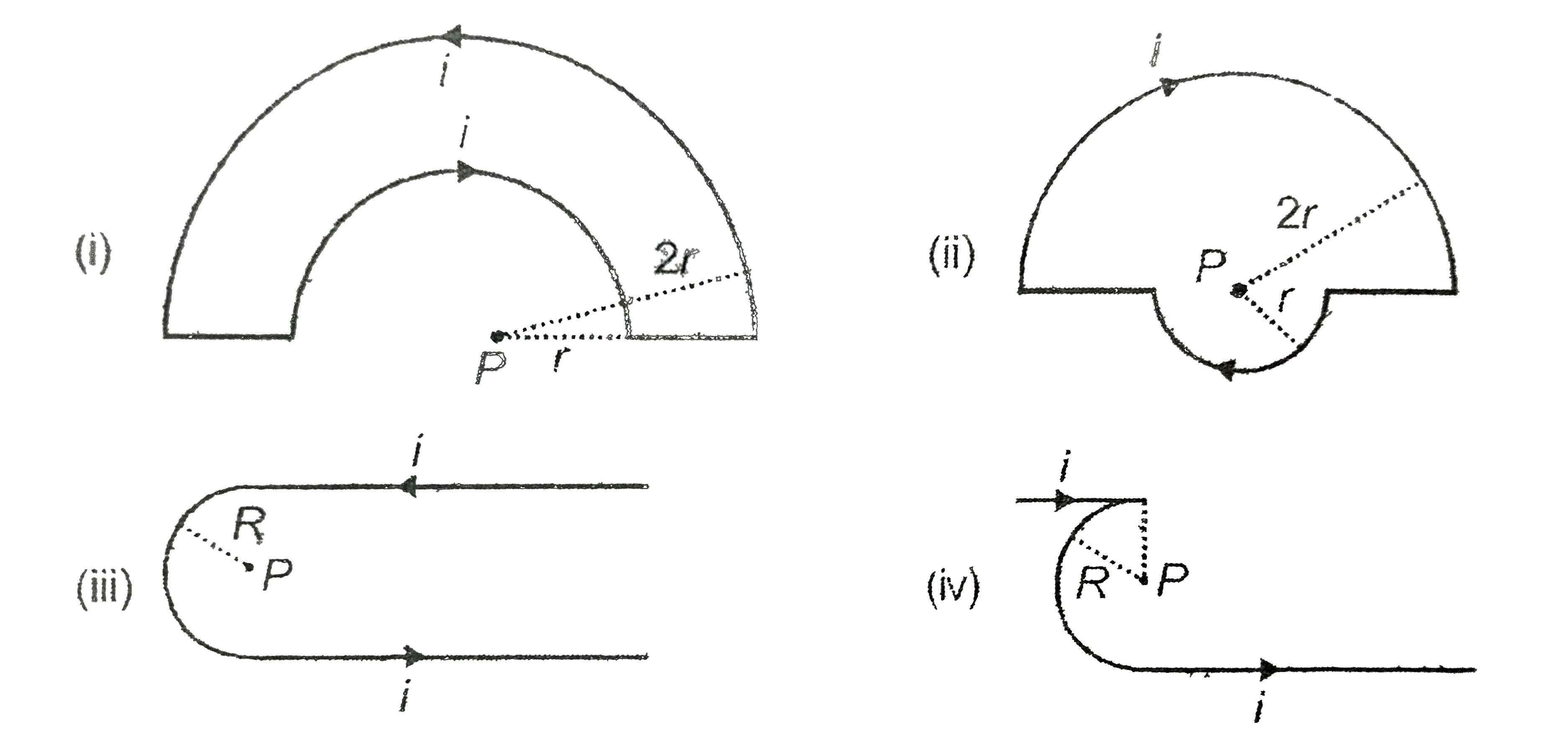
Find magnetic field at point P shown in Fig. point P is on the bisector of angle between the wires.
Assume PO=x,soPQ=xsin(α/2)
Magnetic field B at P due to either segment of wire is
B=μ0I4πxsin(α/2)[1+cosα2]
Net magnetic field at P is
Bnet=μ0I2πxsin(α/2)[1+cos(α/2)]
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.2
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example
20 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
Knowledge Check
Find the magnetic field at the origin in the fig. Shown in fig.
 Aμ0I4R(34ˆk+1πˆj)Bμ0I4R(32ˆk+1πˆj)Cμ0I4R(34ˆk+12πˆj)DNone of these
Aμ0I4R(34ˆk+1πˆj)Bμ0I4R(32ˆk+1πˆj)Cμ0I4R(34ˆk+12πˆj)DNone of theseTwo identical short magnets having magnetic moment M are placed perpendicular to each other with their , centres coniciding as shown in adjacent figure . The magnitude of the magnetic field at a point P at distance 'd' on the bisector of right angle will be .
 A√2μ0M4πd3B2√2μ0M4πd3C2μ0M4πd3D√3μ0M4πd3
A√2μ0M4πd3B2√2μ0M4πd3C2μ0M4πd3D√3μ0M4πd3
Find the magnetic field B at the point P in figure
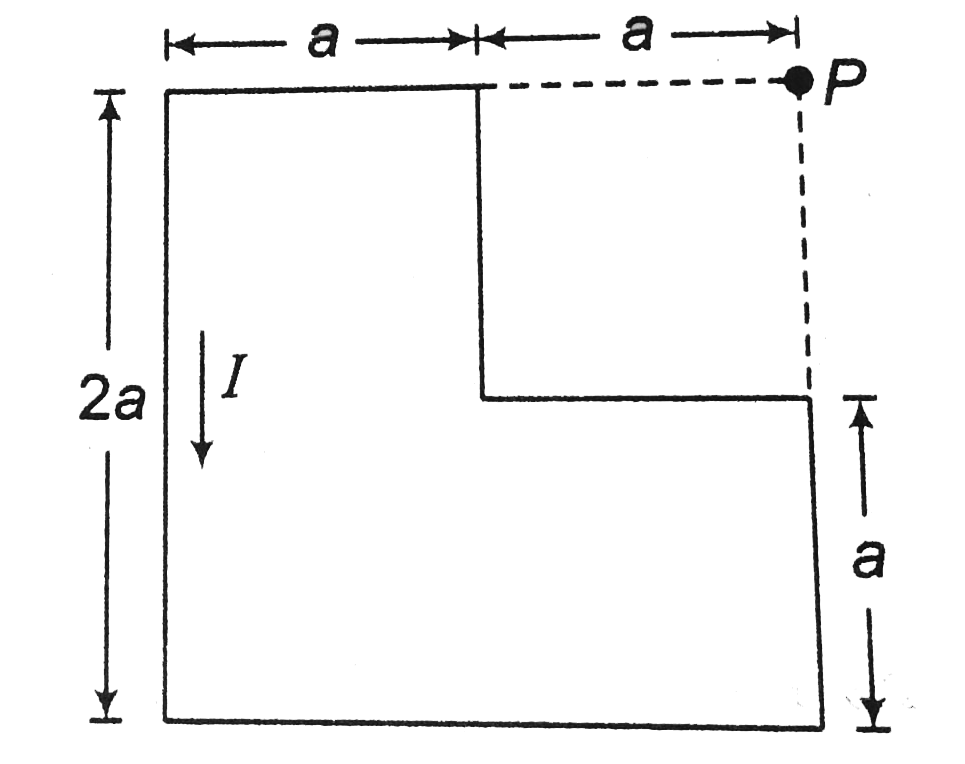
View SolutionIn Fig, find the magnetic field at point P.

View SolutionCurrent I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.

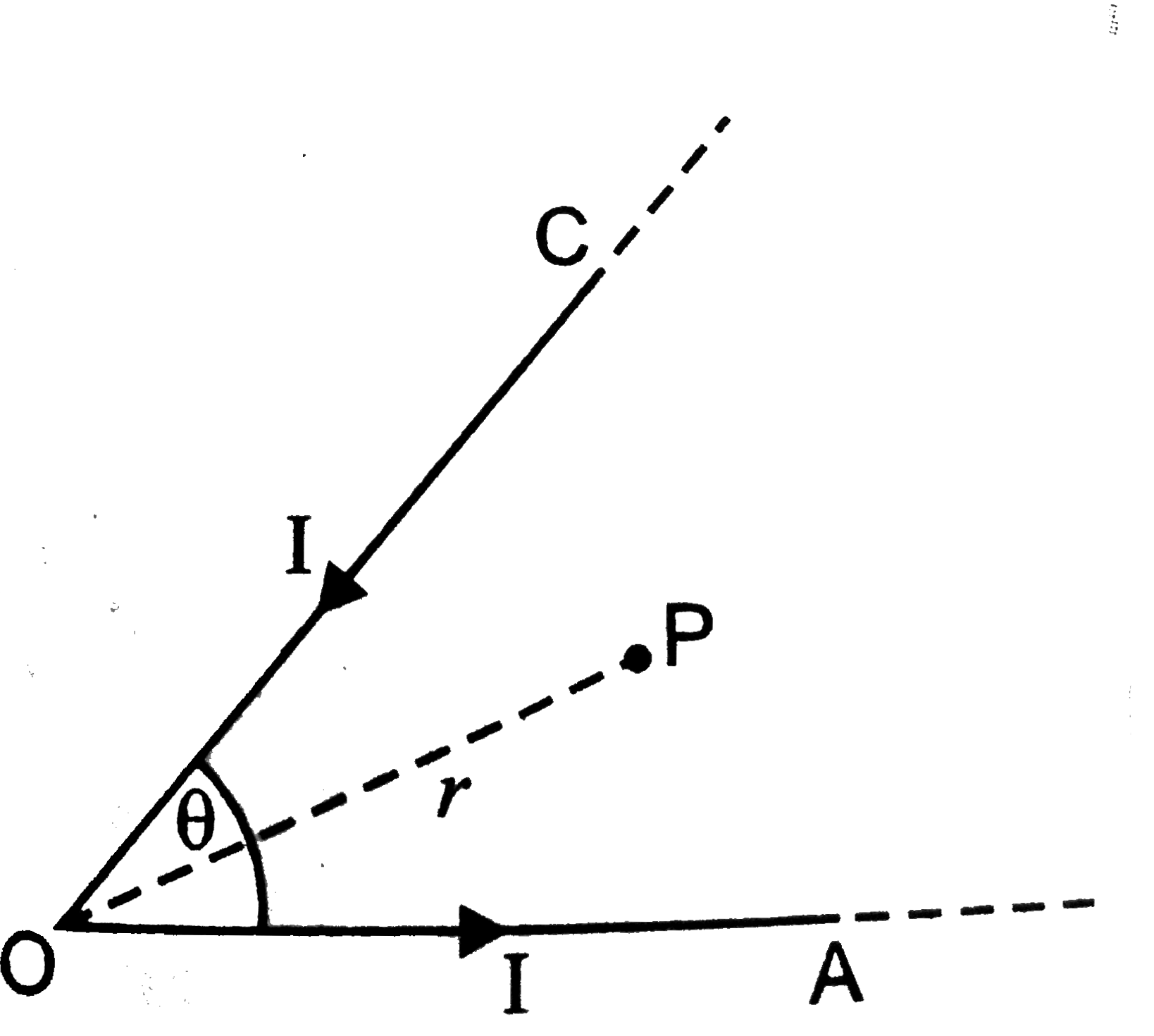
View SolutionTwo wires CO and OA carry equal currents I as shown in figure. One end of both the wires extends to infinity. Given ∠AOC=θ. What is the magnitude of magnetic field induction at a point P at a distance r from O lying on the bisector of angle θ.
View SolutionCalculate the magnitude of the magnetic field at point P as shown in Fig, in terms of R,I1andI2.

View SolutionFind magnitude and direction of magnetic field at point P in the following cases.
(a)
(b)
P is the centre of square.
(c)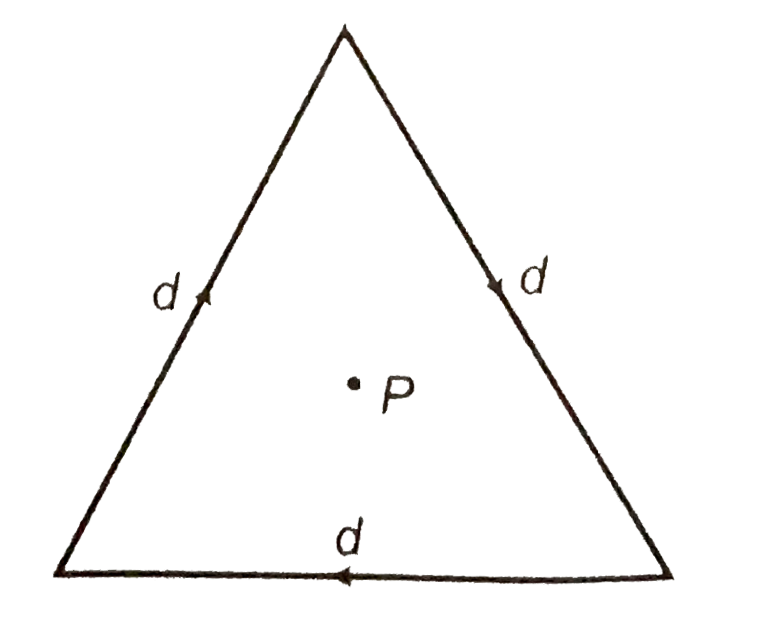
P is the centre of equilateral triangle.
(d)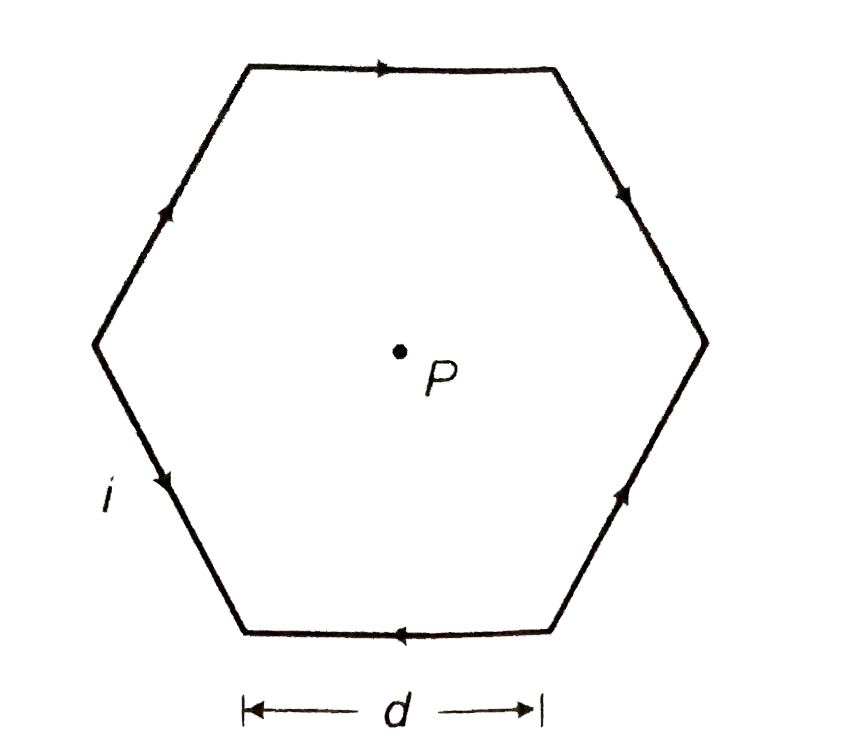
P is the centre of regular hexagon.
(e)
P is the centre of rectangular loop.
(f)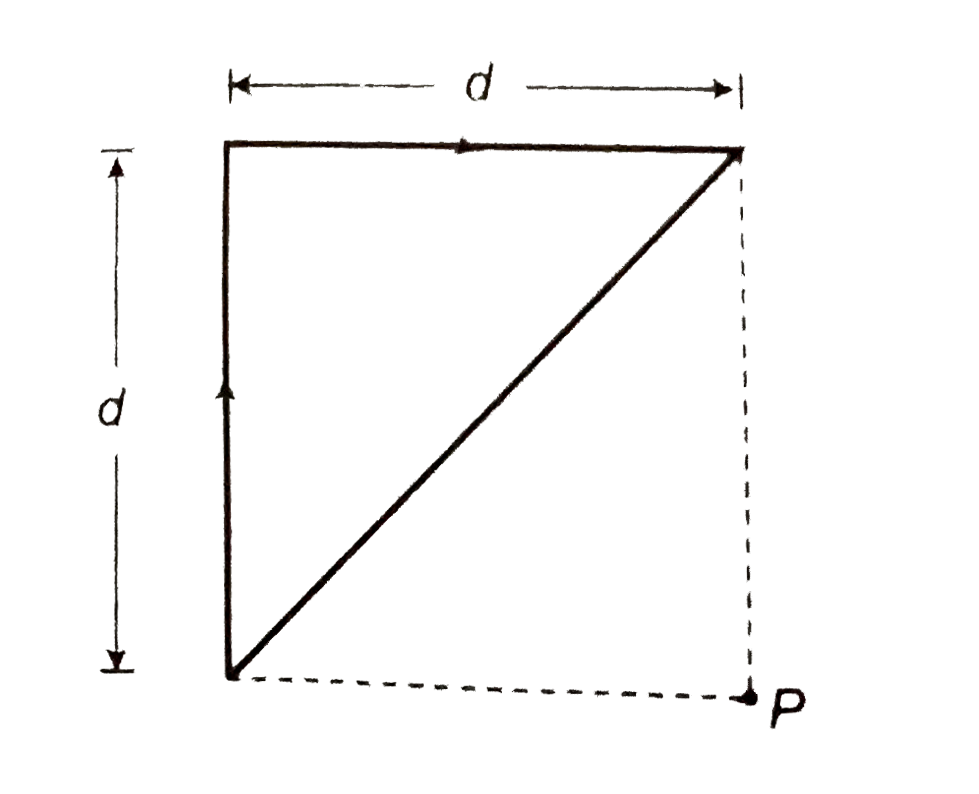
(g) A long wire carrying a current i is bent to from a plane angle θ. Find magnetic field at a point on the bisector of this angle is situated at a distance d from vertex.

(h) A long, straight wire carriers a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the sector. Let B2 be the magnetic field at this point due to this section only. find the value of d/l so that B2 differes from B1 by 1%.
View Solution