Let two long parallel wires, a distance d apart, carry equal currents I in the same direction. One wires at x=0, the other at x=d (as shown in Fig) Determine magnetic field at any point x-axis between the wires as a function of x.

Let us consider a point P at a distance (x,y) from the wire 1.

0≤x≤d
Hence →B1=μ0i2πxˆj
The point is at a distance d-x from wire 2.
∴→B2=μ0i2π(d−x)ˆj
∴→Bnet=→B1+→B2=μ0i2πxˆj≡μ0i2π(d−x)ˆj
→Bnet=(μ0i)(d−2x)2πx(d−x)ˆj
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.2
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example
20 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
Two long straight parallel wires A and B separated by a distance d, carry equal current I flowing in same direction as shown in the figure.
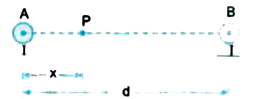
(a) Find the magnetic field at a point P situated between them at a distance x from one wire.
(b) Show graphically the variation of the magnetic field with distance x for 0<x<d.
View SolutionIn Fig. two long parallel wires (seen end-on) that are a distance R apart carry equal currents i in the same sense. Find the magnitude of the magnetic field at point P , which lies quidistant from the two wires at an angle θ from the plane of the wires.
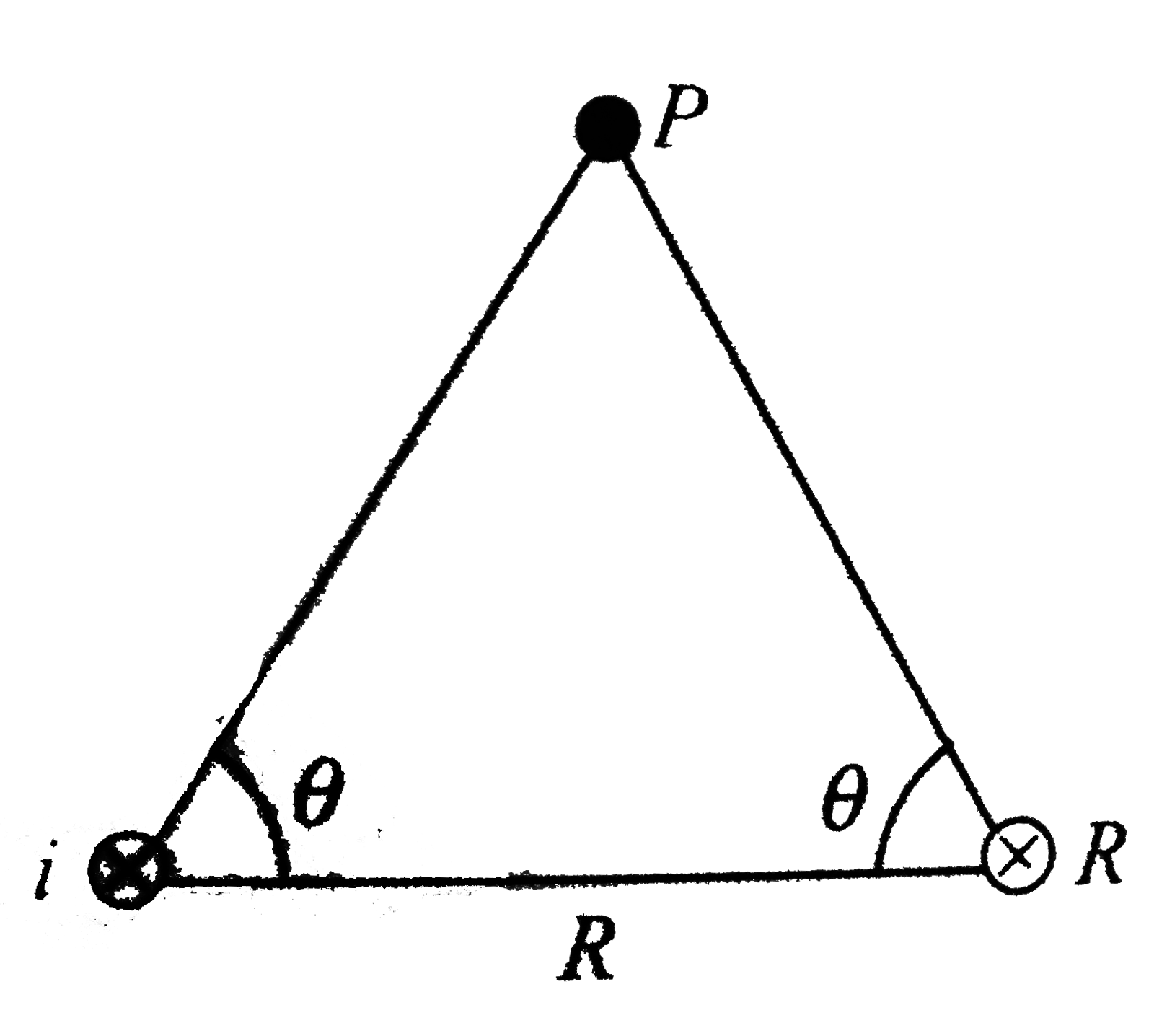
View Solution
Knowledge Check
Two thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
Arepel each other with a force of μ0i2/(2πd)Battract each other with a force of μ0i2/(2πd)Crepel each other with a force of μ0i2/(2πd2)Dattract each other with a force of μ0i2/(2πd2)Two infinitely long parallel wires carry equal currents in the same direction .The magnetic field at a mind point in between the two wires is
ASquare of the magnetic field produced due to each of the wiresBhalf of the magnetic field produced due to each of the wiresCtwice the magnetic field produced due to each of the wiresDzeroTwo long parallel wires are at a distance 2d apart. They carry steady equal currents flowing out of the plane of the paper , as shown. The variation of the magnetic field B along the line XX is given by
A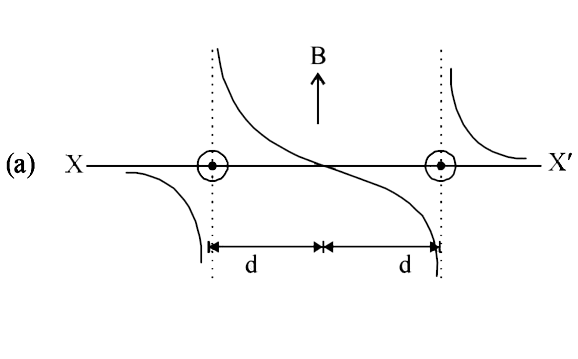 B
B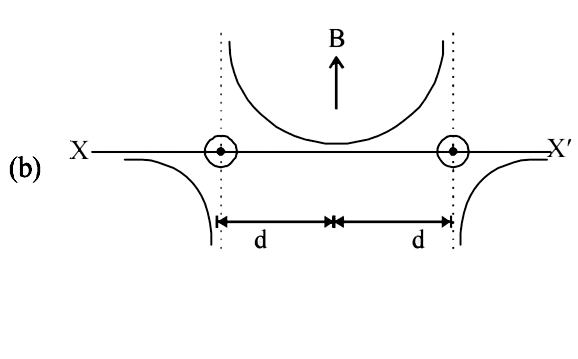 C
C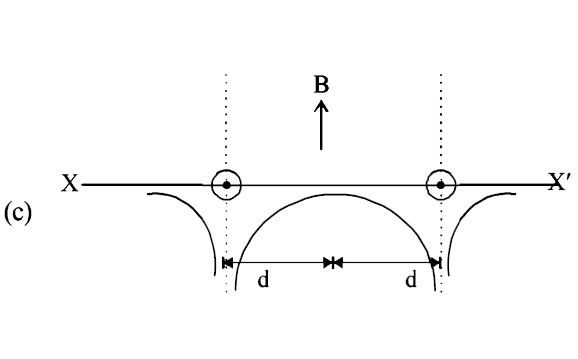 D
D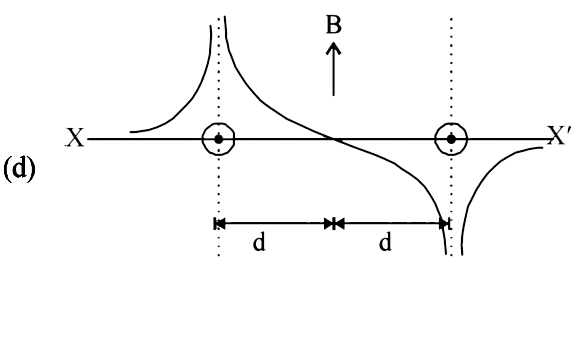
Two long parallel wires are at a distance 2d apart. They carry steady equal currents flowing out of the plane of the paper , as shown. The variation of the magnetic field B along the line XX is given by
View SolutionTwo infinitely long wires each carrying current I along the same direction are made into the geometry as shown in the figure. The magnetic field at the point P is

View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionTwo infinitely long parallel wires carry equal current in same direction. The magnetic field at a mid point in between the two wires is
View Solution
