Calculate the magnetic field at point O in each of the following cases:





Video Solution
Text Solution
Here straight and circular shape wires are joined, determine magnetic field for each shape and find resultant magnetic field. It should be kept in mind that magnetic field due to stright wire at any point along its length is zero.
(a) 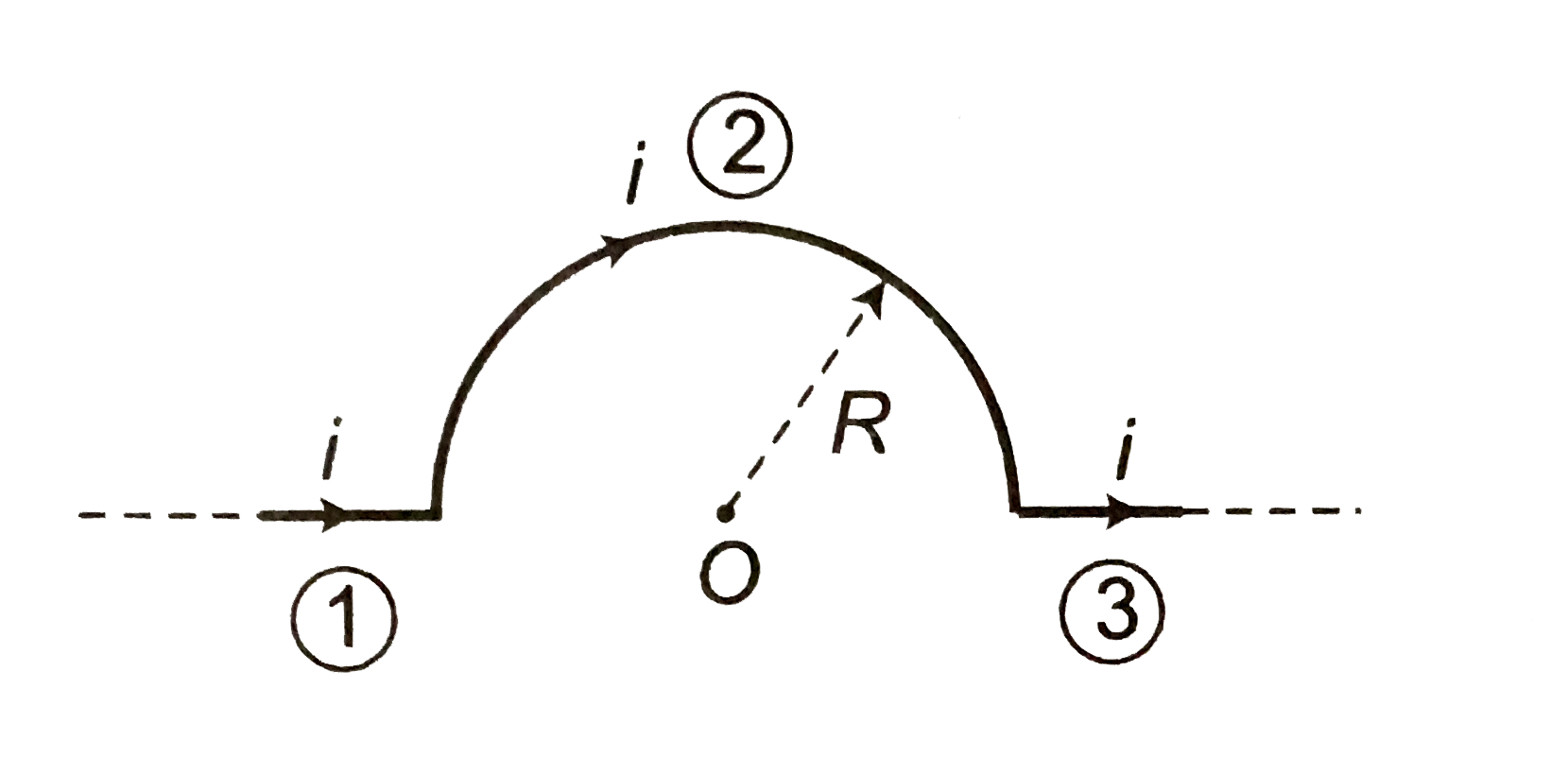
Since point is along the length of straight wires and hence
(b) 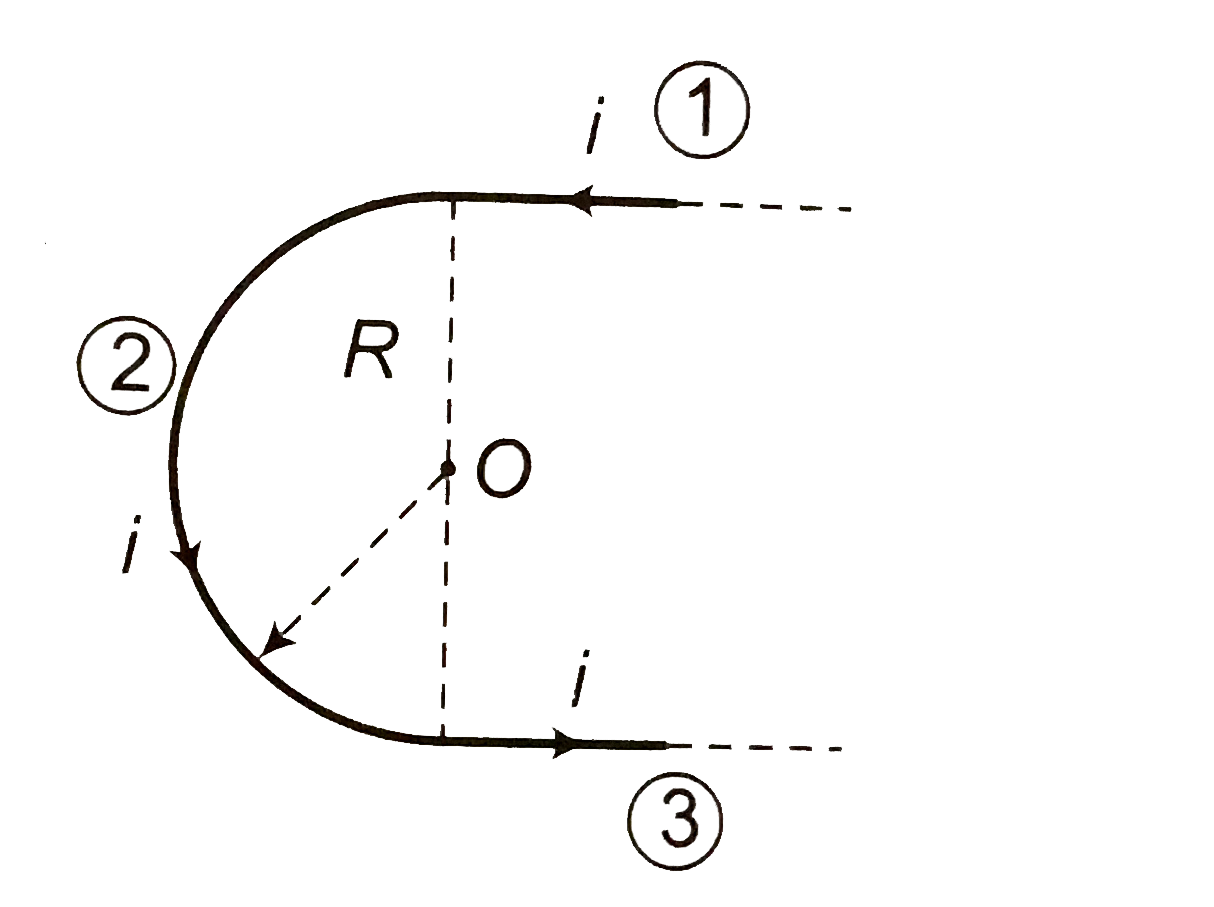
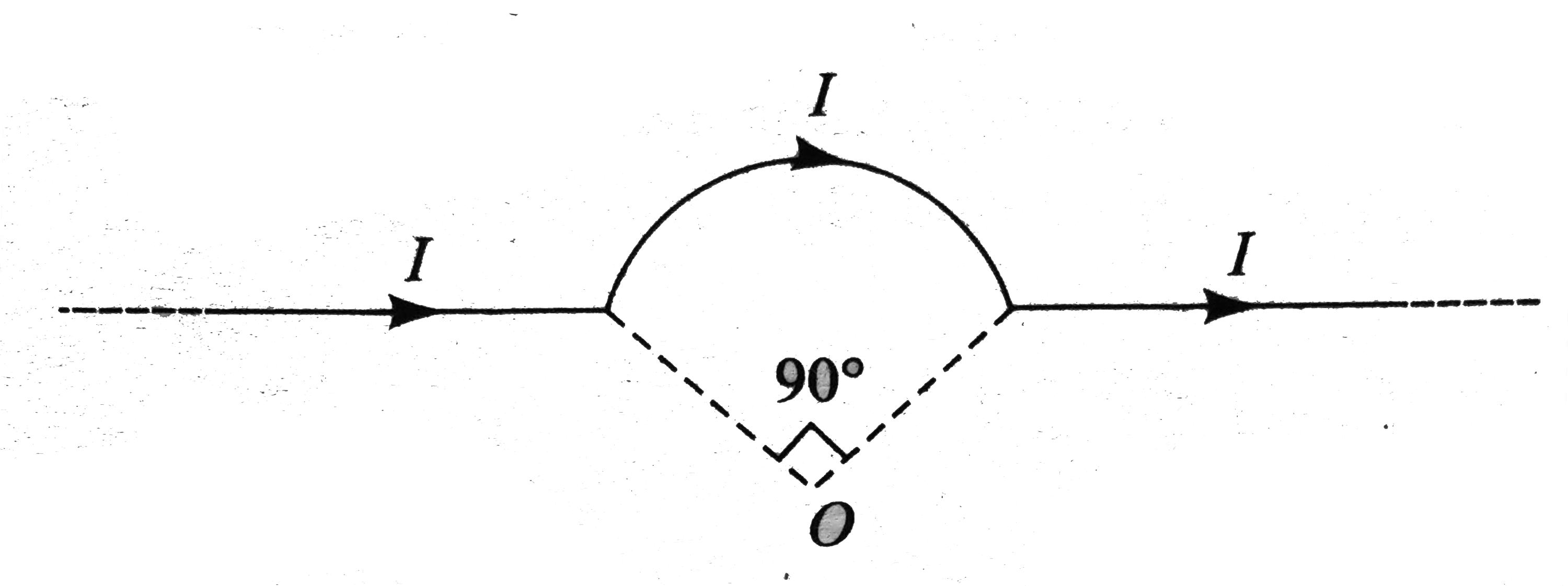
Point is the foot of long wires and
Due to semi-circle
(c) 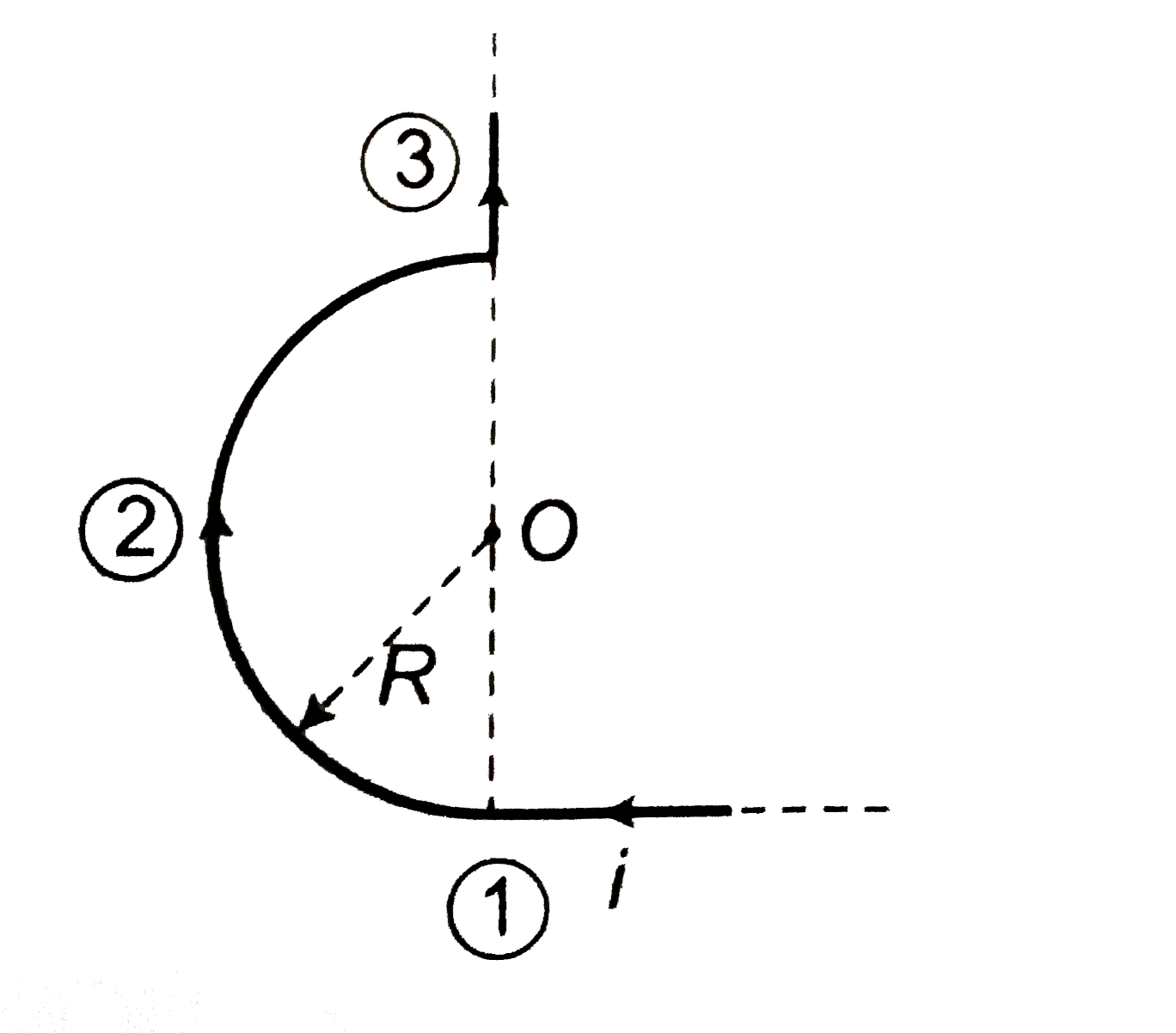
At :
(d) 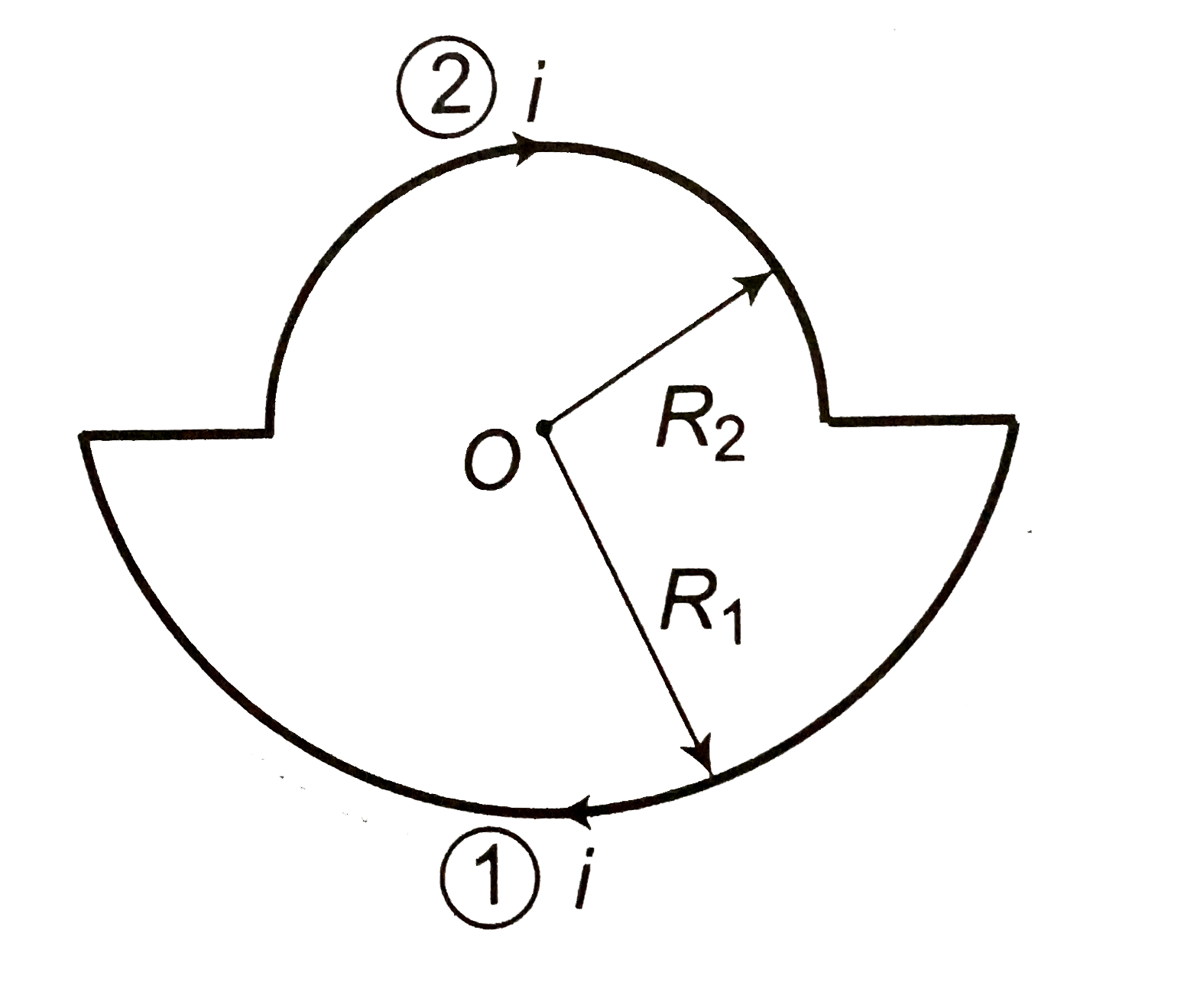
Magnetic field at due to straight wires is zero.
(e) 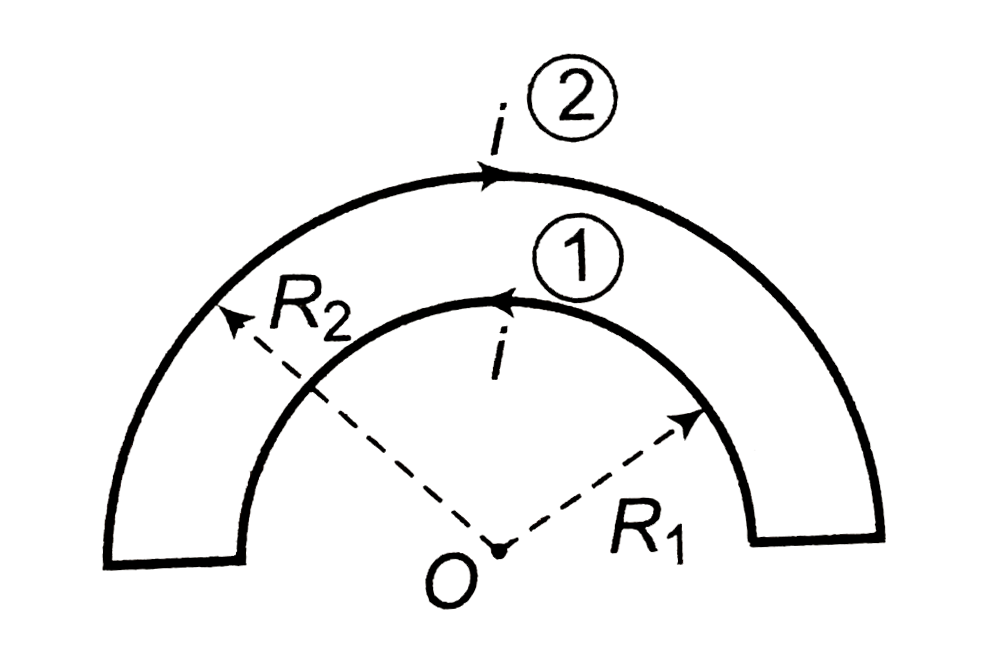
Magnetic field at due to straight wires is zero.
(f) 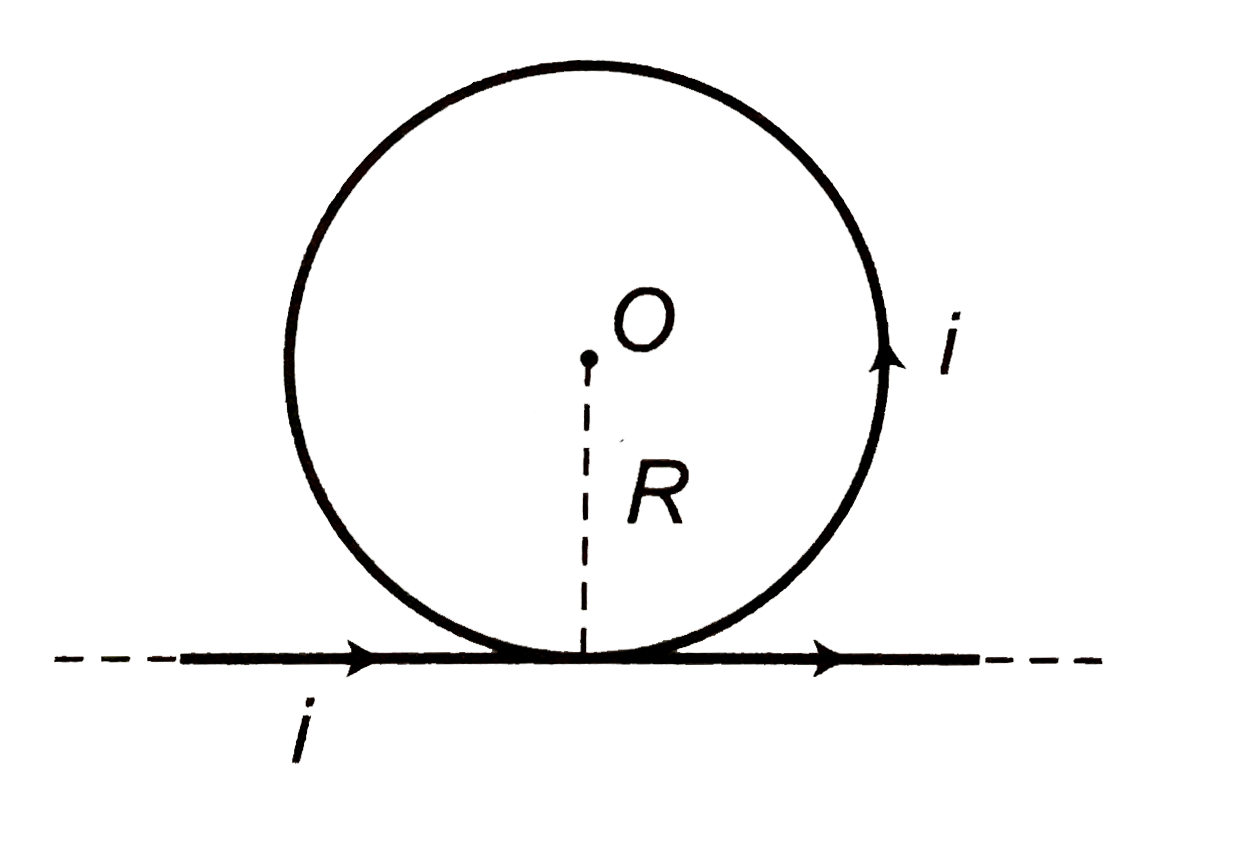
Due to straight wire
Due to circular wire
(g) 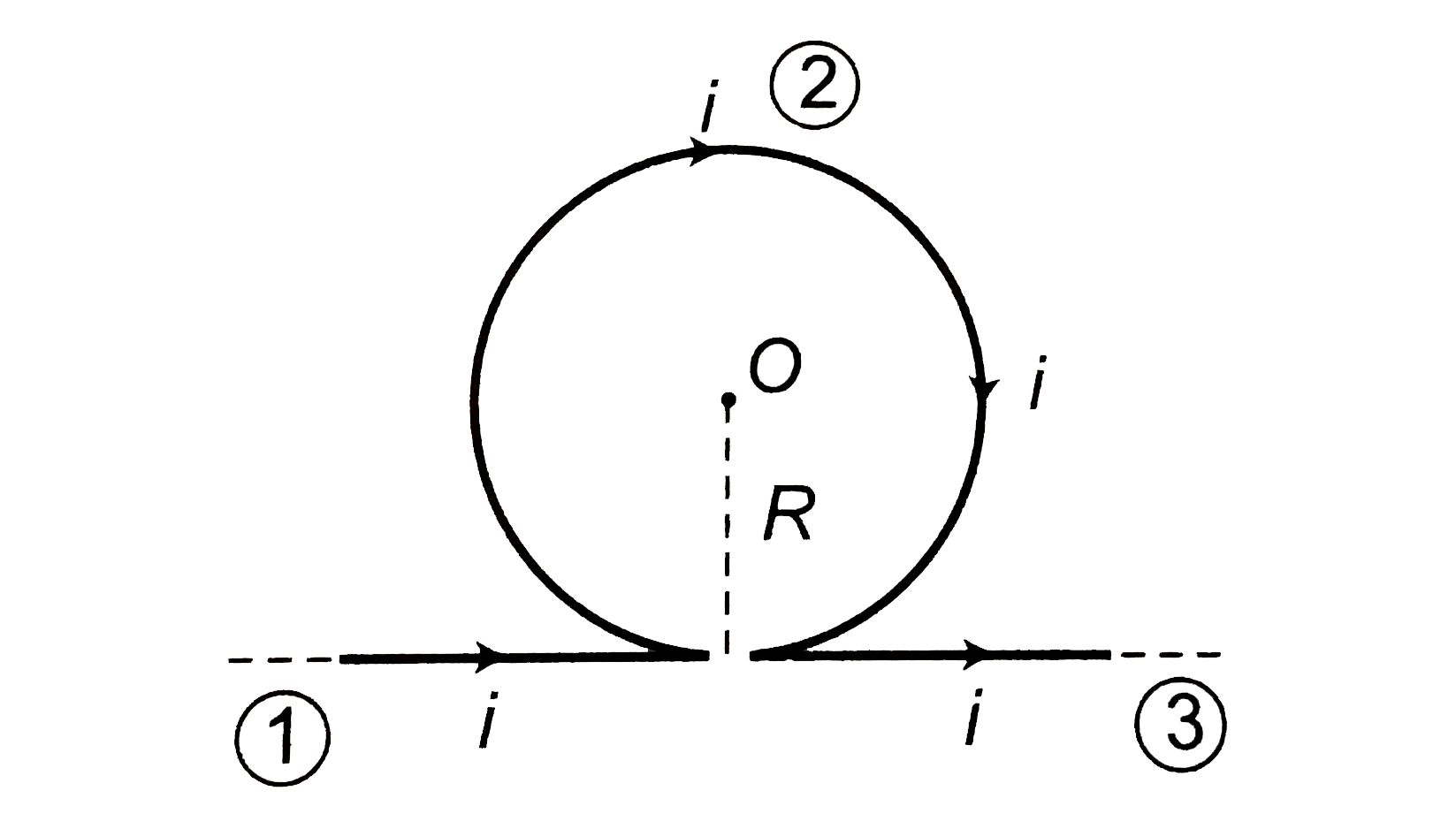
(h) 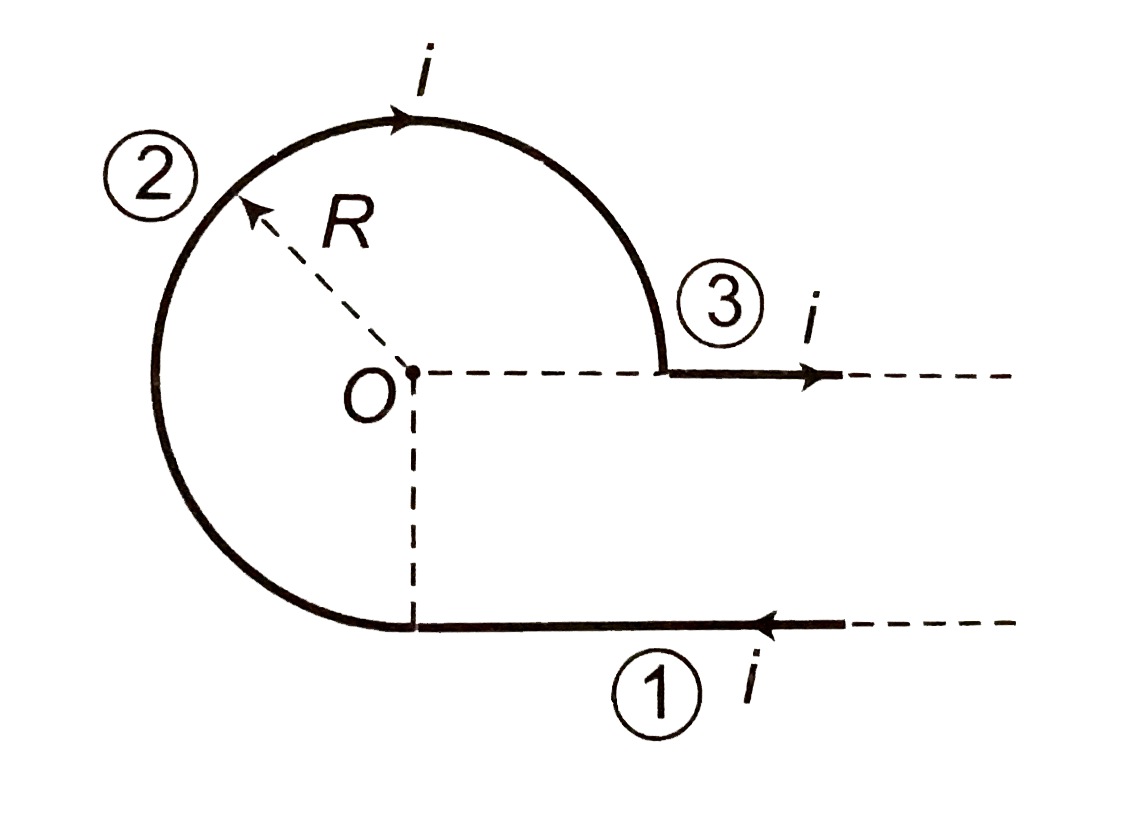
(i) 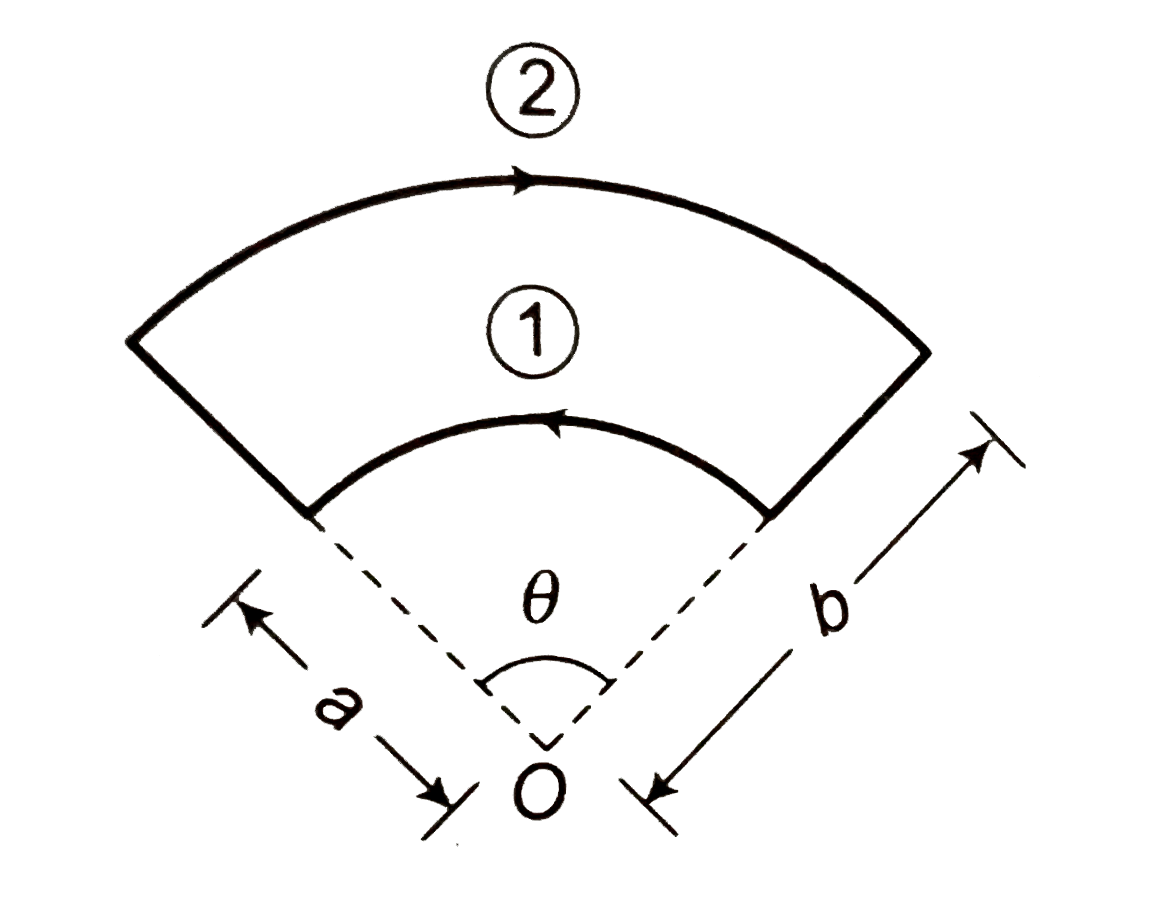
(j) 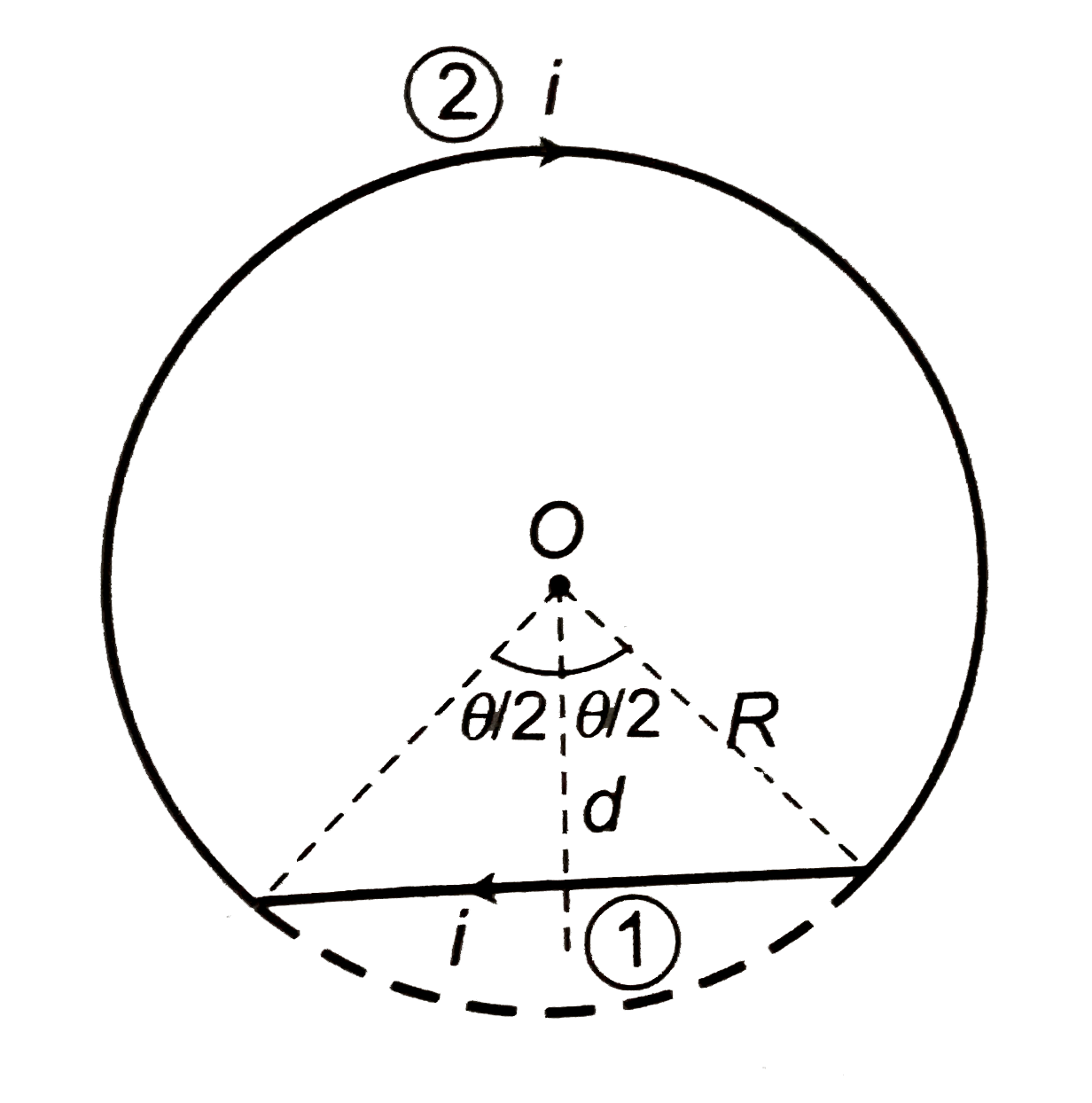
(k) 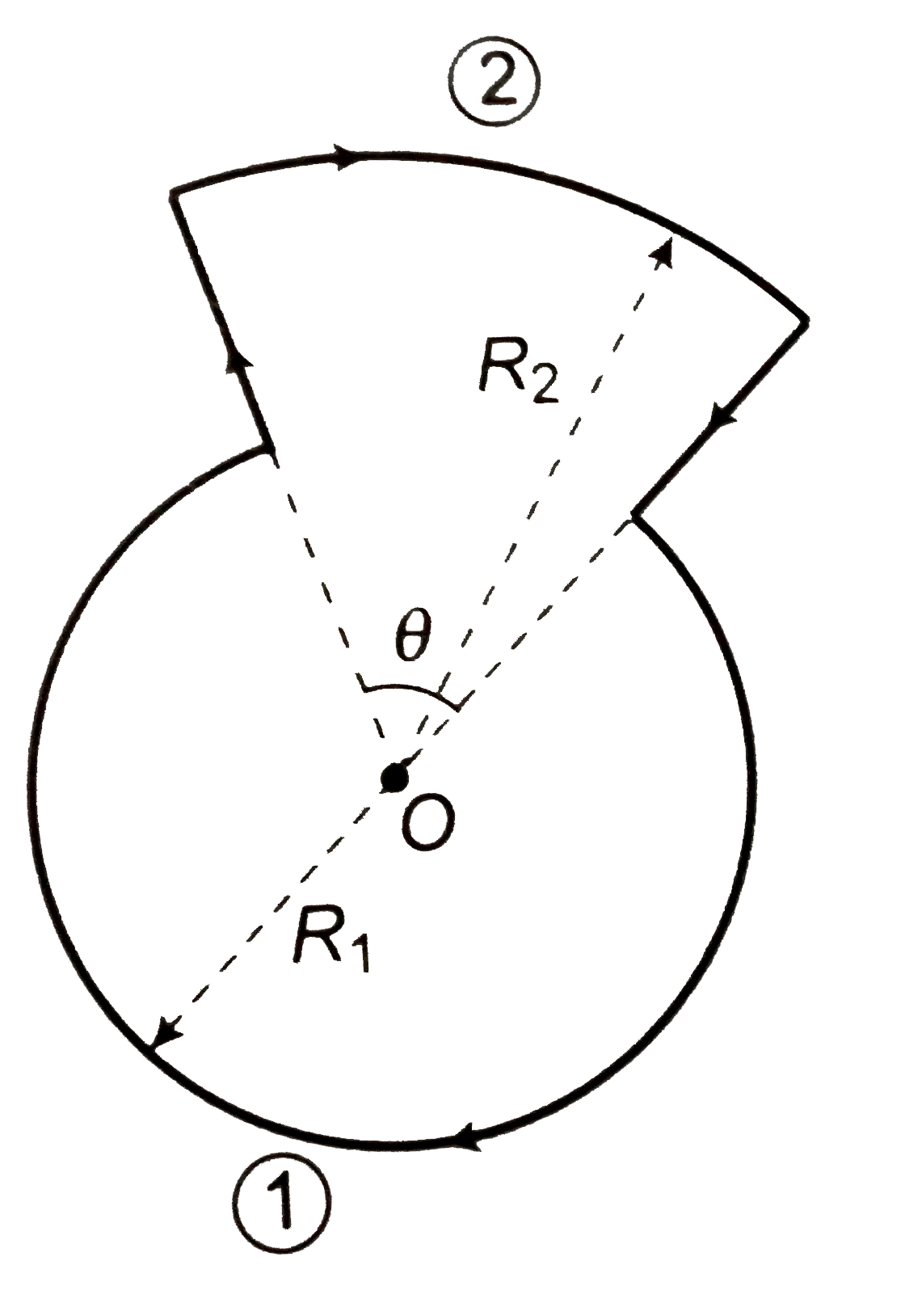
(l)
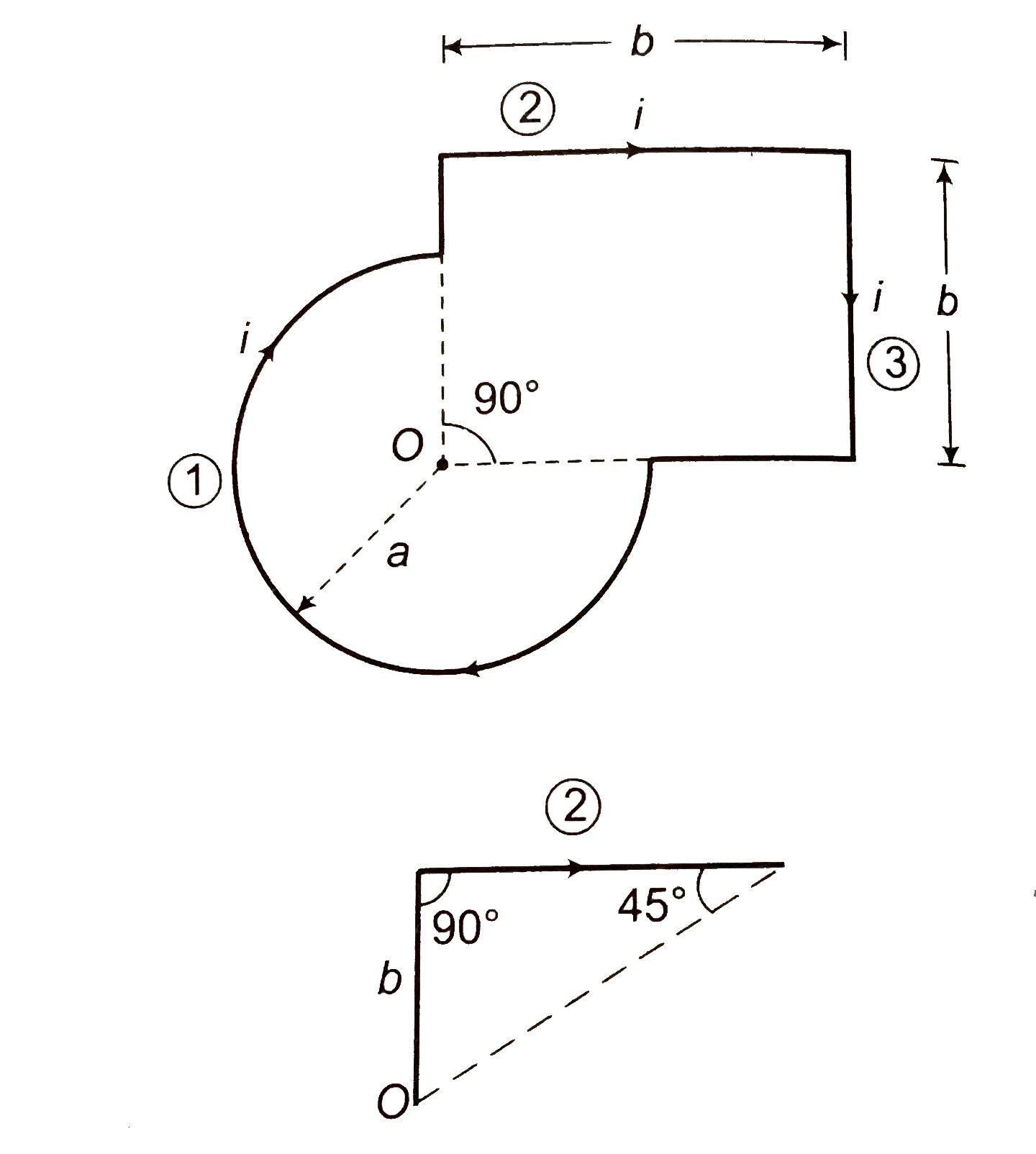

(m) 
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The magnetic field at O is
 Aμ0I2R√(14+1π2)Bμ0I2R√(12+1π2)Cμ0IR√(14+1π2)Dμ0IR√(14+1π)
Aμ0I2R√(14+1π2)Bμ0I2R√(12+1π2)Cμ0IR√(14+1π2)Dμ0IR√(14+1π)The magnetic field at O is
 AzeroB1C2D3
AzeroB1C2D3Find magnetic field at O.
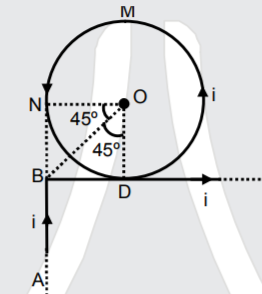 Aμ0i2πR[−1√2+π]Bμ0i2πR[π−1]Cμ0i2RDμ0i2πR[1√2+π]
Aμ0i2πR[−1√2+π]Bμ0i2πR[π−1]Cμ0i2RDμ0i2πR[1√2+π]
Find the magnetic field at point P in following cases
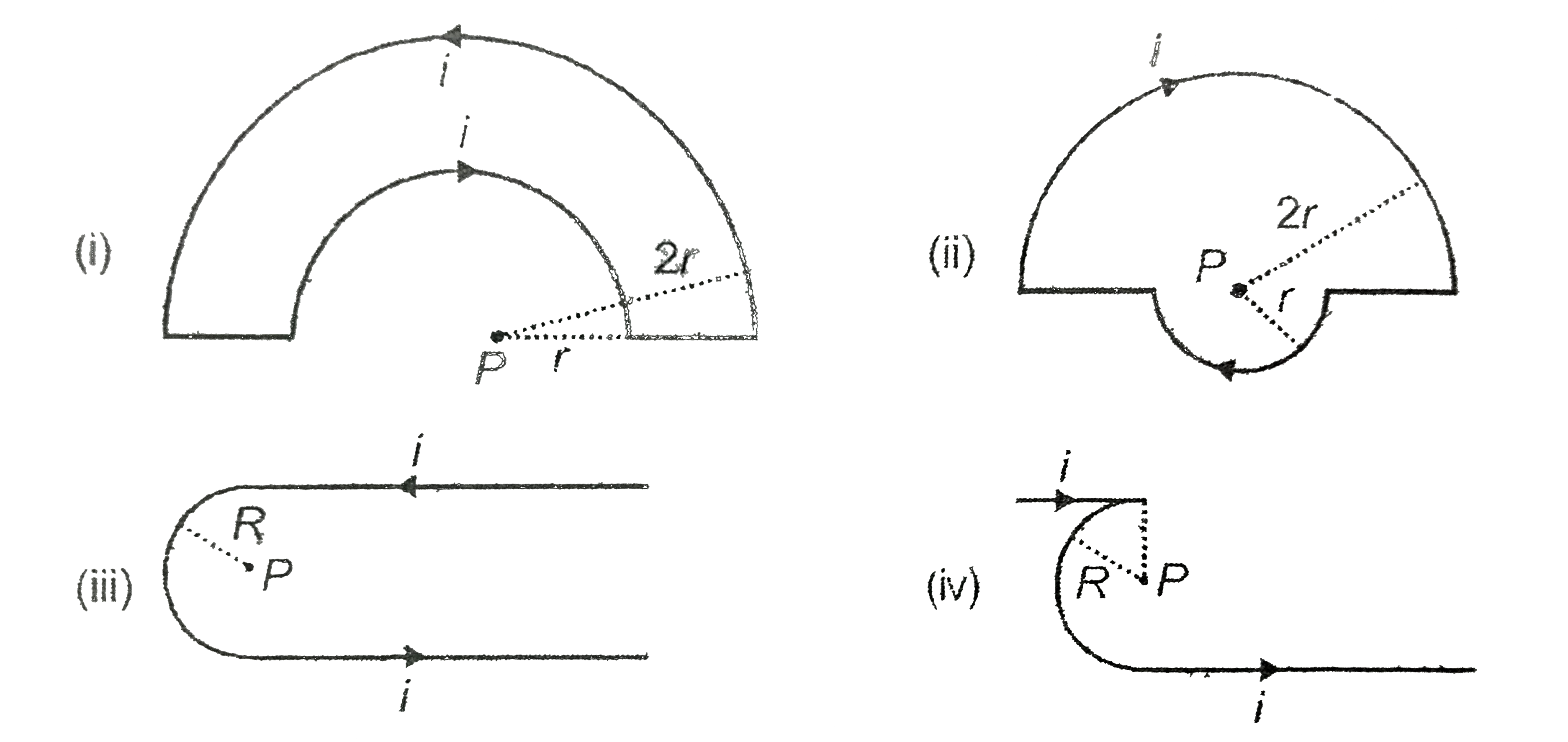
View SolutionFind the magnetic field at point O shown in the figure

View SolutionEvaluate magnitude and direction of magnetic field at a point P in the following cases
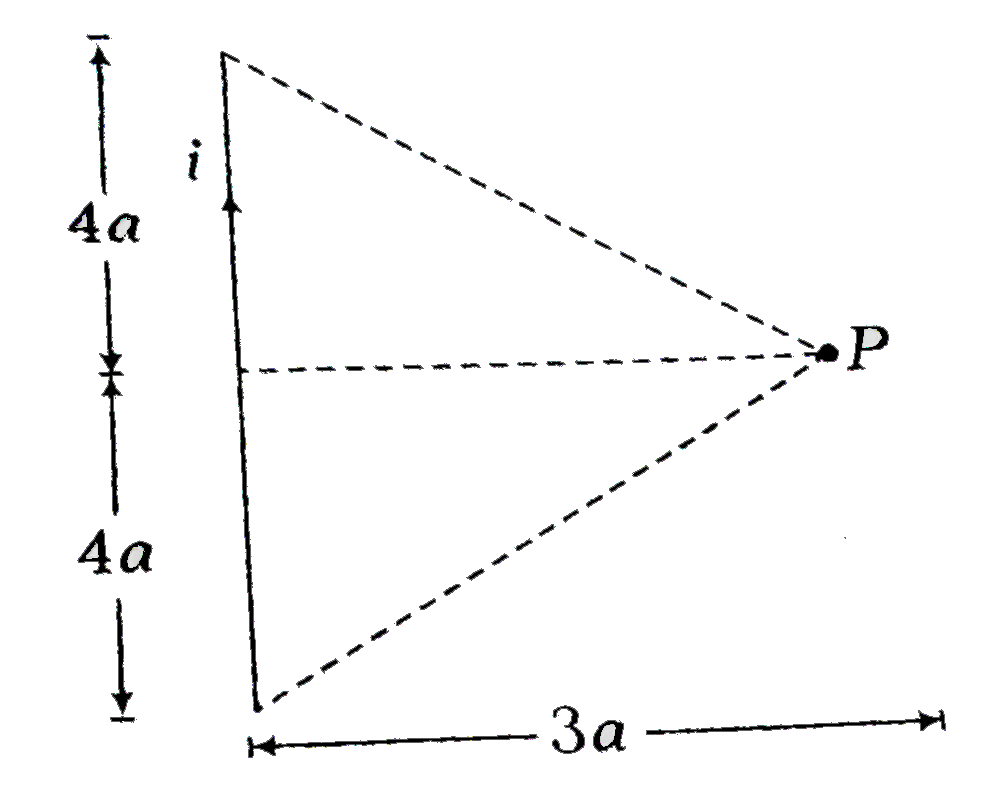

View SolutionMagnetic field at point O due to the given structure is
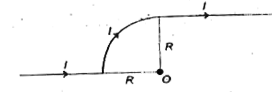
View SolutionThe magnetic field at centre O of the arc in Fig.
View Solution

