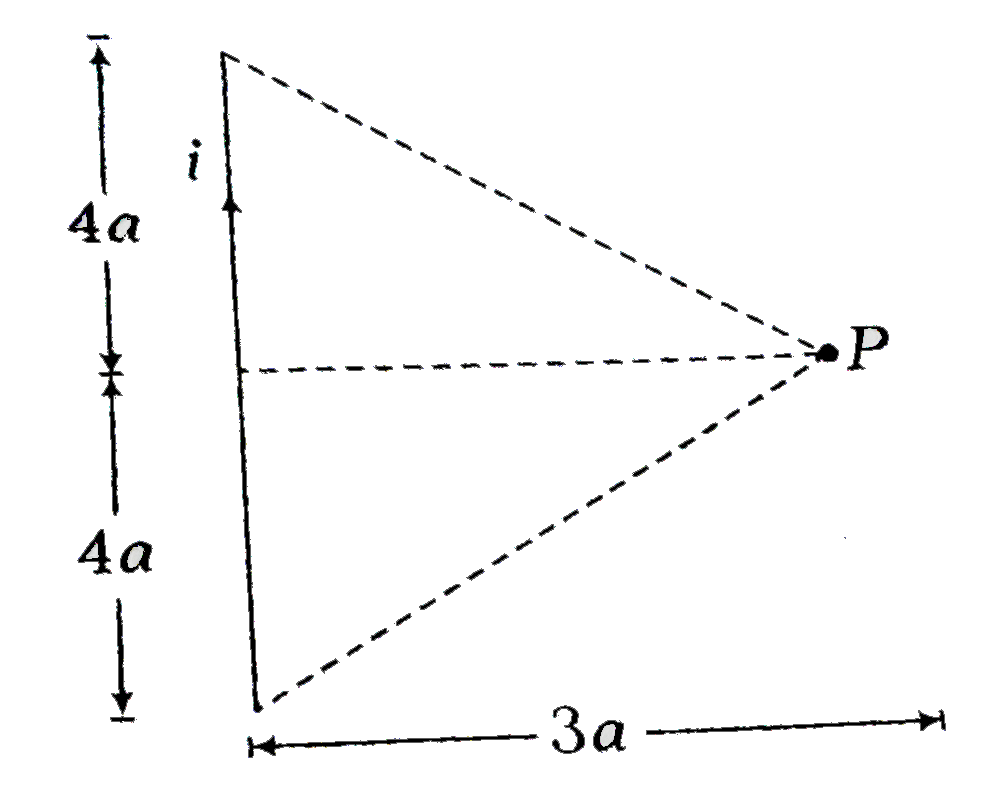
Find magnitude and direction of magnetic field at point P in the following cases.
(a) 
(b) 
P is the centre of square.
(c) 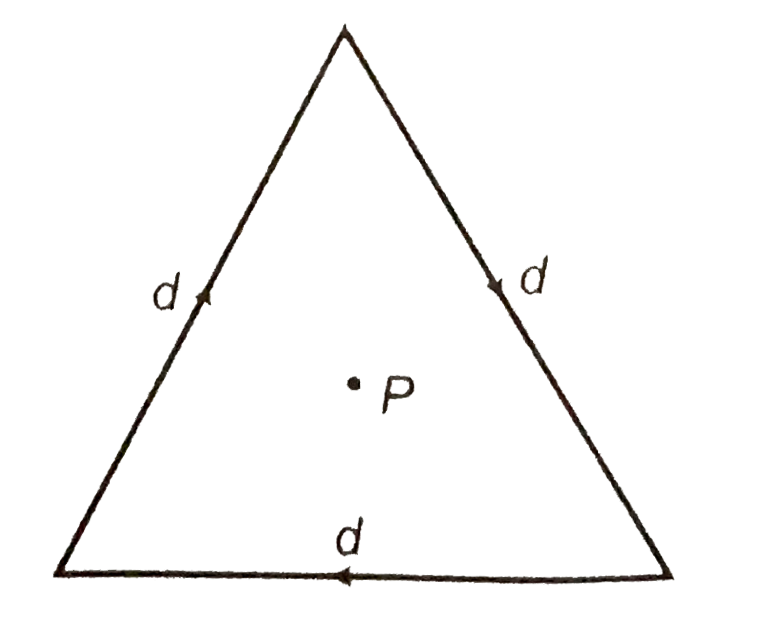
P is the centre of equilateral triangle.
(d) 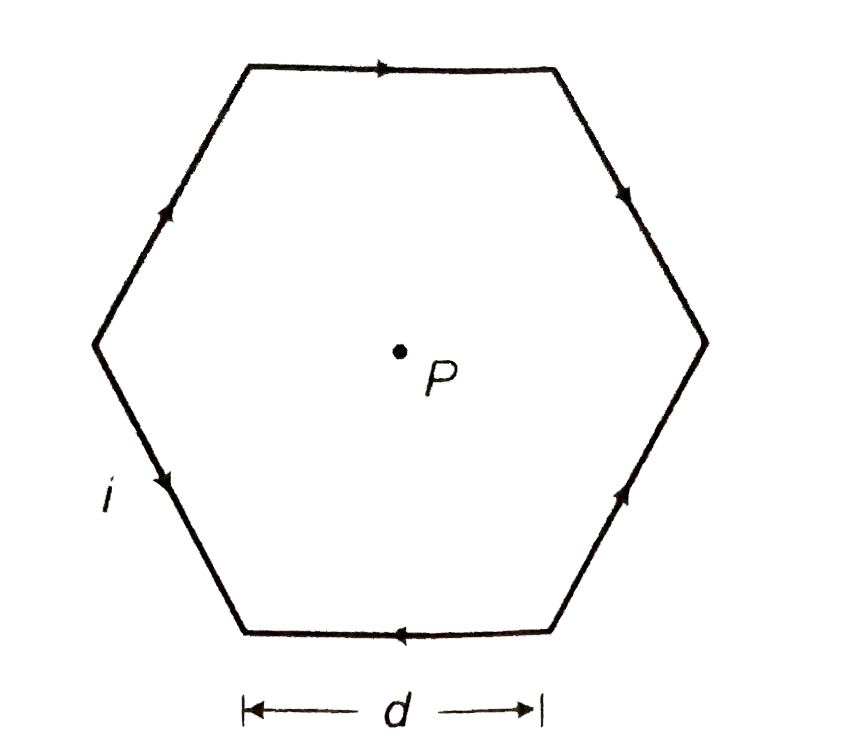
P is the centre of regular hexagon.
(e) 
P is the centre of rectangular loop.
(f) 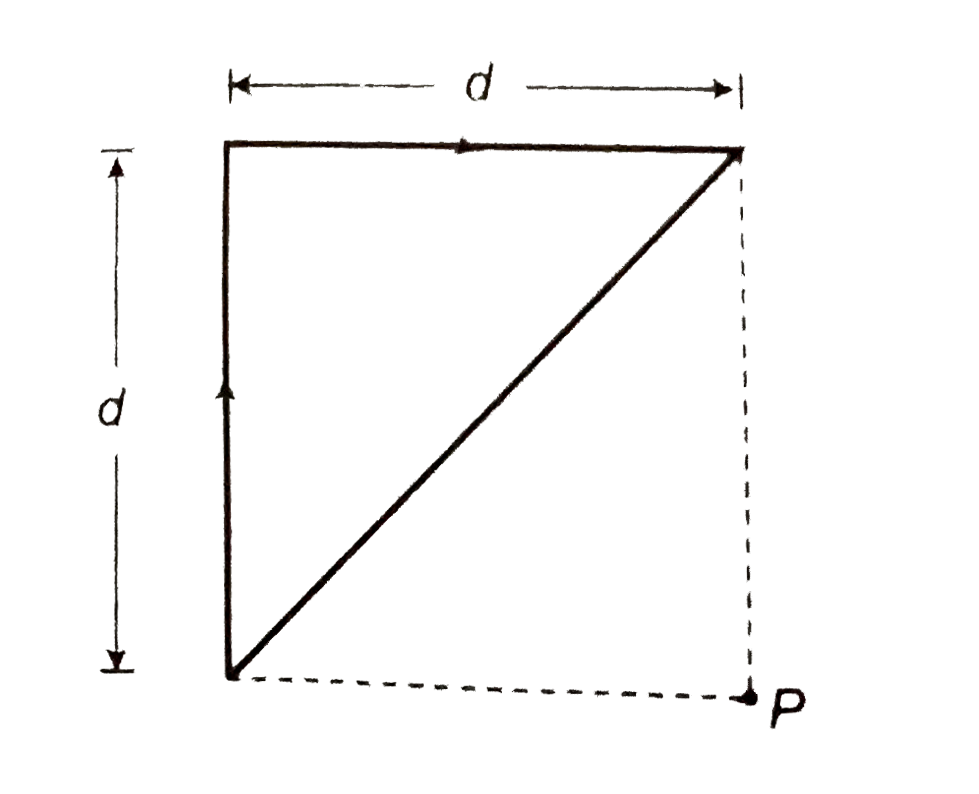
(g) A long wire carrying a current i is bent to from a plane angle θ. Find magnetic field at a point on the bisector of this angle is situated at a distance d from vertex.

(h) A long, straight wire carriers a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the sector. Let B2 be the magnetic field at this point due to this section only. find the value of d/l so that B2 differes from B1 by 1%.
Text Solution
(a) 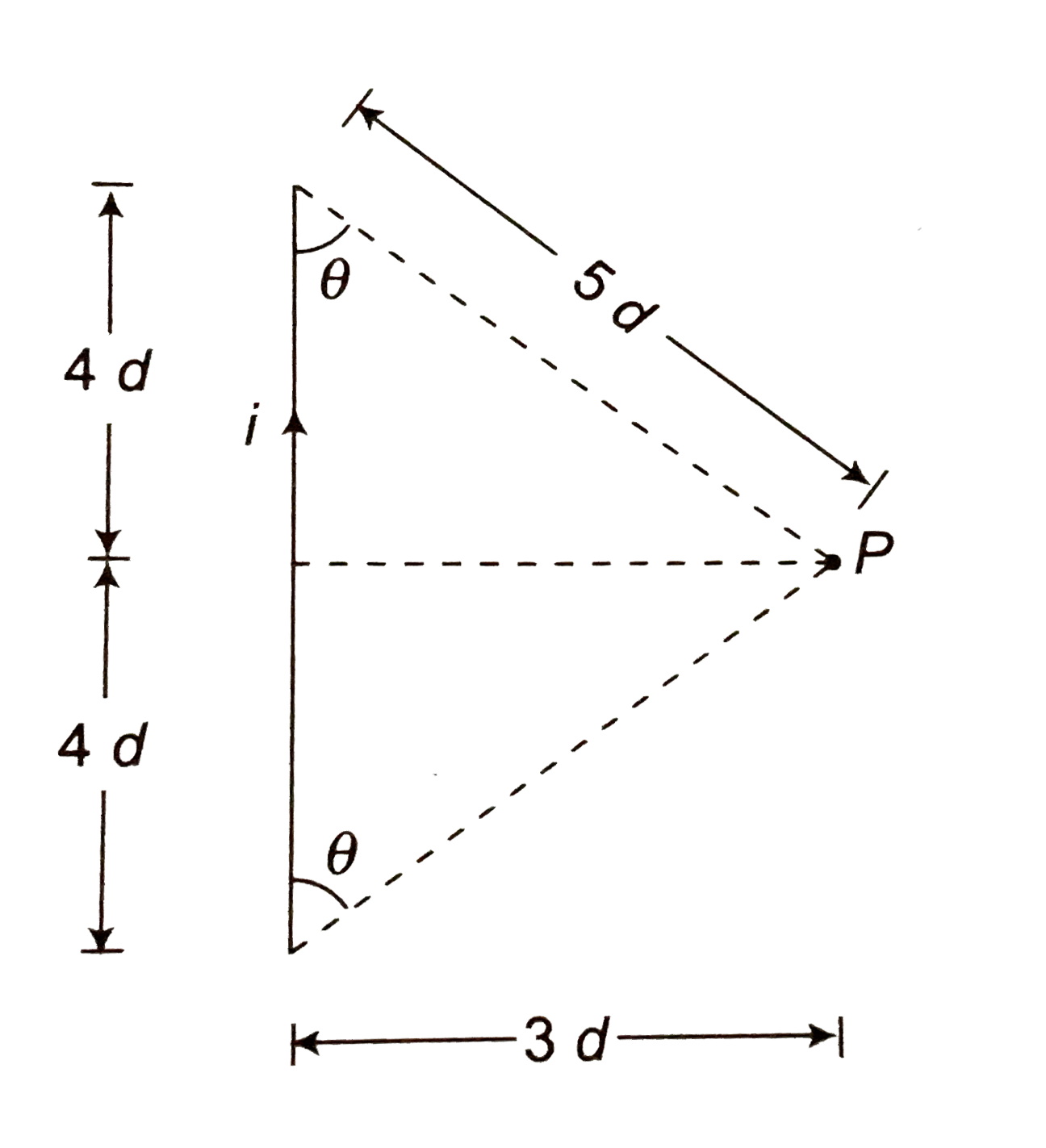
BP=μ0i4πd'[cosθ1+cosθ2]
=μ0i4π(3d)[cosθ+cosθ]
=μ0i6πdcosθ
cosθ=45
BP=μ0i6πd.45=2μ0i15πd⊗.
(b) 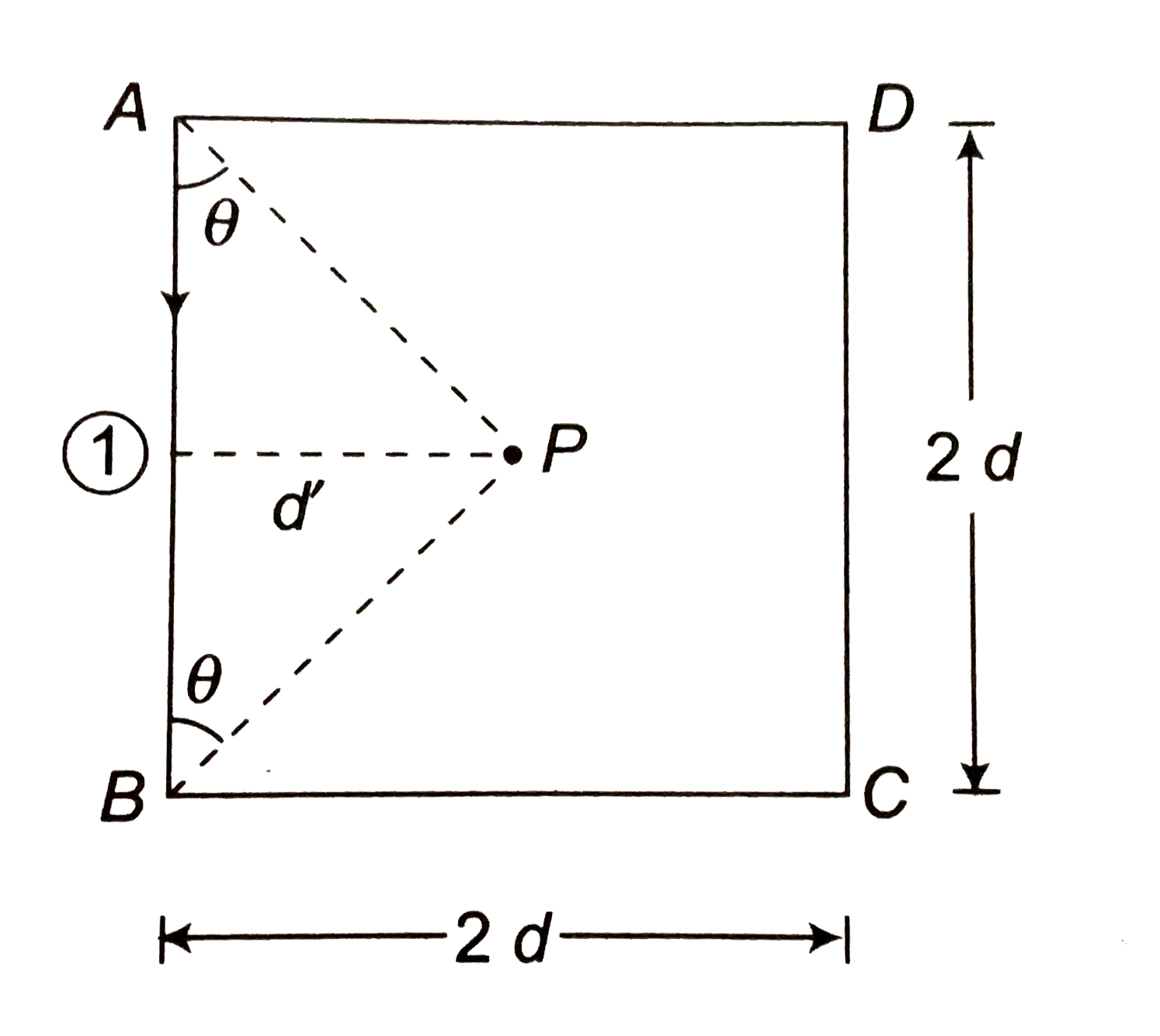
Magnetic field at P due to one side of square, say AB
B1=μ0i4πd'(cosθ+cosθ)
d'=d,θ=45∘
=μ0i4πd.2.1√2=μ0i2√2πd
Magnetic field due to square loop
Bp=4B1=√2μ0iπd
Since current anticlockwise, magnetic field at P will be outside the plane of paper.
BP=√2μ0iπd,⊙
(c) 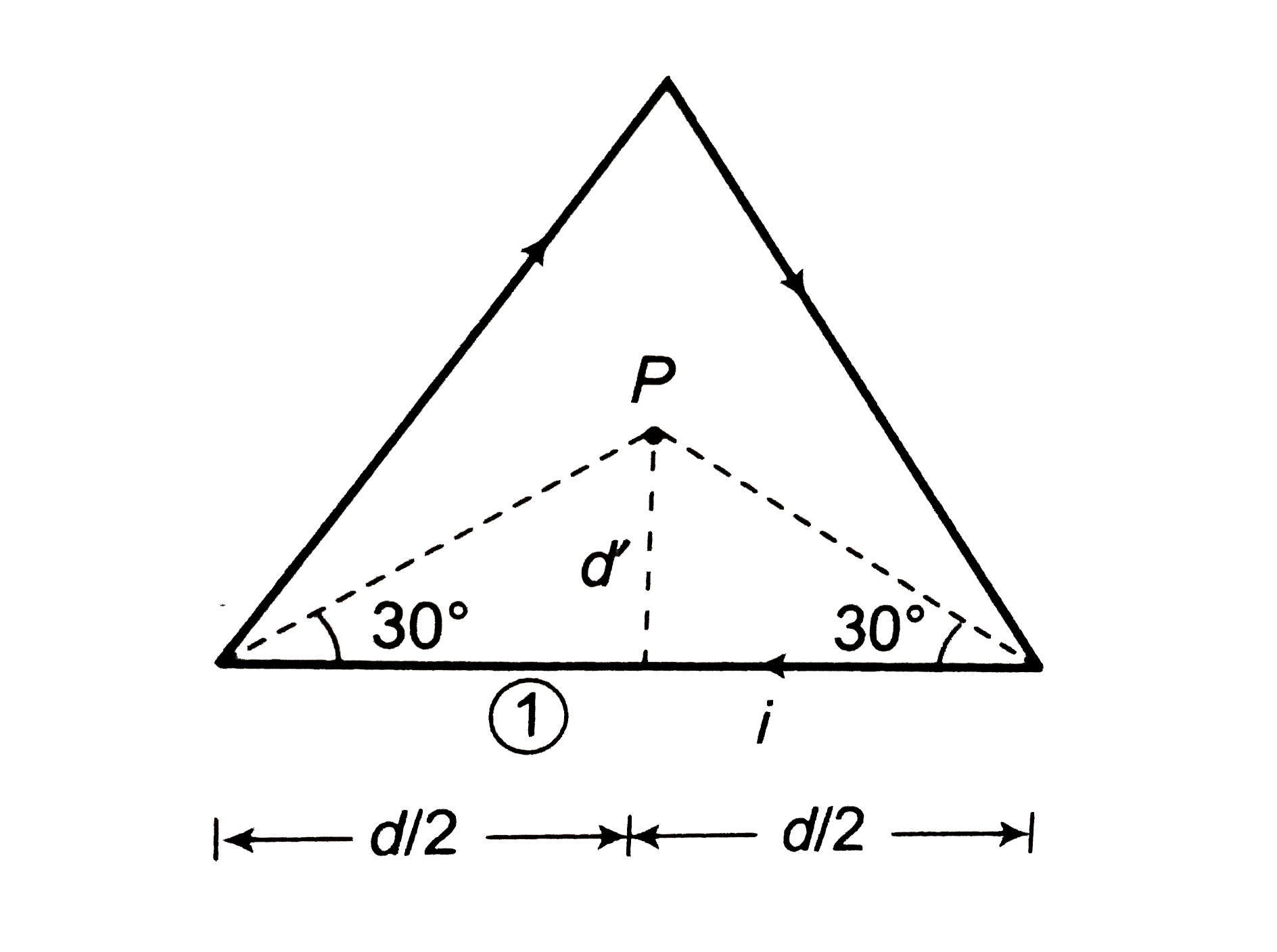
tan30∘=d'd/2⇒d'=d2√3
θ1=θ2=30∘
B1=μ0i4πd'[cos30∘+cos30∘]
=μ0i4π.d2√3.2√32=3μ0i2πd
Magnetic field at P due to triangular loop
BP=3B1=9μ0i2πd
Since current is clockwise, magnetic field at P inside the plane of paper.
Bp=9μ0i2πd
Since current is clockwise, magnetic field at P inside the plane of paper.
Bp=9μ0i2πd,⊗
(d) 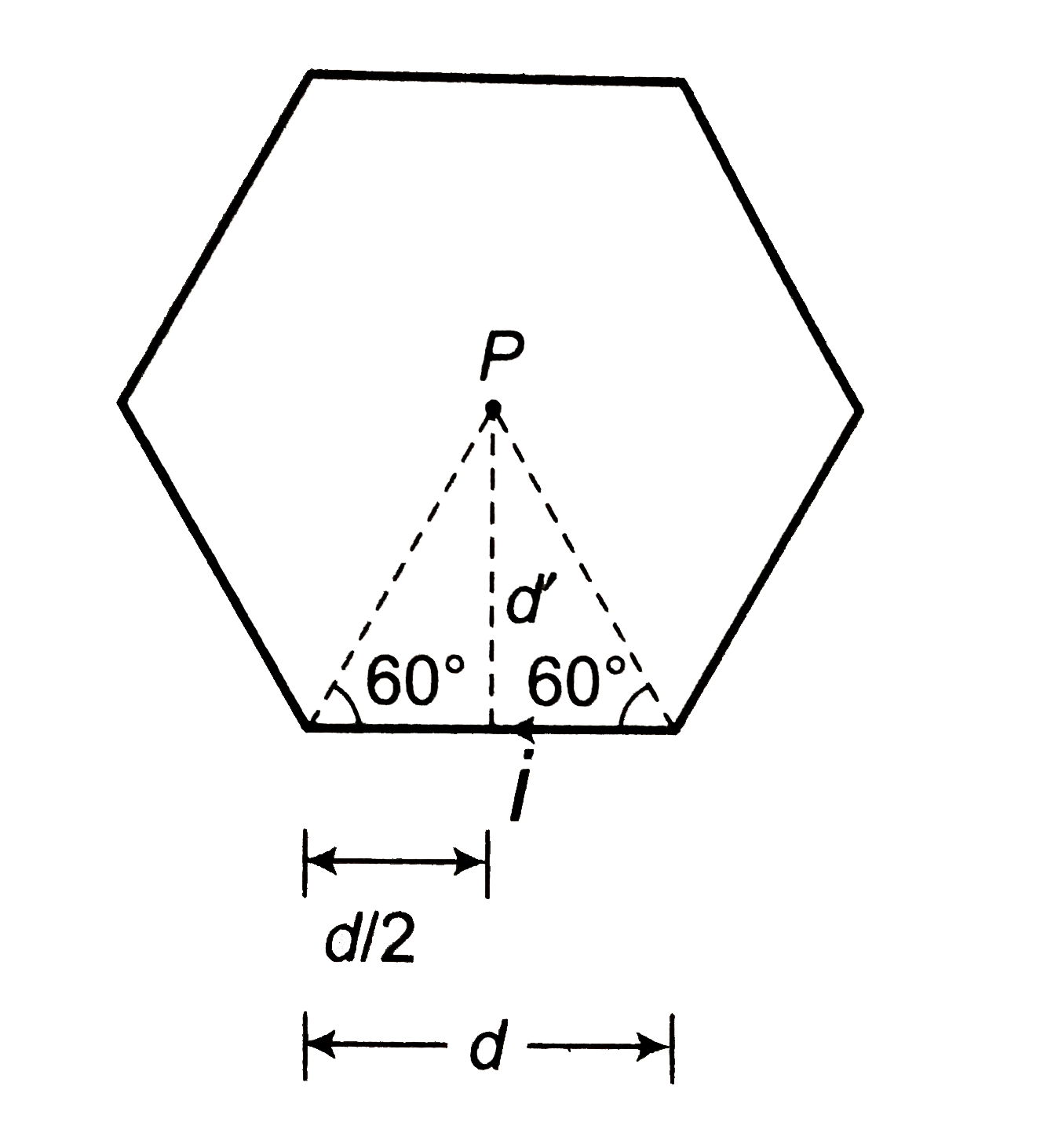
B1=μ0i4πd'(cos60∘+cos60∘)
=μ0i4π.d2tan60∘.2cos60∘
=μ0i2πd√3
BP=6B1=√3μ0iπd,⊗
(e) 
From △ADC,AC=10d
cosα=8d10d=45,cosβ=6d10d=35
d1=3d,d2=4d
B1=μ0i4πd1(cosα+cosα)
=μ0i4π.3d×2×45=2μ0i15πd
B2=μ0i4πd2(cosβ+cosβ)
=μ0i4π.4d×2×35=3μ0i40πd
BP=2(B1+B2)=2(2μ0i15πd+3μ0i40πd)
=2μ0iπd(215+340=16+9120)
=5μ0i12πd,⊗
(f) 
Magnetic field at P
Due to AB:
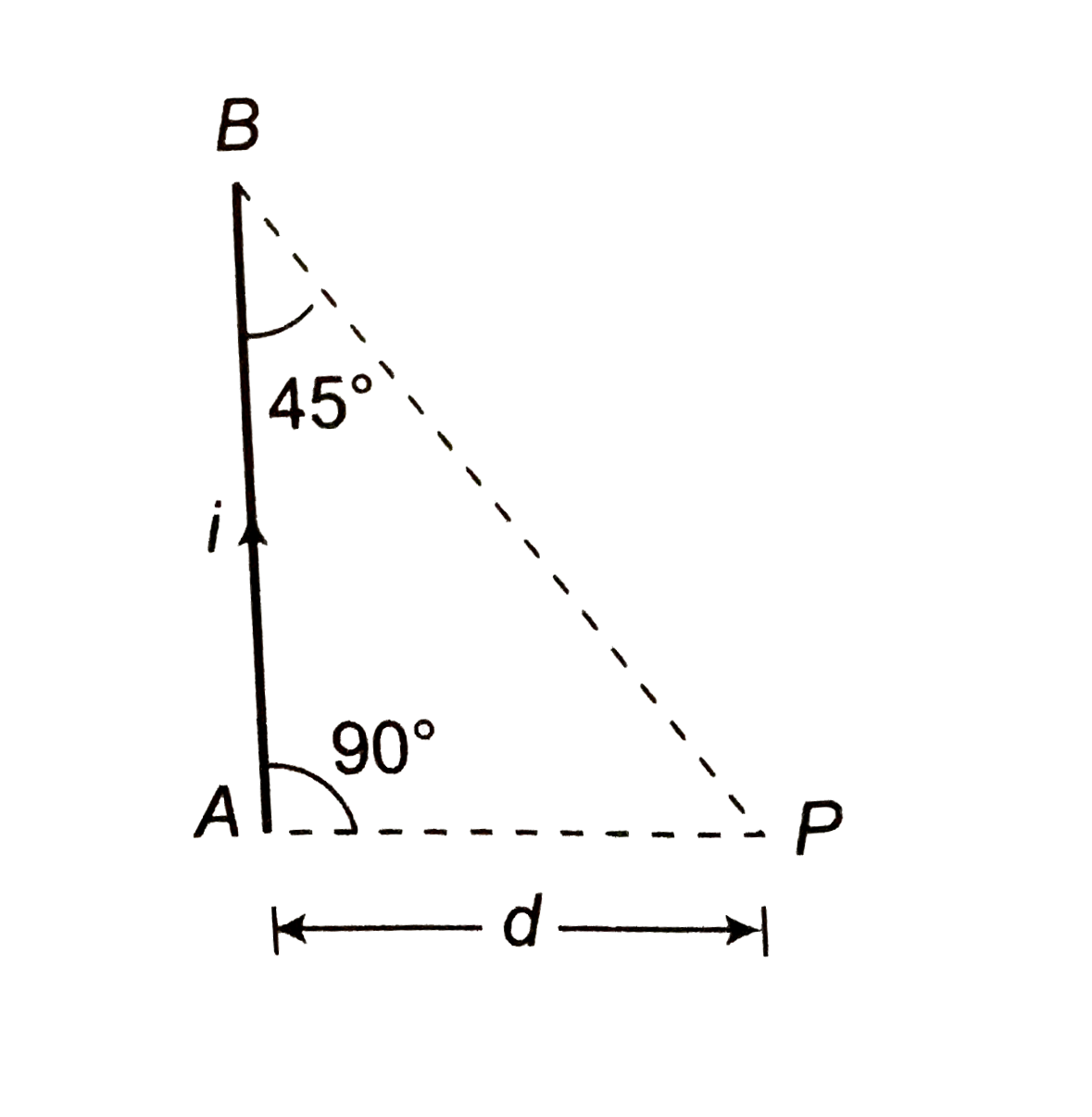
B1=μ0i4πd2(cos90∘+cos45∘)
=μ0i4√2πd,⊗
Due to BC

B2=μ0i4πd2(cos45∘+cos90∘)
=μ0i4√2πd,⊗
Due to CA
B3=μ0i4πd'(cos45∘+cos45∘)
=μ0i4π.d√2×2×1√2=μ0i2πd,⊙
B3>(B1+B2)
BP=B3−(B1+B2)
=μ0i2πd−μ0i2√2πd=μ0i4πd(2−√2),⊙
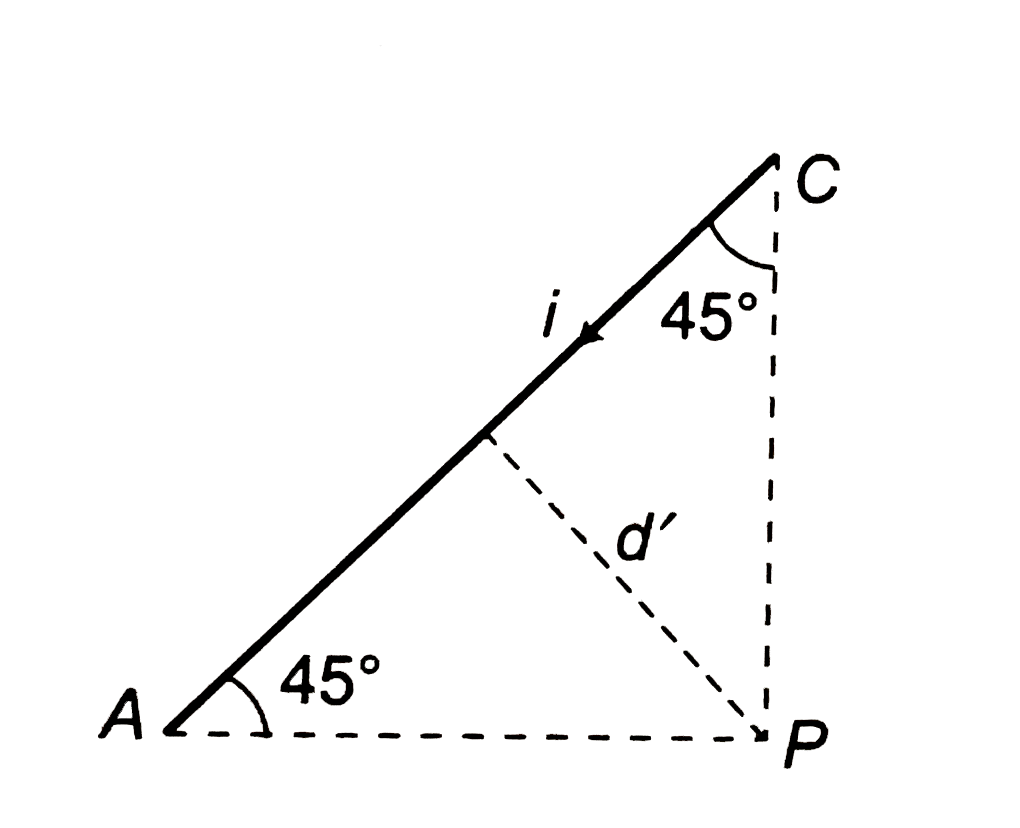
(g) 
d'=dsin.θ2
B1=μ0i4πd'(cos.θ2+cos0)
=μ0i4πdsin.θ2(1+cos.θ2)
=μ0i4πd(2sin.θ4cos.θ4)(1+2cos2.θ4−1)
=μ0i4πdcot.θ4=B2,⊙
BP=B1+B2=2B1
=μ0i2πdcot.θ4,⊙
(h) 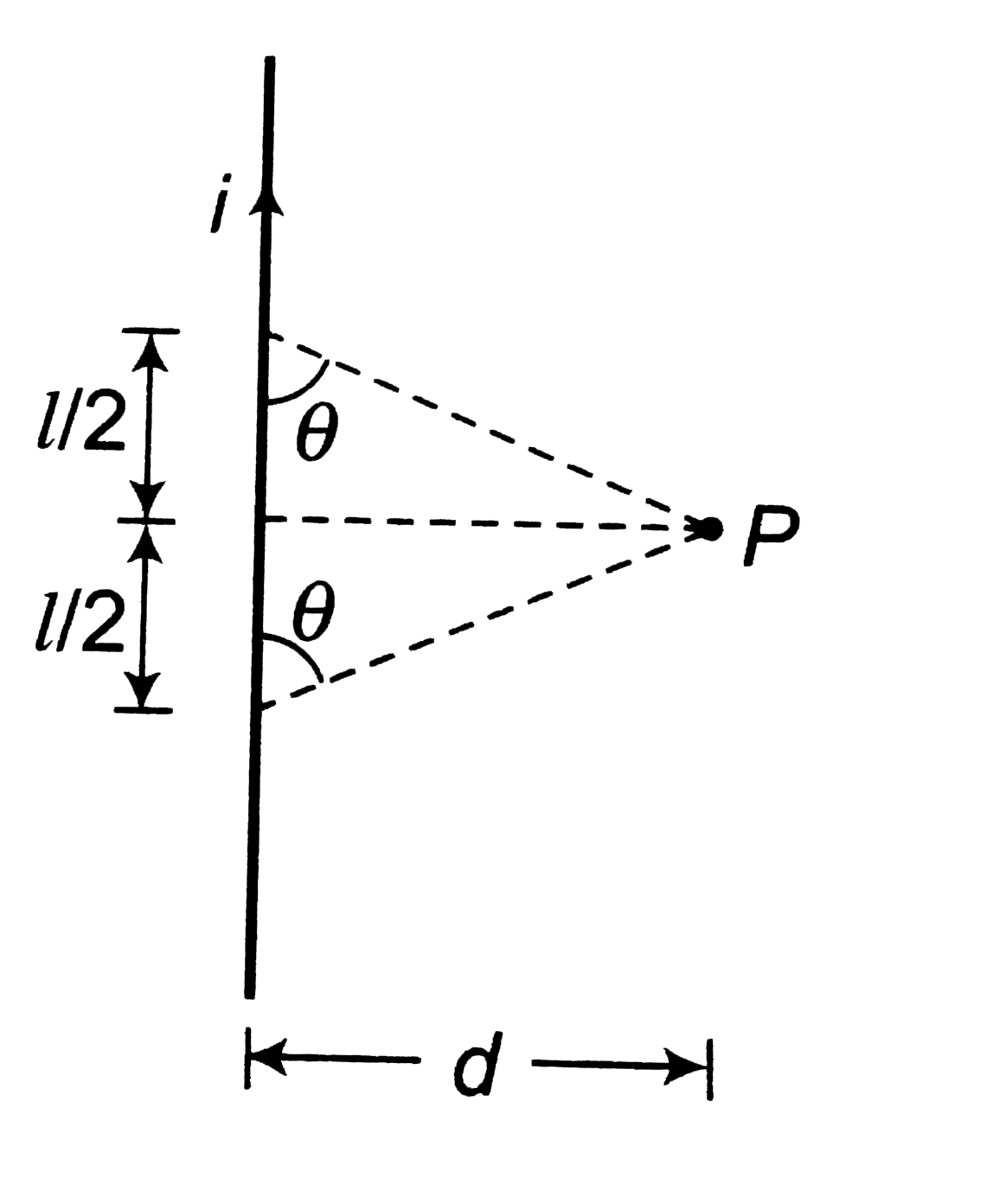
B1=μ0i2πd
B2=μ0i4πd(cosθ+cosθ)
cosθ=l/2√(l/2)2+d2=l√l2+4d2
B1>B2
B1−B2=1100B1
99100B1=B2
99100×μ0i2πd=μ0i4πd×2×l√l2+4d2
(99)√l2+4d2=100l
(99)2(l2+4d2)=(1002)l2
(99)24d2=(1002−992)l2
d2l2=(199)(1)(99)2×4
dl=0.07
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The magnetic field at centre , P will be
 Aμ04πBμ0πCμ02πD4μ0π
Aμ04πBμ0πCμ02πD4μ0πThe magnetic field at the point O in the following current carrying square loop at the centre will be
 A12×10−5 TB4×10−5 TC4√2×10−5 TD2√2×10−5 T
A12×10−5 TB4×10−5 TC4√2×10−5 TD2√2×10−5 TA long, straight wire carries a current i. The magnetizing field intensity H is measured at a point P close to the wire. A long, cylindrical iron rod is brought close to the wire so that the point P is at the centre of the rod. The value of H at P will
Aincrease many timesBdecrease many timesCremain almost constantDbecome zero
Find the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

View SolutionFind the magnetic field B at the centre of a rectangular loop of length l and width b, carrying a current i.
View SolutionFind the magnetic field B at the centre of a rectangular loop of length l and width b, carrying a current i.
View SolutionA long, straight wire carries a current i. The magnetizing field intensity H is measured at a point P close to the wire. A long, cylindrical iron rod is brought close to the wire so that the point P is at the centre of the rod. The value of H at P will
View Solution