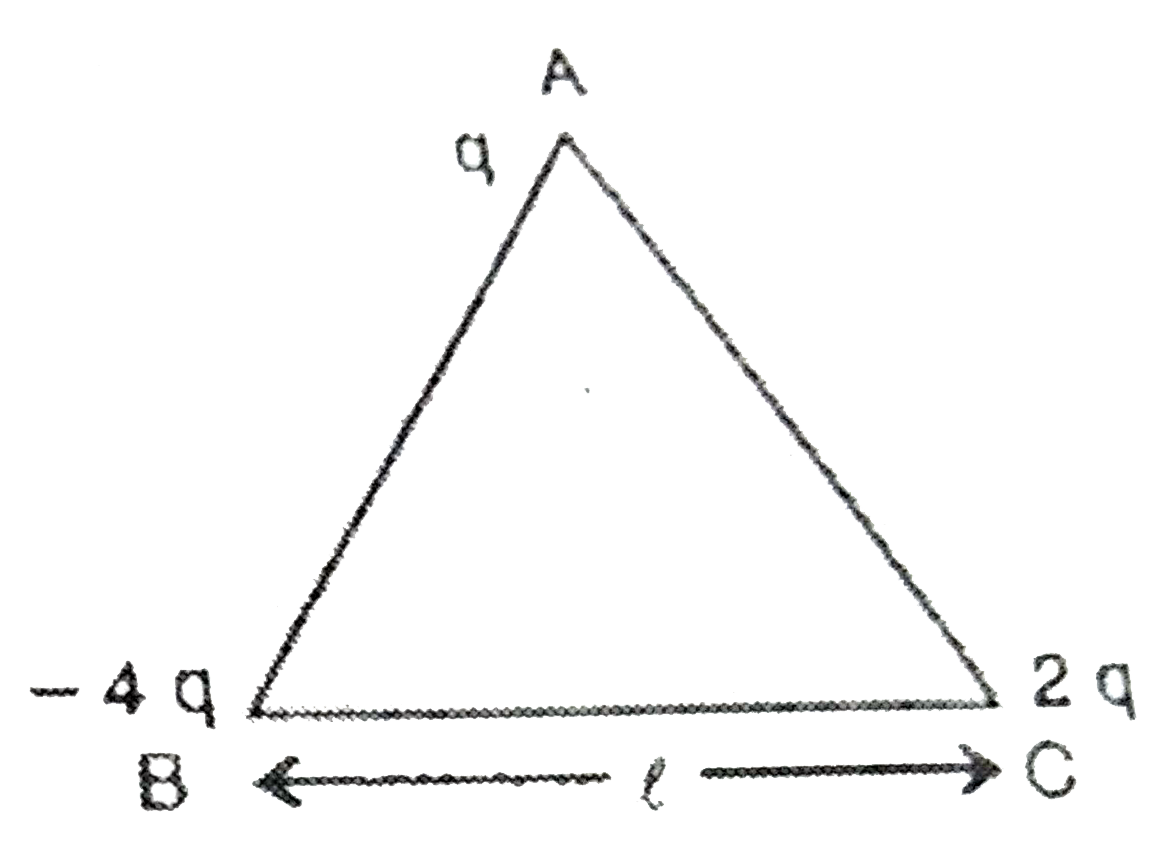
Find out the amount of the work done to separate the charges at infinite distance .
Potential energy of charge system.
U=14π∈0[qAqBAB+qAqBAC+qBqCBC]=14π∈0[q(−4q)l+q(2q)l+(−4q)(2q)l]
=−14π∈0⋅10q2l
∴ Work done to separate the charges at infinite distance
W=U∞+U=+14π∈0⋅10q2l
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - LONG ANSWER QUESTIONS-II
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SELF ASSESSMENT TEST
1 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SHORT ANSWER QUESTIONS
48 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D
1 Videos
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
6 Videos
Similar Questions
(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work 4one to separate the charges at infinite distance.
View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work 4one to separate the charges at infinite distance.

View SolutionFind out the amount of the work done to separate the charges at infinite distance.
View SolutionCharges +q and −q are located at the corners of a cube of side as show in the figure. Find the work done to separate the charges to infinite distance
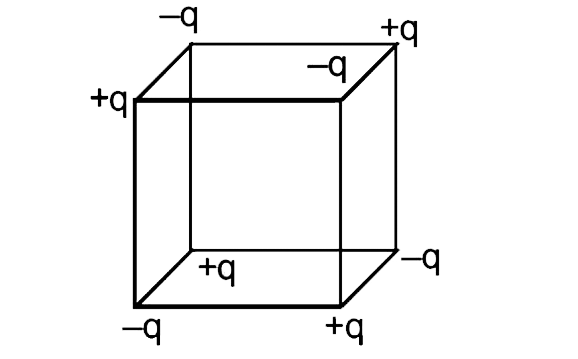
View SolutionCharges +q and −q are located at the corners of a cube of side as show in the figure. Find the work done to separate the charges to infinite distance

View SolutionTwo point charges 9 μC and −2μC are placed at a separation of 20 cm from each other.
(i) Calculate the electric potential energy of this system of two charges.
(ii) What amount of work is required to separate the particles to infinite separation?
View Solution(a) Use Gauss's theorem to find the electric field due to a uniformly charged infinitely
Iarge plane thin sheet with surface charge density.Σ
(b) An infinitely large thin plane sheet has a uniform surface charge density +σ. Obtain the
expression for the amount of work done in bringing a point charge q from infinity to a
point , distant r, in front of the charged plane sheet.
View Solution(a) Use Gauss's theorem to find the electric field due to a uniformly charged infinitely
Iarge plane thin sheet with surface charge density.Σ
(b) An infinitely large thin plane sheet has a uniform surface charge density +σ. Obtain the
expression for the amount of work done in bringing a point charge q from infinity to a
point , distant r, in front of the charged plane sheet.
View Solution(a). Determine the potential energy of a system containing two charges 7μC and −2μC separated by a distance 18 cm. (b) How much work is needed to separate the two charges infinitely away from each other?
View SolutionWhat is meant by equipotential surface? Show that the amount of work done in moving a test positive charge along the equipotential surface is zero.
View Solution
