Find an expression for the potential at a point due to a point charge Q.
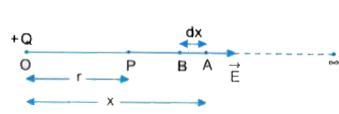
Consider a charge + Q situated at point O and let us want to determine electric potential due to it at a point P situated at a distance r. Then, by definition potential is equal to amount of work done in order to bring unit +ve charge, without any acceleration, from ∞ to point P.
∴V=W∞−p=r∫∞→E.−→dx=−r∫∞Edx=−r∫∞Q4πε0x2dx
=Q4πε0[1x]r∞=Q4πε0[1r−1∞]=Q4πε0r
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - LONG ANSWER QUESTIONS-I
64 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - LONG ANSWER QUESTIONS-II
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - VERY SHORT ANSWER QUESTIONS
40 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D
1 Video
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
6 Videos
Similar Questions
Value of potential at a point due to a point charge is
View SolutionExplain the physical meaning of potential and potential difference. Find a relation for electrostic potential at a point due to a point charge.
View SolutionObtain an expression for electric potential .V due to a point charge .Q at a distance r.
View SolutionWrite an expression for potential at a point P −→(r) due to two point charges q1andq2 at →r1and→r2 respectivley.
View Solution(a) Obtain the expression for the potential due to a point charge.
(b) Use the above expression to show that the potential, due to an electric dipole (length 2a), varies as the inverse square' of the distance r of the 'field point' from the centre of the dipole for r>a.
View Solution(a) Obtain the expression for the potential due to a point charge.
(b) Use the above expression to show that the potential, due to an electric dipole (length 2a), varies as the inverse square' of the distance r of the 'field point' from the centre of the dipole for r>a.
View SolutionDerive an expression for electric field intensity at a point due to point charge.
View SolutionDerive an expression for electric field intensity at a point due to point charge.
View SolutionApply Gauss's theorem to find an expression for the electric field intensity at a point due to a point charge.
View SolutionDeduce an expression for the electric potential due to an electric dipole at any point on its axis. Mention one contrasting feature of electric potential at a point due to dipole as compared to that due to a single charge.
View Solution
