Find out the units and dimensions of the constants a and b in the vander waal.s equation (P+aV2)(V−b)=RT.
We can add and subtract only like quantities.
⇒ Dimensions of P = Dimensions of aV2 ...(i)
and Dimensions of v = Dimensions of b ….(ii)
From (i),
Dimensions of a = Dimensions of P× Dimensions of V2
[a]=[M1L−1T−2]×[L3]2=[M1L5T−2]
Unit of a = Unit of p× Unit of v2=NM2×m6=Nm4
From (ii) , [b]=[V]=M0L3T0]
So unit of b = Unit of V=m3
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Exercise 1.1
16 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Exercise 1.2
6 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Knowledge Check
In the Van der Waals equation (P+aV2)(V−b) = constant, the unit of a is
Adyne/cm5Bdyne/cm4Cdyne/cm3Ddyne/cm2The van der Waal equation of gas is
(P+n2aV2)(V−nb)=nRTA(i) CO2 , (ii) H2B(i) CH4 , (ii) CO2C(i) H2 , (ii) CO2DO2, (ii) H2
The units of constant b used in van der Waals' equation are ………….. .
View SolutionWrite the units of van der Waals' constant 'a' and 'b'.
View SolutionThe ratio of units of van der Waals constants a and b is
View SolutionFor real gases, the relation between P, V and T is given by an van der Waals equation, (P+an2V2)(V−nb)=nRT.
For the following gases CH4,CO2,O2,H2 which gas will have (i) highest value of 'a' and (ii) lowest value of 'b' respectively?
View SolutionThe ratio a/b (the terms used in van der Waals' equation) has the unit .
View SolutionAt a particular temperature and pressure for a real gas Van der Waal's equation can be written as:
(P+aV2m)(Vm−b)=RT
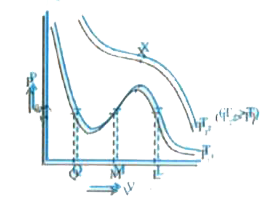
where Vm is molar volume of gas. This is cubic equation in the variable Vm and therefore for any single value of P & T there should be 3 values of Vm. Which are shown in graph as Q, M and L.
As temperature is made to increase at a certain higher temperature the three values of Vm becomes identical. The temperature, pressure & molar volume at point X are called Tc, Pc & Vc for real gas. The compressibility factor in terms of Pc, Vc and T is called Zc.
The expression of Van dcr Waal's constant 'a' can be given as
View Solution
