Doubtnut Promotions Sticky

At a particular temperature and pressure for a real gas Van der Waal's equation can be written as:
(P+aV2m)(Vm−b)=RT
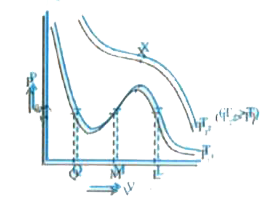
At a particular temperature and pressure for a real gas Van der Waal's equation can be written as: (P + a/(V^(2)m)) (V(m) -b) =RT where Vm is molar volume of gas. This is cubic equation in the variable Vm and therefore for any single value of P & T there should be 3 values of Vm. Which are shown in graph as Q, M and L. As temperature is made to increase at a certain higher temperature the three values of Vm becomes identical. The temperature, pressure & molar volume at point X are called Tc, Pc & Vc for real gas. The compressibility factor in terms of Pc, Vc and T is called Zc. The expression of Van dcr Waal's constant 'a' can be given as
where Vm is molar volume of gas. This is cubic equation in the variable Vm and therefore for any single value of P & T there should be 3 values of Vm. Which are shown in graph as Q, M and L.
As temperature is made to increase at a certain higher temperature the three values of Vm becomes identical. The temperature, pressure & molar volume at point X are called Tc, Pc & Vc for real gas. The compressibility factor in terms of Pc, Vc and T is called Zc.
The expression of Van dcr Waal's constant 'a' can be given as

A

27RTc16Pc

B

27(RTc)264Pc

C

64(RTc)2Pc

D

27Pc(RTc)2

Video Solution
Doubtnut Promotions Banner
|
Answer

Step by step video & image solution for At a particular temperature and pressure for a real gas Van der Waal's equation can be written as: (P + a/(V^(2)m)) (V_(m) -b) =RT where Vm is molar volume of gas. This is cubic equation in the variable Vm and therefore for any single value of P & T there should be 3 values of Vm. Which are shown in graph as Q, M and L. As temperature is made to increase at a certain higher temperature the three values of Vm becomes identical. The temperature, pressure & molar volume at point X are called Tc, Pc & Vc for real gas. The compressibility factor in terms of Pc, Vc and T is called Zc. The expression of Van dcr Waal's constant 'a' can be given as by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.