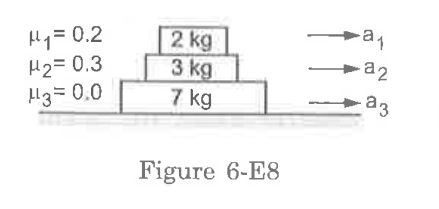
Find the acceleration a1,a2anda3 of the three blocks shown in Fig if a horizontal force of 10N is applied on

(a) 2kg blocks, (b) 3kg blocks and ( c) 7kg blocks (Take g=10ms−2)
When force of 10N is applied on 2kg blocks . The limiting friction force between 2kgand3kg blocks
fl1=0.2×2kg=0.2×2×10=4N
The limiting friction force between3kg and 7kg
fl2=0.3×5g
=0.3×5×10=15N
After proper analysis , we find that 2kg will slip over 3kg but 3kg will not slip over 7kg
Thus the we have a1=10−42=3ms−2
a2=a3=43+7=0.4ms−2
Since a1 is coming out to be greater than a2,2kg will slip over 3kg

b. When force of 10N is applied on 3kg blocks
Let us assume that all these blocks move together with common acceleration a then

a=102×3+7=56ms−2
Under this assumption
Friction between 2kg and 3kg
f1=2a=2×56=53N<fl1
Friction between 3kg and 7kg
f2=7a=(7×5)(6)353N<fl2
Hence, no slipping occut any where
c. When force of 10N is applied on 7kg block. The acceleration of the whole system

a=102×3+7=56ms−2
The pseudo force on 2kg block =2×56=53N ,which is less than the friction forces between 2kg and 3kg blocks so they move together.
Now check whether 2kg and 3kg move together over 7kg blocks The pseudo force on (2+3)kg is 5×56=256N , which is also less than friction force between 3kg and 7kg blocks move with a common acceleration of 5/6ms−2 Therefore
a=a1=a2=a3102+3+7=56ms−2
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.1
25 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.2
16 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Knowledge Check
Three blocks of masses 5 kg, 3 kg and 2 kg are placed on a rough surface as shown in figure. Coefficient of friction between block and surface is same for all the blocks and is equal to μ=0.2 . A horizontal force of 15 N is applied on 5 kg block. The force exerted by 3 kg block on 2 kg block is : (g = 10 m/s2)
 A15 NB5 NCzeroDNone of these
A15 NB5 NCzeroDNone of theseA 3 kg block is placed over a 10 kg block and both are palced on a smooth horizontal surface. The coefficient of friction between the block is 0.2 . If a horizontal force of 20 N is applied to 3 kg block, accelerations of the two block in ms−2 are (take, g=10ms−2)
 A134,0.6B144,3C134,3D143,0.6
A134,0.6B144,3C134,3D143,0.6Consider the arrangement shown in the figure. The coefficient of friction between the two blocks is 0.5 and between the 4 kg block and the horizontal surface is 0.4. If a horizontal force of 12 N is applied on the 4 kg block, the acceleration of the 2 kg block would be
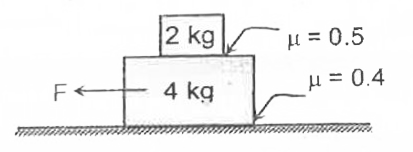 A2.5m/s2B2m/s2C5m/s2Dzero
A2.5m/s2B2m/s2C5m/s2Dzero
Three blocks of masses 3kg,2kg and 1kg are placed side by side on a smooth surface as shown in figure. A horizontal force of 12N is applied on 3kg block. Find the net force on 2kg block.

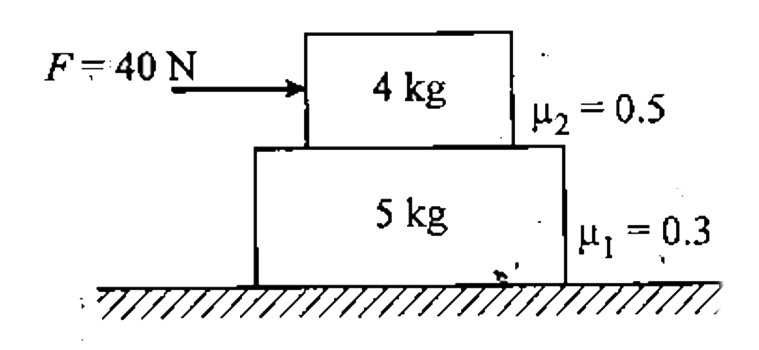
View SolutionFind the acceleration of the two blocks of 4 kg and 5 kg mass if a force of 40 N is applied on 4 kg block. Friction coefficients between the respective surface are shown in figure-2.92. Take g=10m/s2
View SolutionA block of mass 50 kg is kept on another block of mass 1 kg as shown in figure. A horizontal force of 10 N is applied on the 50kg block. (All surface are smooth). Find
(g=10m/s2)
Force exerted by B on A.
View SolutionA horizontal force of 4 N is applied to a block of mass 2 kg resting on a frictionless table. What is the acceleration of the block in ms−2 ?
View SolutionTwo blocks A and B of masses 10 kg and 15 kg are placed in contact with each other rest on a rough horizontal surface as shown in the figure. The coefficient of friction between the blocks and surface is 0.2. A horizontal force of 200 N is applied to block A. The acceleration of the system is (Take g=10ms−2)
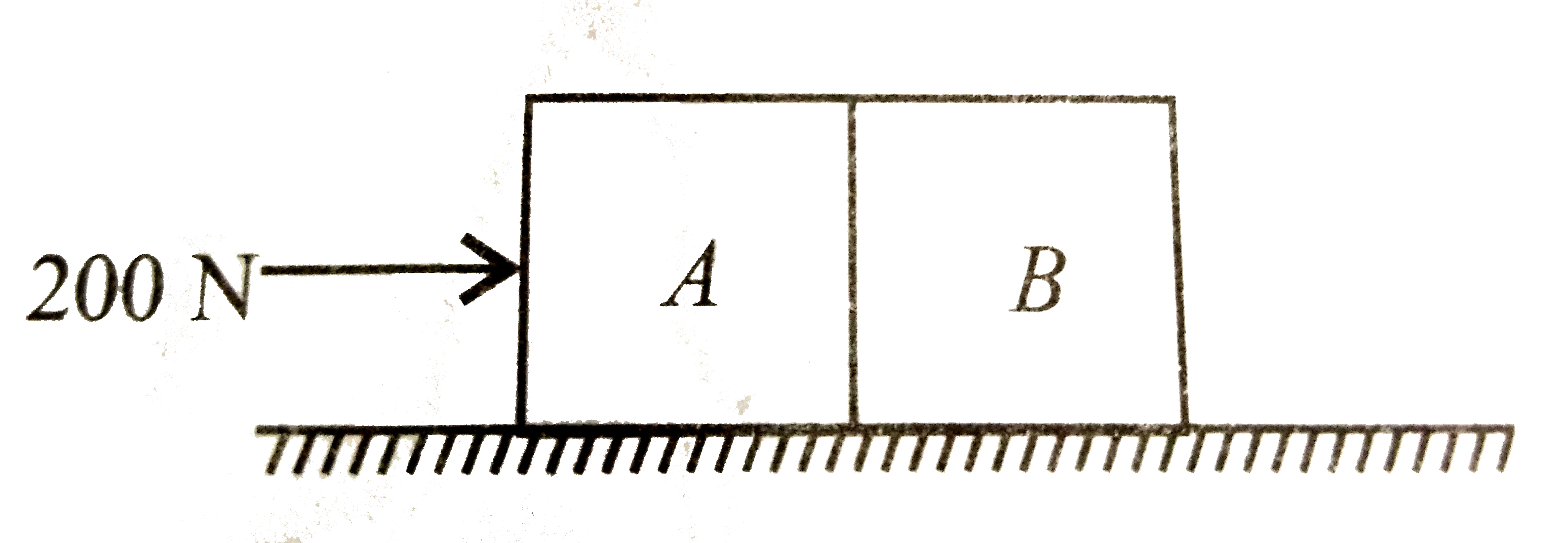
View Solution