Find the aperture angle of a cone in which all the stars located in the semi-sphere for a observer on the Earth will be visible if one moves relative to the Earth with relativistic velocity V differing by 1.0% from the velocity of light. Make use of the formula of the foregoing problem.
The statement of the problem is not quite properly worked and is in fact misleading. The correct situation is described below. We consider for simplicity, stars in the x−z plane. Then the previous formula is applicable, and we have
cosθ'=cosθ−β1−βcosθ=cosθ−0.991−0.9cosθ
The distribution of θ' is given in the diagram below
The light that appears to come from the forward quadrant in the frame K(θ=−π to θ=−π/2) is compressend into an angle of magnitude +81∘ in the forward direction while the remaining stars are spread out.
The three dimensional distribution can also be found out from the three dimensional generalization of the formula in the previous problems.
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Thermal Equation47videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise2videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Dispersion And Absorption Of Light24videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems92videos
MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
Similar Questions
A rocket moves in the absence of external forces by ejecting a steady jet with velocity u constant relative to the rocket. Find the velocity v of the rocket at the moment when its mass is equal to m, if at the initial moment it possessed the mass m0 and its velocity was equal to zero. Make use of the formula given in the foregoing problem.
View SolutionAn imaginary space rocket launched from the Earth moves with an acceleration w′=10g which is the same in every instantaneous co-moving inertial reference frame. The boost stage lasted τ=1.0 year of terrestrial time. Find how much (in per cent) does the rocket velocity differ from the velocity of light at the end of the boost stage. What distance does the rocket cover by that moment?
View Solution
Knowledge Check
- Question 1 - Select One
The wavelength of light observed on the earth, from a moving star is found to decrease by 0.05%. Relative to the earth the star is
AMoving away with a velocity of 1.5×105m/sBComing closer with a velocity of 1.5×105m/sCMoving away with a velocity of 1.5×104m/sDComing closer with a velocity of 1.5×104m/s - Question 2 - Select One
The wavelength of light observed on the earth , from a moving star is found to decrease by 0.05% .Relative to earth , the star is
Amoving away with a velocity of 1.5×105m/sBcoming closer with a velocity of 1.5×105m/sCmoving away with a velocity of 1.5×104m/sDcoming closer with a velocity of 1.5×104m/s - Question 3 - Select One
The apparent wavelength of light from a star moving away from the earth is 0.02% more than the actual wave length. What is the velocity of star
A30Kms−1B60Kms−1C90Kms−1Dnone of these
The apparent wavelength of light from a star moving away from the earth is 0.02% more than the actual wave length. What is the velocity of star
View SolutionAn asteroid was fast approaching the earth. Scientists fired a rocket which hit the asteroid at a distance of 5 R from the centre of the earth (R = radius of the earth). mmediately after the hit the asteroid’s velocity (V0) was making an angle of θ=30∘ with the line joining the centre of the earth to the asteroid. The asteroid just grazed past the surface of the earth. Find V0 [Mass of the earth = M]
View SolutionThe vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jormalism greatly simplifies many problems. If →vAis the absolute velocity of a body A and →–––(B)that of another body B then the relative velocity of A in relation to B is →–––(AD)=→VA−→vB and →vBA=→vB-→vA.
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A train A moves to the east with velocity of 40 km/hr and a train B moves due north with velocity of 30 km/hr. The relative velocity of A w.rt. B is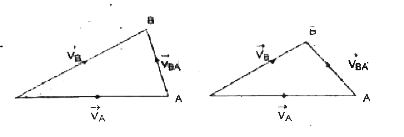
View SolutionThe apparent wavelength of light from a star moving away from earth is observed to be 0.01% more than its real wavelength. The velocity of star is
View SolutionThe vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jormalism greatly simplifies many problems. If →vAis the absolute velocity of a body A and →–––(B)that of another body B then the relative velocity of A in relation to B is →–––(AD)=→VA−→vB and →vBA=→vB-→vA.
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A train A moves to the east with velocity of 40 km/hr and a train B moves due north with velocity of 30 km/hr. The relative velocity of A w.rt. B isView Solution