A rocket moves in the absence of external forces by ejecting a steady jet with velocity u constant relative to the rocket. Find the velocity v of the rocket at the moment when its mass is equal to m, if at the initial moment it possessed the mass m0 and its velocity was equal to zero. Make use of the formula given in the foregoing problem.
According to the question, →F=0 and μ=−dm/dt so the equation for this system becomes,
md→vdt=dmdt→u
As d→v↑↓→u so, mdv=−udm.
Integrating within the limits:
1uv∫0dv=−m∫m0dmm or vu=1nm0m
Thus, v=u1nm0m
As d→v↑↓→u, so in vector form →v=−→u1nm0m
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation
34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body
56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - The Fundamental Equation Of Dynamics
59 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
A relativistic rocket emits a gas jet with non-relativistic velocity u constant relative to the rocket. Find how the velocity v of the rocket depends on its rest mass m if the initial rest mass of the rocket equals to m0.
View SolutionA cart loaded with sand moves along a horizontal plane due to a constant force F coinciding in direction with the cart's velocity vector. In the process, sand spills through a hole in the bottom with a constant velocity μkg/s. Find the acceleration and the velocity of the cart at the moment t, if at the initial moment t=0 the cart with loaded sand had the mass m0 and its velocity was equal to zero. The friction is to be neglected.
View Solution
Knowledge Check
If M is mass of rocket, r is rate of ejection of gases and u is velocity of gases with respect to rocket then acceleration of the rocket dv/dt is equal to
AruM−rtBM−rtruCruM+rtDruM
A cart loaded with sand moves along a horizontal plane due to a constant force F coinciding in direction with the cart's velocity vector. In the process, sand spills through a hole in the bottom with a constant rate μkg/s. Find the acceleration and the velocity of the cart at the moment t, if at the initial moment t=0 the cart with loaded sand had the mass m0 and its velocity was equal to zero. The friction is to be neglected.
View SolutionA rocket motor consumes 100 kg of fuel per second exhausting it with a speed of 6×103ms−1 What thrust is exerted on the rocket ? What will be the velocity of the rocket at the instant its mass is reduced to (1/40) of its initial mass ? Take initial velocity of rocket as zero . Neglect gravity .
View SolutionThe figure shows mass m moves with velocity u. Find the velocity of ring at that moment. Ring is restricted to move on smooth rod.
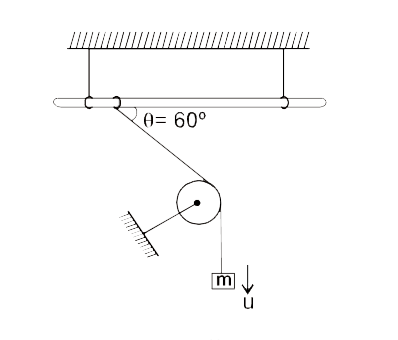
View SolutionA rocket burns 0.5 kg of fuel per second ejecting it as gases with a velocity of 1600m/s relative to the rocket . How much force is exerted on the rocket ? Also , calculate the velocity attainted by the rocket , when its mass
reduces to 1200 th of its initial mass .
View SolutionA rocket of initial mass 6000kg ejects mass at a constant rate of 16kg/s with constant relative speed of 11m/s What is the acceleration of the rocket one mnute after blast ?
View SolutionA rocket motor consumes 100 kg of fuel per second, exhausting it with a speed of 5×103ms−1. (i) What force is exerted on the rocket ? (ii) What will be the velocity of the rocket at the instant its mass is reduced (1/20)th of its initial mass, its initial velocity being zero. Neglect gravity.
View SolutionFind the aperture angle of a cone in which all the stars located in the semi-sphere for a observer on the Earth will be visible if one moves relative to the Earth with relativistic velocity V differing by 1.0% from the velocity of light. Make use of the formula of the foregoing problem.
View Solution
