Find the average velocity for the time intervals Δt=t2−0.75 when t2 is 1.75 ,1.25 and 1.0 s. What is the instantaneous velocity at t=0.75 s?
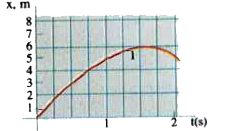
About 2 ms−1,2.7ms−1,3.2ms−1,4.0ms−1 from slope at 0.75 s
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-2)
29 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Question for descriptiv Answers
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - problems
47 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
Similar Questions
A angular positio of a point on the rim of a rotating wheel is given by θ=4t−3t2+t3 where θ is in radiuans and t is in seconds. What are the angualr velocities at
(a).t=2.0 and
(b). t=4.0s
(c). What is the average angular acceleration for the time interval that begins at t=2.0s and ends at t=4.0s?
(d). What are the instantaneous angular acceleration at the biginning and the end of this time interval?
View SolutionThe position of a particle varies with time according to the relation x=3t2+5t3+7t, where x is in m and t is in s. Find
(i) Displacement during time interval t = 1 s to t = 3 s.
(ii) Average velocity during time interval 0 - 5 s.
(iii) Instantaneous velocity at t = 0 and t = 5 s.
(iv) Average acceleration during time interval 0 - 5 s.
(v) Acceleration at t = 0 and t = 5 s.
View SolutionA particle moving with uniform acceleration has average velocities ν1,ν2 and ν3 over the successive intervals of time t1,t2 and t3 respectively. The value of ν1−ν2ν2−ν3 will be
View SolutionA particle executes simple harmonic motion about x=0 along x-axis. The position of the particle at an instant is given by x=(5cm)sinπt. Find the average velocity and average acceleration for a time interval 0−0.5s.
Hint : Average velocity =x2−x1t2−t1
x1=5sin0
x2=5sin(π×0.5)
t2−t1=0.5
Average acceleration =v2−v1t2−t1
v=dxdt=5πcosπt
⇒aav=5πcos(π×0.5)−5πcosθ0.5
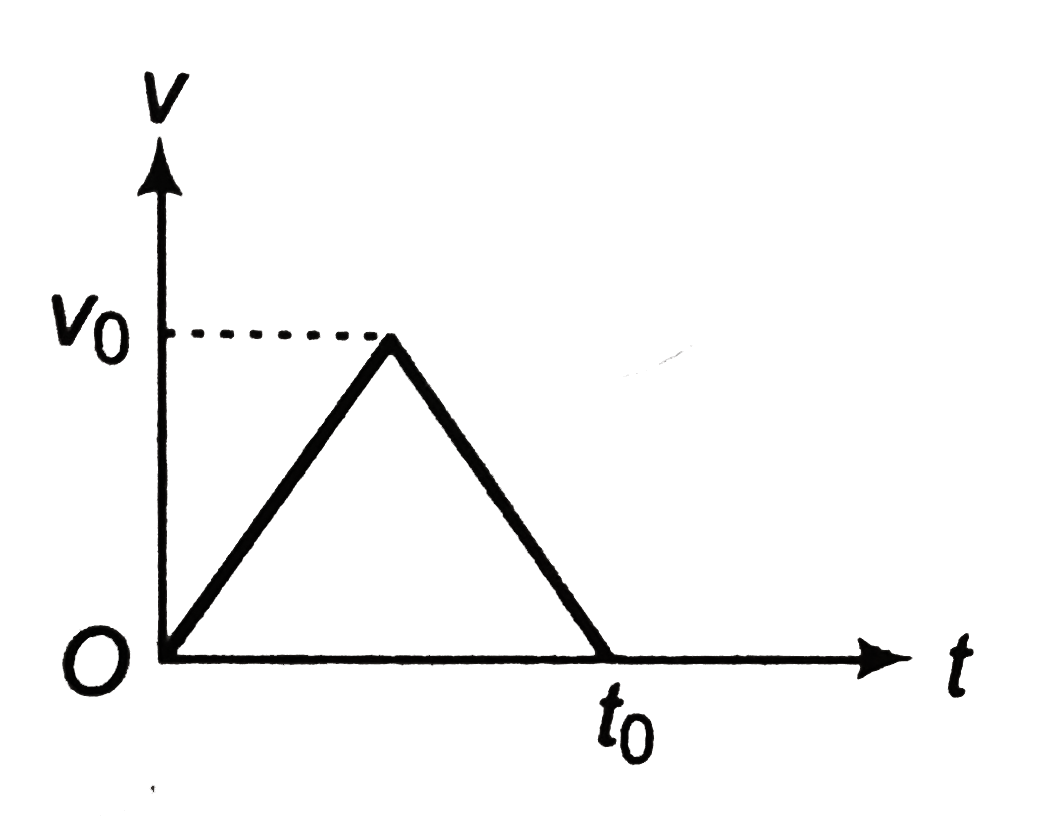
View SolutionAssertion : In v-t graph shown in figure, average velocity in time interval from 0→t0 depends only on v0. It is independent of t0.
Reason : In the given time interval average velocity is v02.
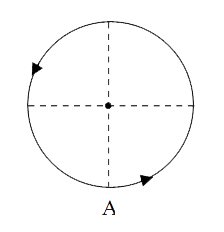
View SolutionA particle is describing uniform circular motion in the anti-clockwise sense such that its time period of revolution is T. At t = 0 the particle is observed to be at A. If θ1 be the angle
between acceleration vector at t=T4 and average velocity vector in the time interval 0 to T/4 and θ2 be the angle between acceleration vector at t=T4 and the vector representing change in velocity in the time interval 0 to T/4, then :
View SolutionThe distance travelled by a particle in time t is given by s=(2.5ms2)t2. Find a. the average speed of the particle during the time 0 to 5.0 s, and b. the instantaneous speed ast t=5.0 is
View SolutionAcceleration of a particle is given by
a=3t2+2t+1
Where t is time . Find
(i) its velocity at time t assuming velocity to be 10 m/s at t = 0.
(ii) its position at time t assuming that the particle is at origin at t = 0.
(iii) What is the average speed of the particle in the duration t = 0 to t = 1s?
(iv) What is the average acceleration of the particle in the duration t = 0 to t = 1s?
View SolutionAssertion : In the υ−t diagram as shown in figure, average velocity between the interval t = 0 and t=t0 is independent of t0
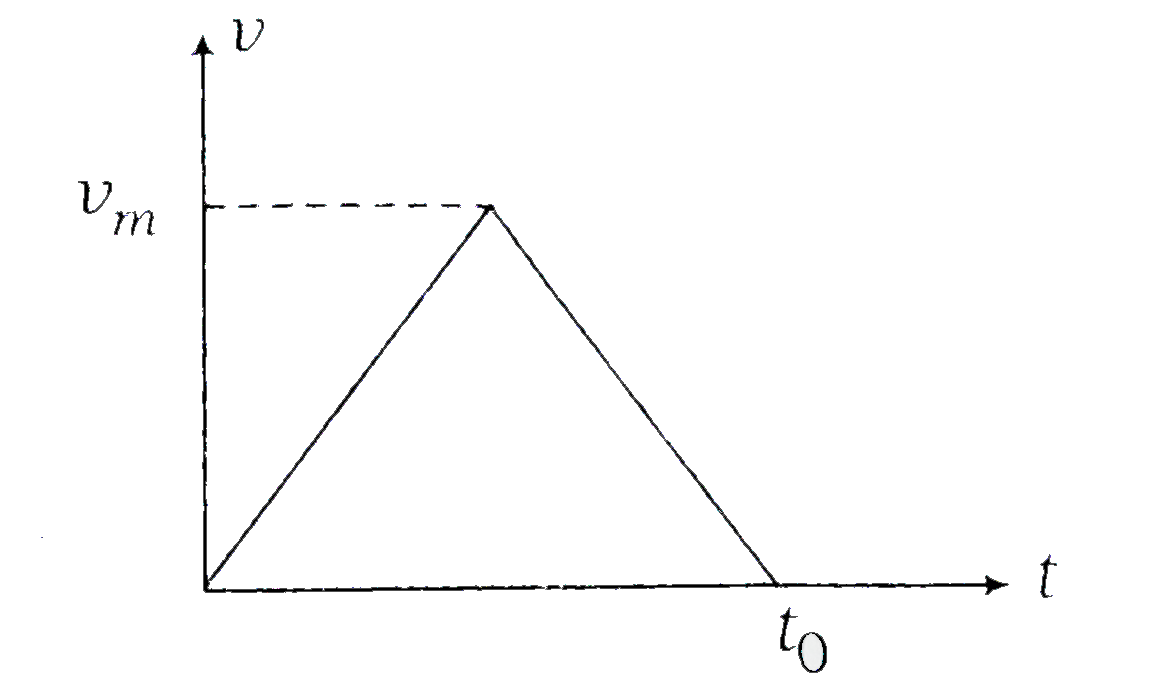
Reason : Average velocity in the given interval is 12υm.
View SolutionThe displacement s of an object is given as a function of time t
s=5t2+9t
Calculate the instantaneous velocity of object at t = 0.
View Solution
