Find the charge on the three capacitors shown in figure.
(a) 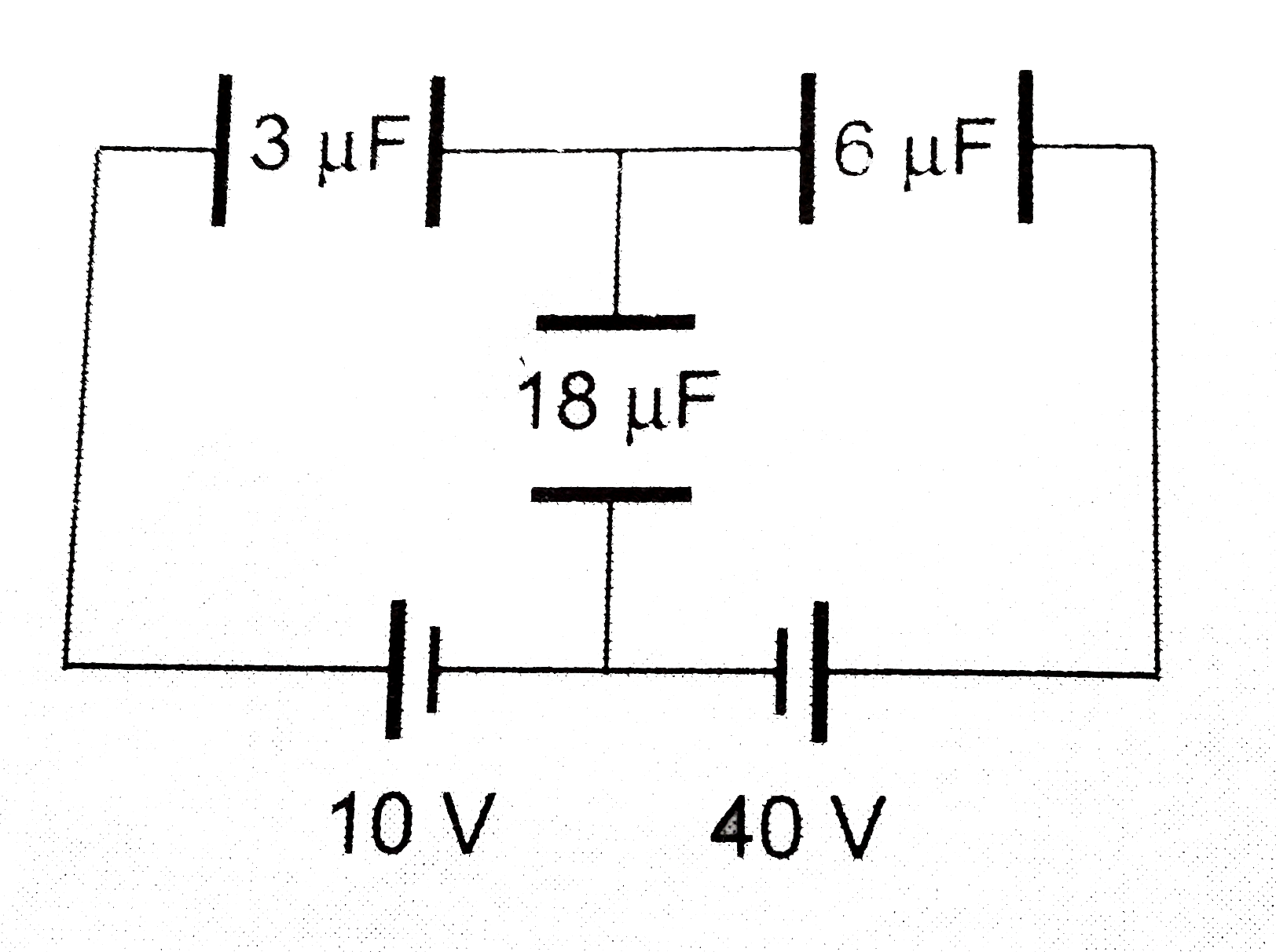
(b) 
Text Solution
(a) 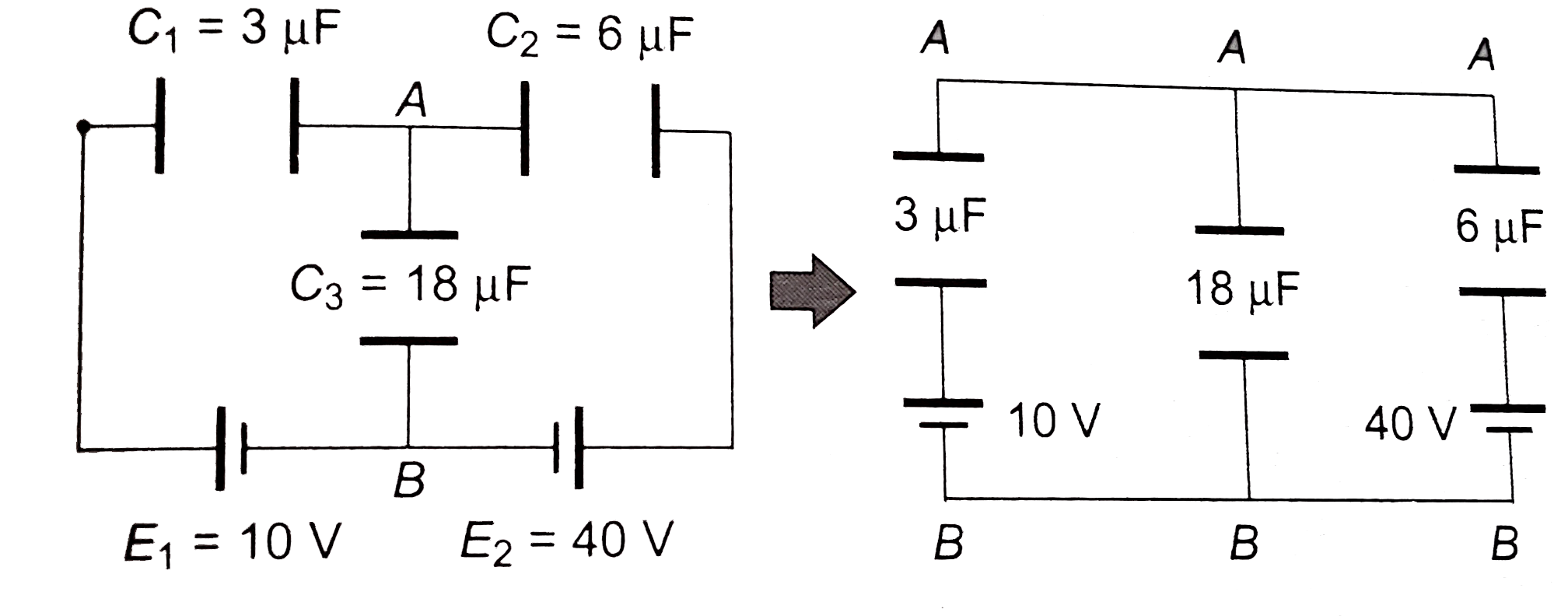
The cells is parallel can be replaced by a single cell.
E=C1E1+C2E2C1+C2=3×10+6×403+6=30+2409=30V
C=C1+C2=3+6=9μF
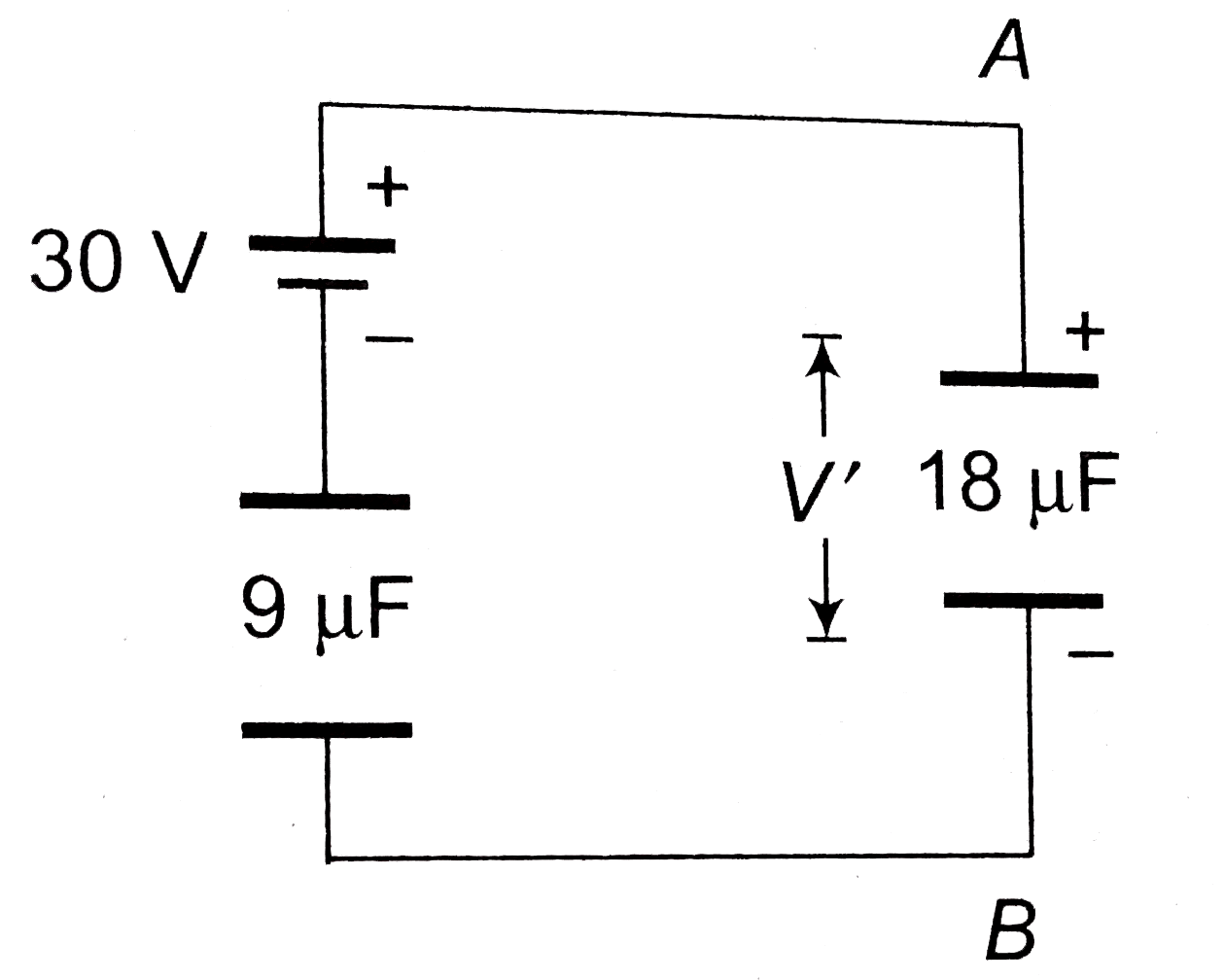
V'=(99+18)×30=10V
VA−VB=10V
Now return to previous diagram :

Branch A×B
VA−Q23−10=VB
VA−VB−10=Q23
10−10=Q23⇒Q2=0
Branch AYB :
VA−Q16−40=VB
VA−VB−40=Q16
10−40=Q16⇒Q1=−180μC
Q1+Q2=−180μC
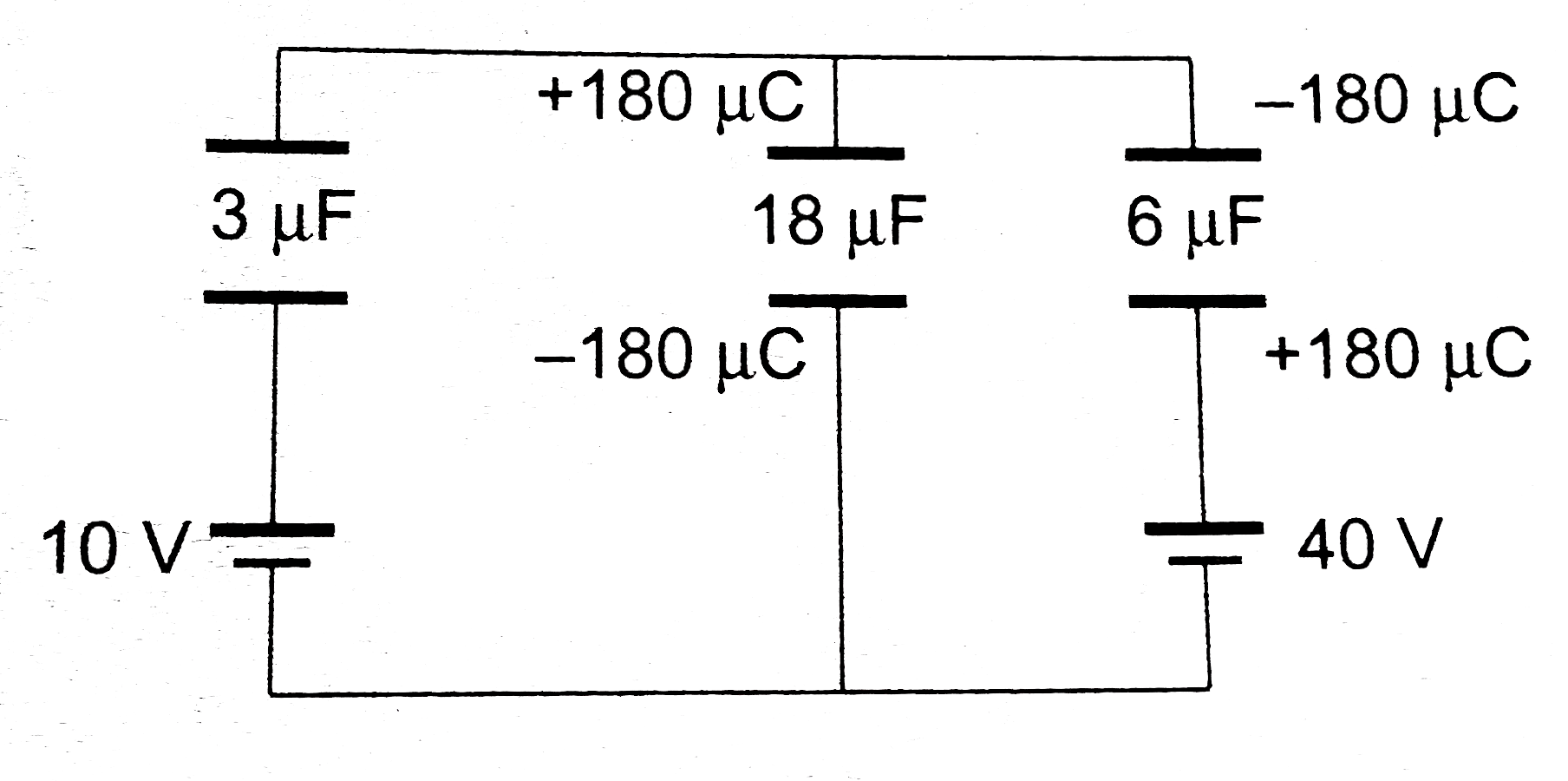
Charge on capacitor
3μF:0,18μF:180μC,6μF:180μC.
Alternatively by Kirchoff's rules
Assume charge in branches, balancing at junctions.
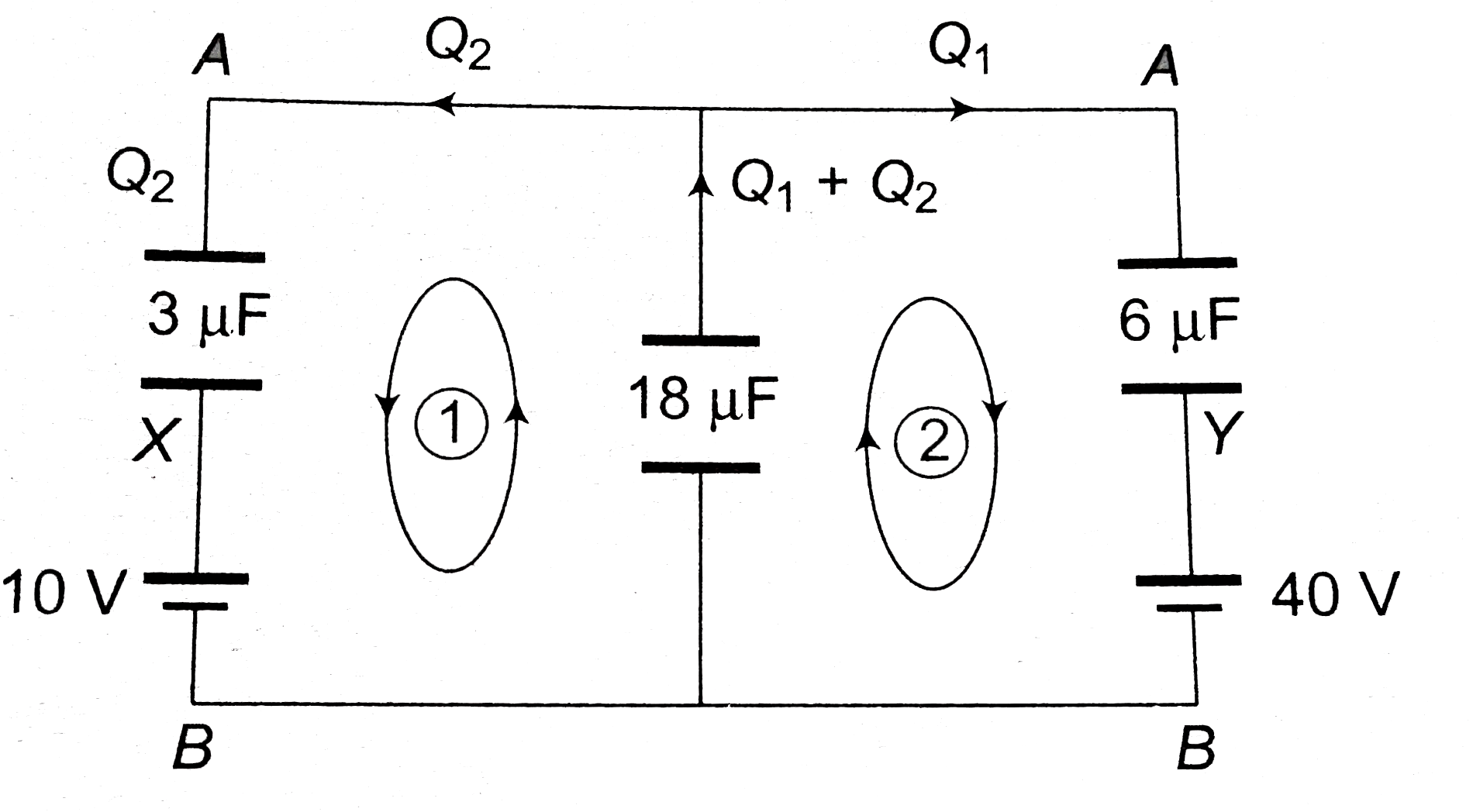
Left loop :
VA−Q23−10−(Q1+Q2)18=VA
−Q1−7Q2=180
Q1+7Q2=−180....(i)
Right loop :
VA−Q16−40−Q1+Q218=VA
4Q1+Q2=−720
Solving (i) and (ii)
Q1=−180μC,Q2=0
(b) 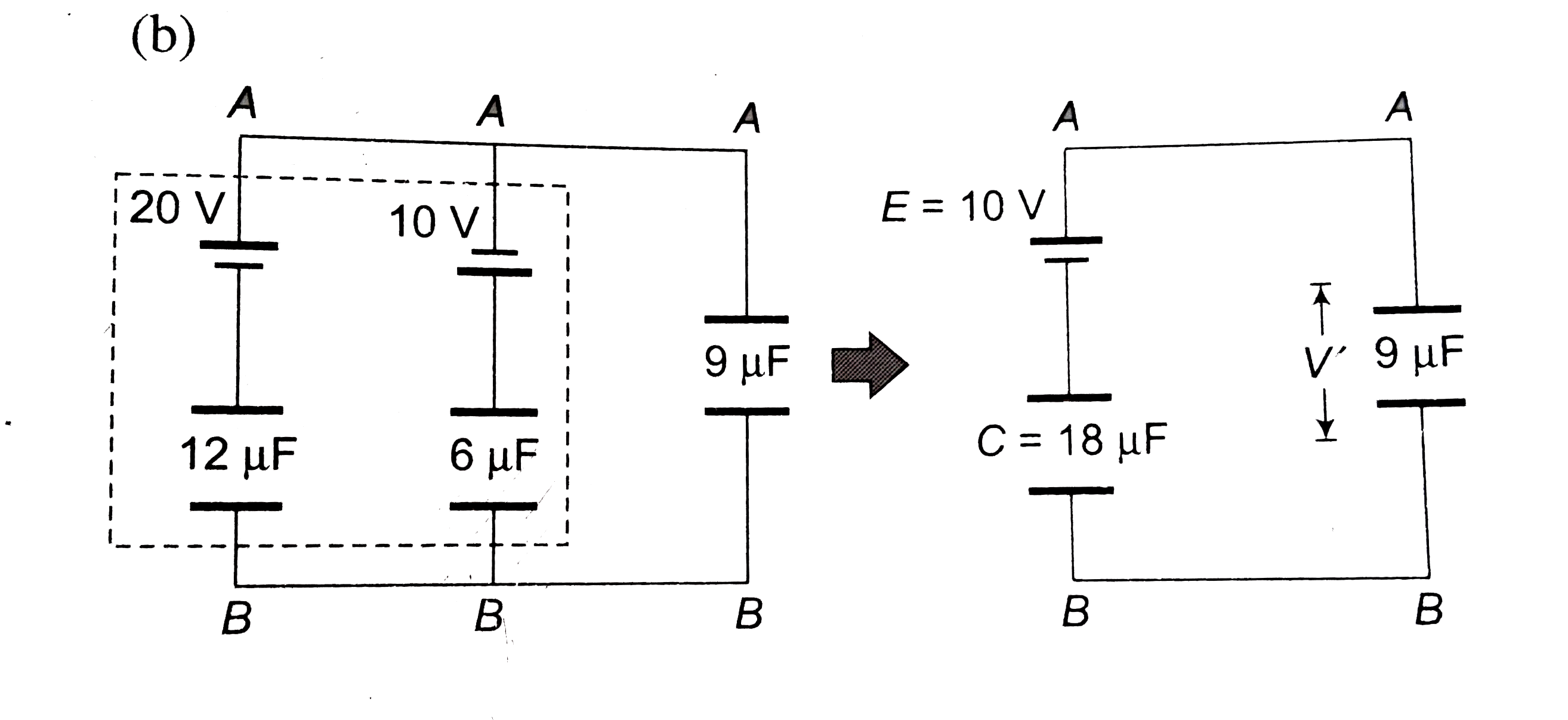
E=20×12−10×612+6=10V
C=12+6=18μF
V'=(8018+9)×10=203V
charge on 9μF:9×203=60μC
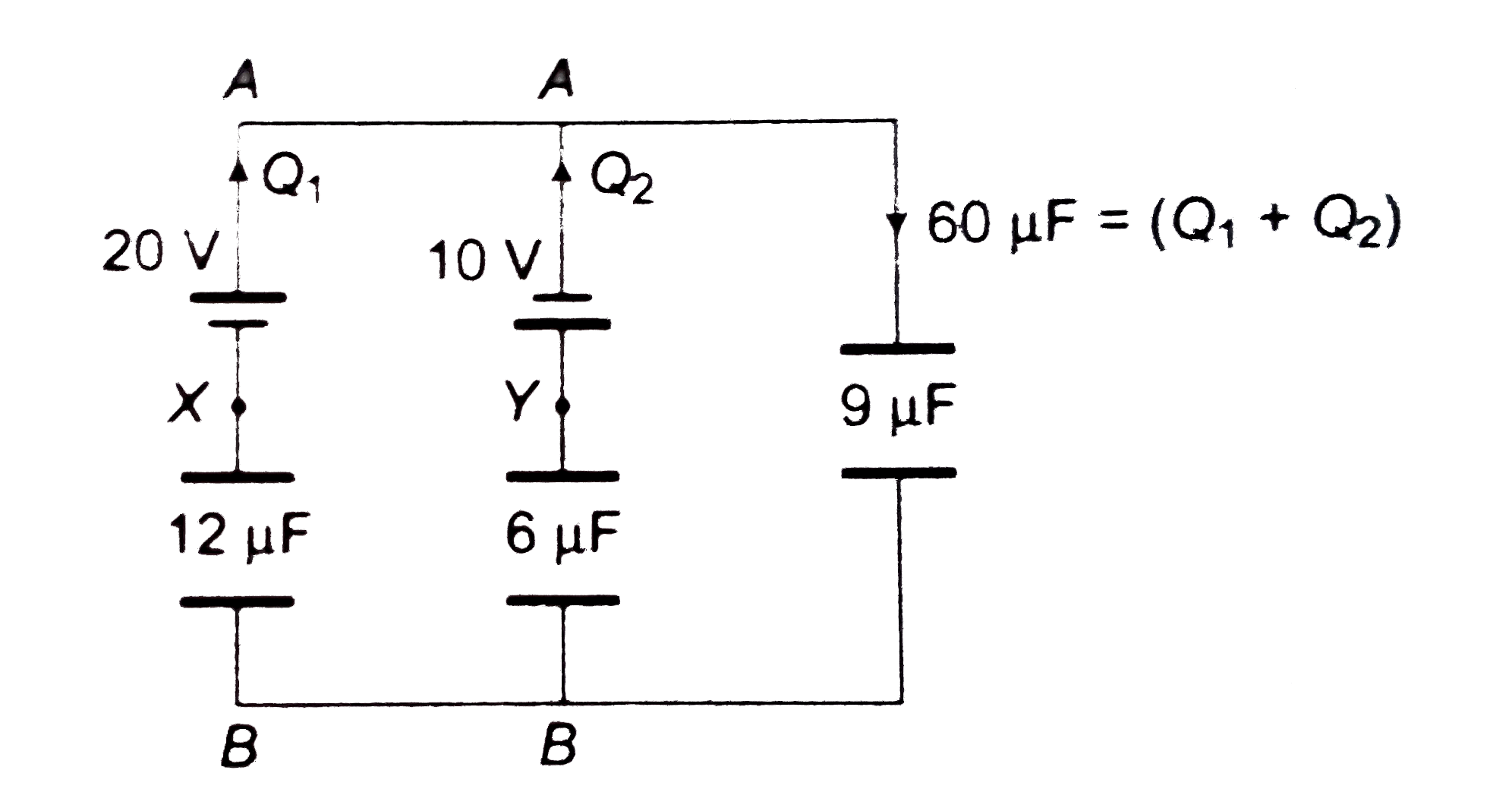
Branch AXB :
VA−20+Q112=VB
Q112=VB−VA+20=−203+20=403
Q1=160μC
Branch AYB :
VA+10+Q16=VB
VA−VB+10=−Q26
203+10=−Q26
Q2=−100μC
Check : Q1+Q2=60μC,O.K.
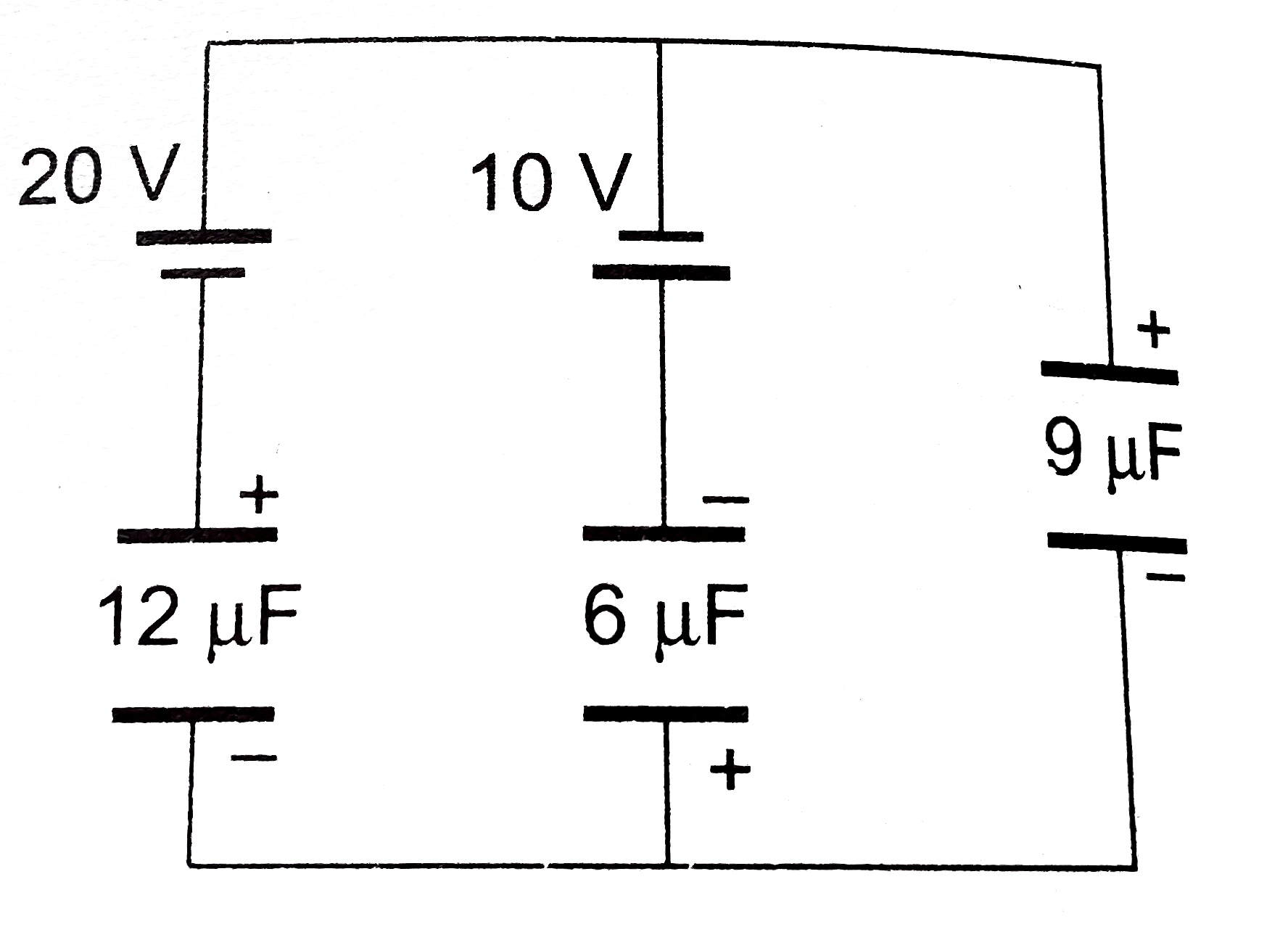
( c) 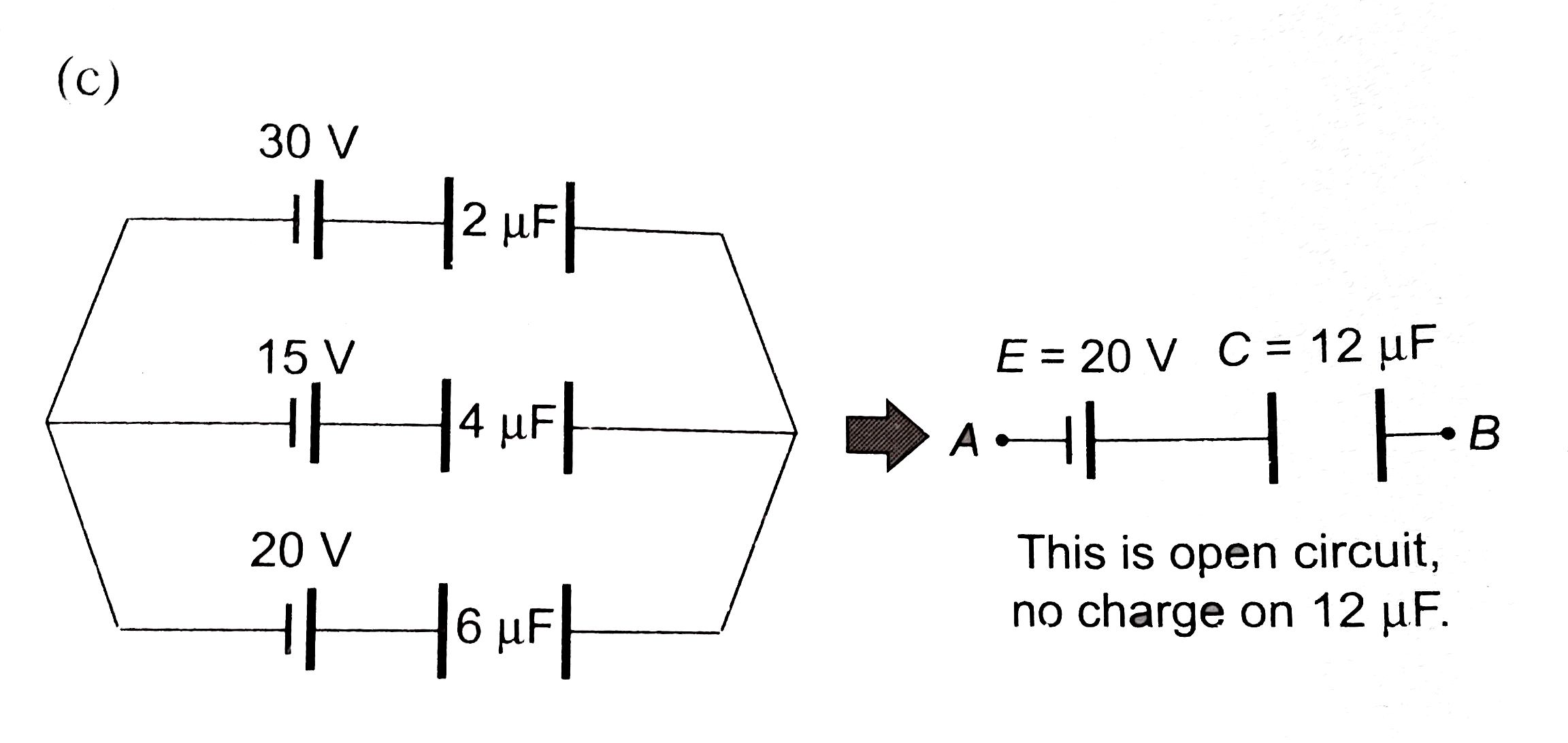
E=30×2+15×4+20×62+4+6=20V
C=2+4+6=12μF
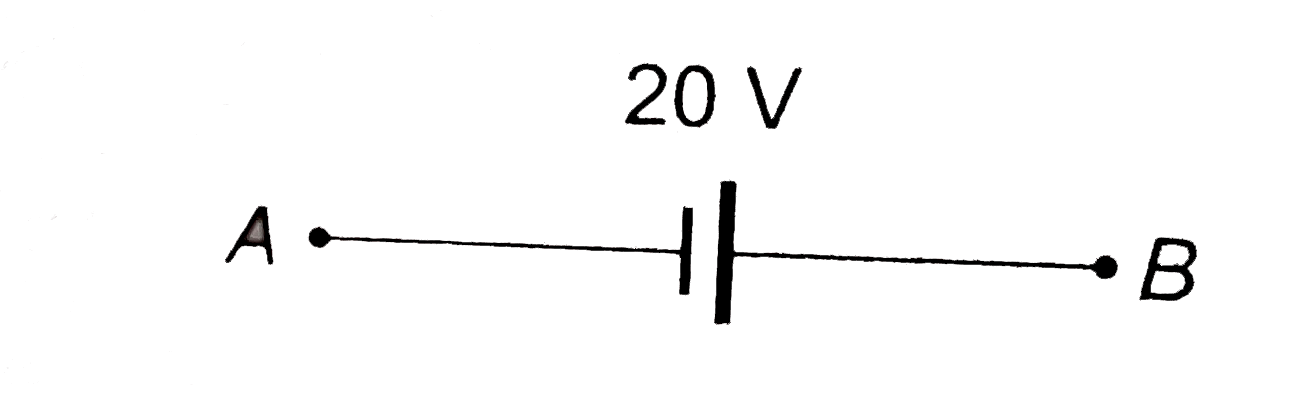
VB−VA=20V
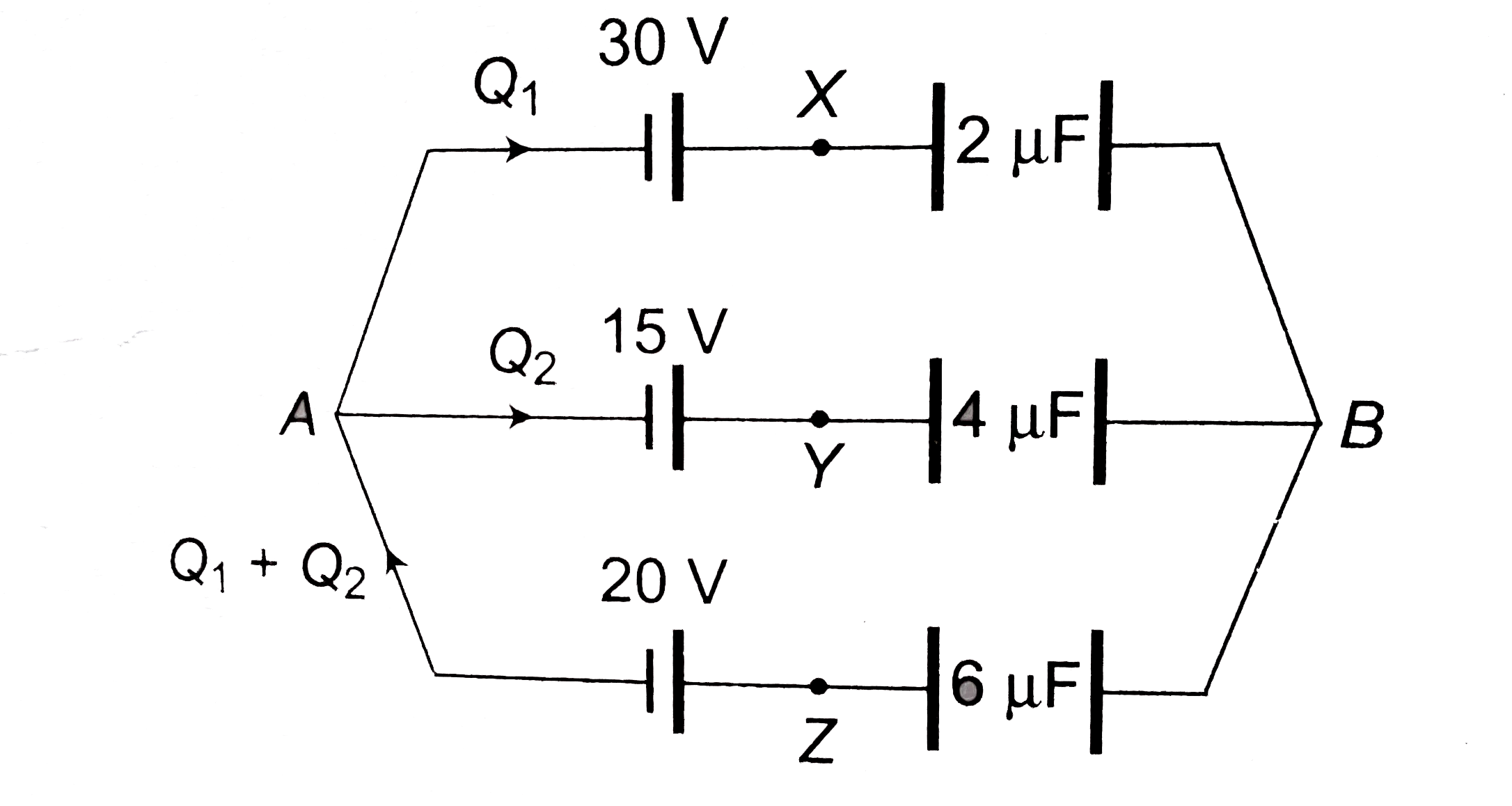
AXB :
VA+30−Q12=VB⇒VA−VB+30=Q12
−20+30=Q12⇒Q1=20μC
AYB :
VA+15−Q24=VB⇒VA−VB+15=Q24
−20+15=Q24⇒Q2=−20μC
Check AZB :
VA+20−Q1+Q26=VB
VA−VB+20=Q1+Q26
−20+20=Q1+Q26
Q1+Q2=0.
|
Topper's Solved these Questions
Similar Questions
Find the charges on the three capacitors shown in figure

View SolutionFind the charges on the three capacitors shown in figure

View SolutionFind the charges on the three capacitors shown in figure
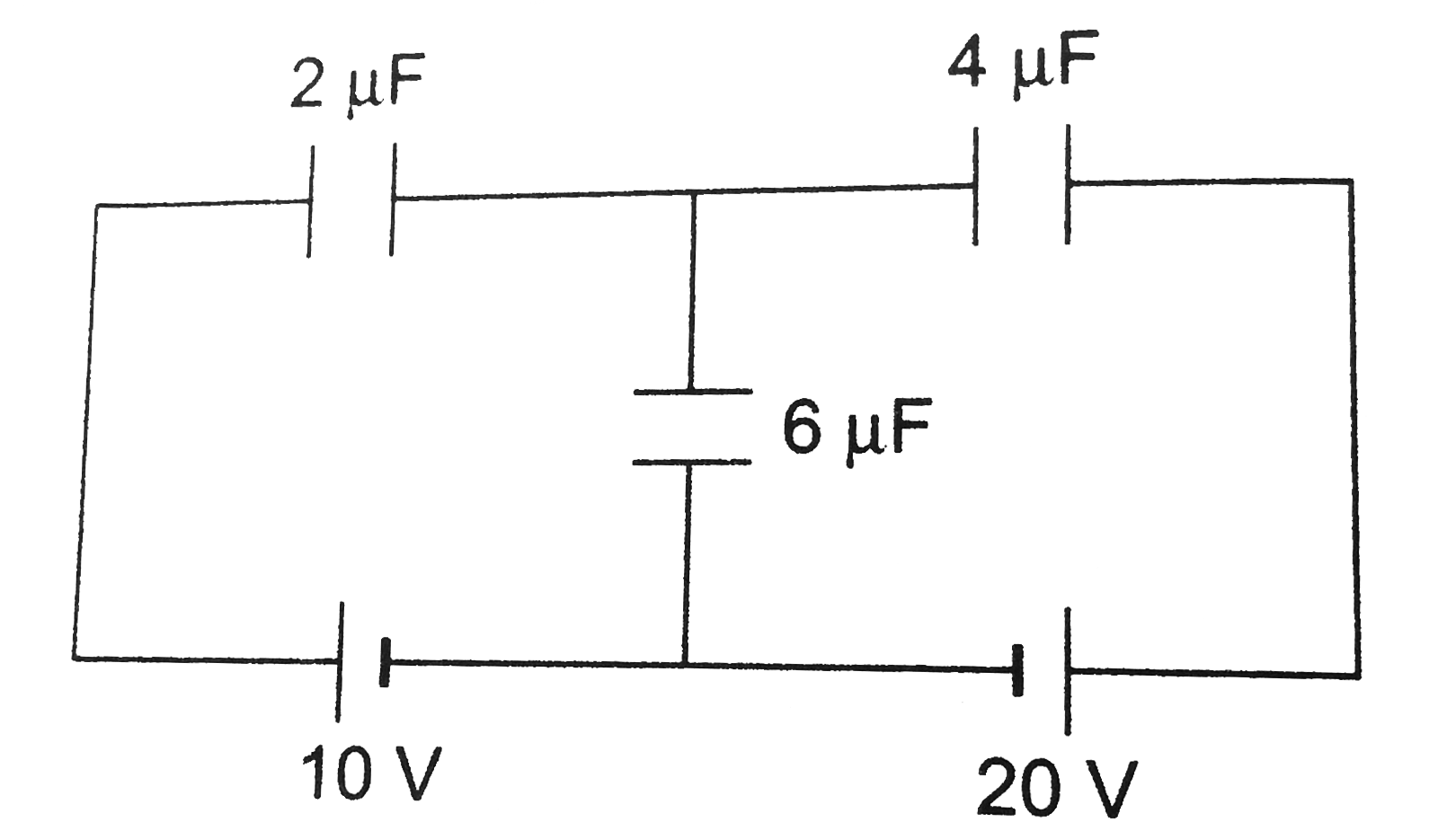
View SolutionFind the charges on the three capacitors shown in figure

View SolutionFind the charges on the three capacitors shown in figure

View SolutionFind the charges on the three capacitors shown in figure

View SolutionFind the charge on the capacitor shown in figure
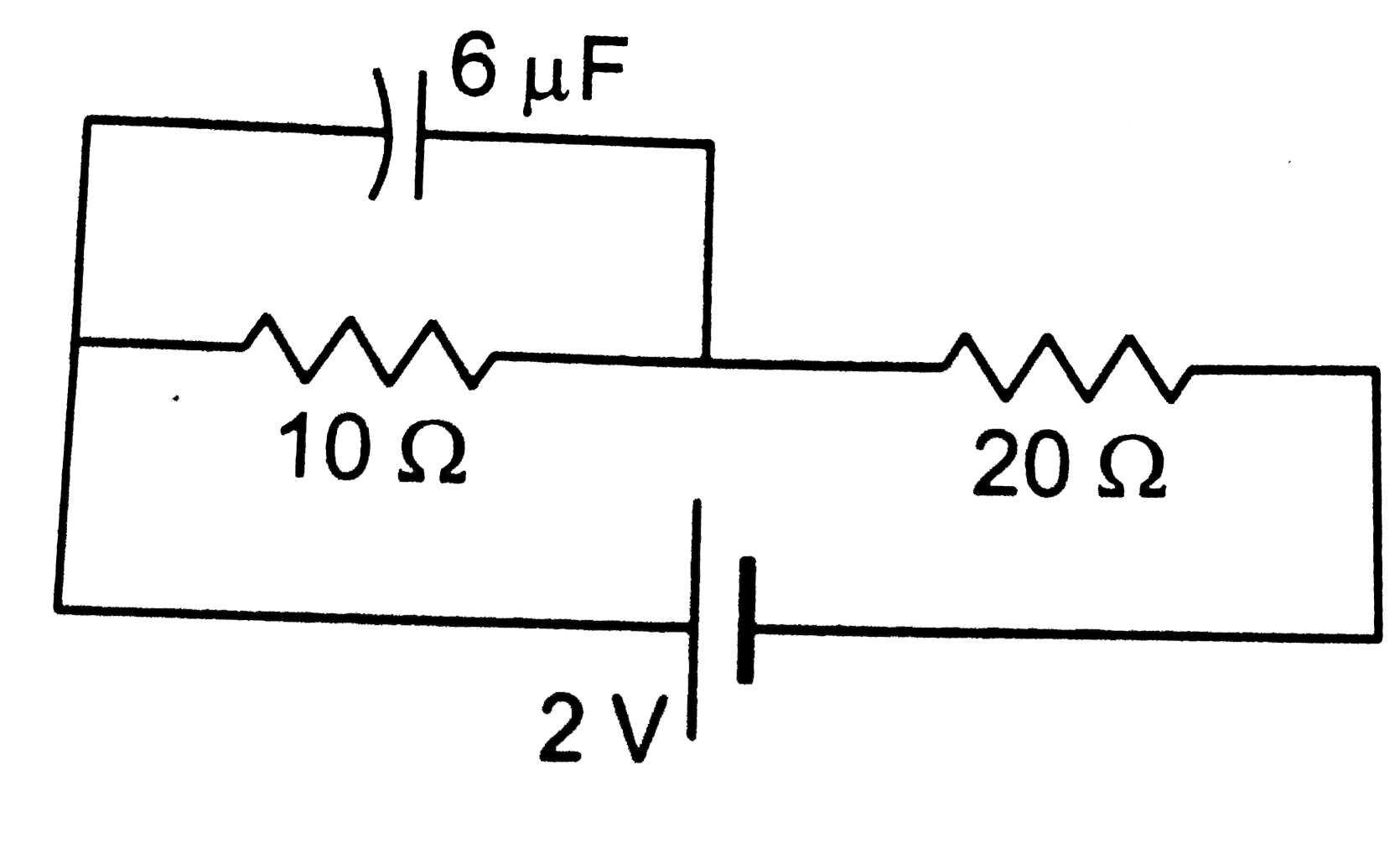
View SolutionFind the charge on the capacitor shown in figure

View SolutionCalcuate the charge on each capacitor shown in figure
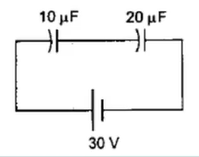
View SolutionThe charge on 3μF capacitor shown in the figure is
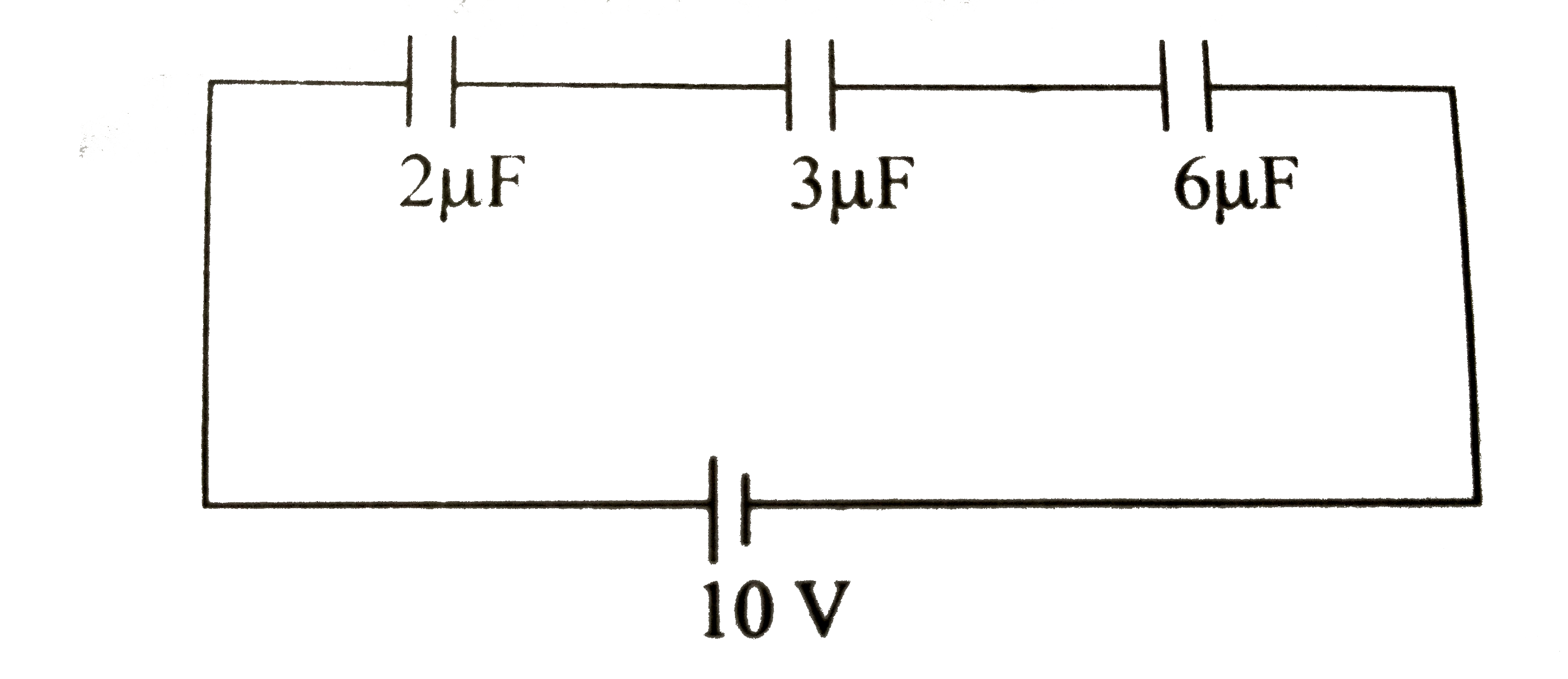
View Solution
