A material of resistivity ρ is formed in the shape of a truncated cone of altitude h as shown in the figure. The top end has radius a while bottom b. Assuming a uniform current density through any circular cross-section of the cone, the resistance between two ends is :
 .
.
ρhab
ρhπab
ρaπhb
ρbπah
The correct Answer is:B
For frustum of cone, A=√A1A2=√πa2.πb2=πab
R=ρhA=ρhπab.
Topper's Solved these Questions
Similar Questions
A conductor having resistivity ρ is bent in the shape of a half cylinder as shown in the figure. The inner and outer radii of the cylinder are aandb respectively and the height of the cylinder is h. A potential difference is applied across the two rectangular faces of the conductor. Calculate the resistance offered by the conductor.
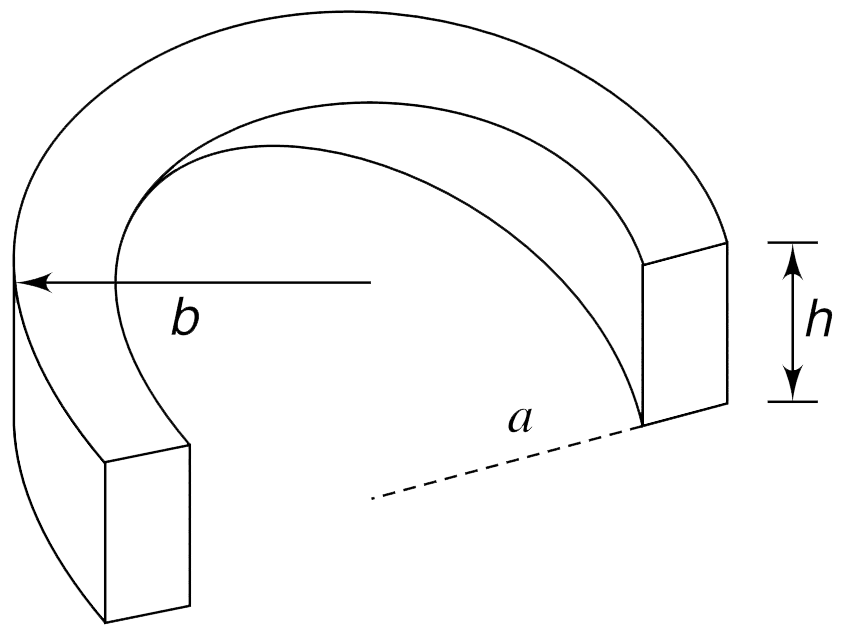 View Solution
View SolutionTwo long straight cylindrical conductors with resistivities ρ1andρ2 repectively are joined together as shown in figure . The radius of each of the conductor is a . If a uniform total current I flows through the conductors , the magnitude of the total free charge at the interface of the two conductor is
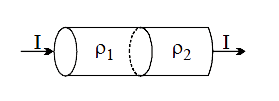 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.
 A2πB1πCπDπ2
A2πB1πCπDπ2 - Question 2 - Select One
A glass capillary tube is of the shape of a truncated cone with an apex angle α so that its two ends have cross sections of different radii. When dipped in water vertically, water rises in it to a high h, where the radius of its cross section is b. If the surface tension of water is S, its density if ρ, and its contact angle with glass is θ, the value of h will be (g is the acceleration due to gravity)
 A(a) 2Sbρgcos(θ−α)B(b) 2Sbρgcos(θ+α)C(c) 2Sbρgcos(θ−α/2)D(d) 2Sbρgcos(θ+a/2)
A(a) 2Sbρgcos(θ−α)B(b) 2Sbρgcos(θ+α)C(c) 2Sbρgcos(θ−α/2)D(d) 2Sbρgcos(θ+a/2) - Question 3 - Select One
A conductor of resistivity ρ and resistance R, as shown in the figure, is connected across a battery of emf V. Its radius varies from a at left end to b at right end. The electric field at a point P at distance x from left end of it is
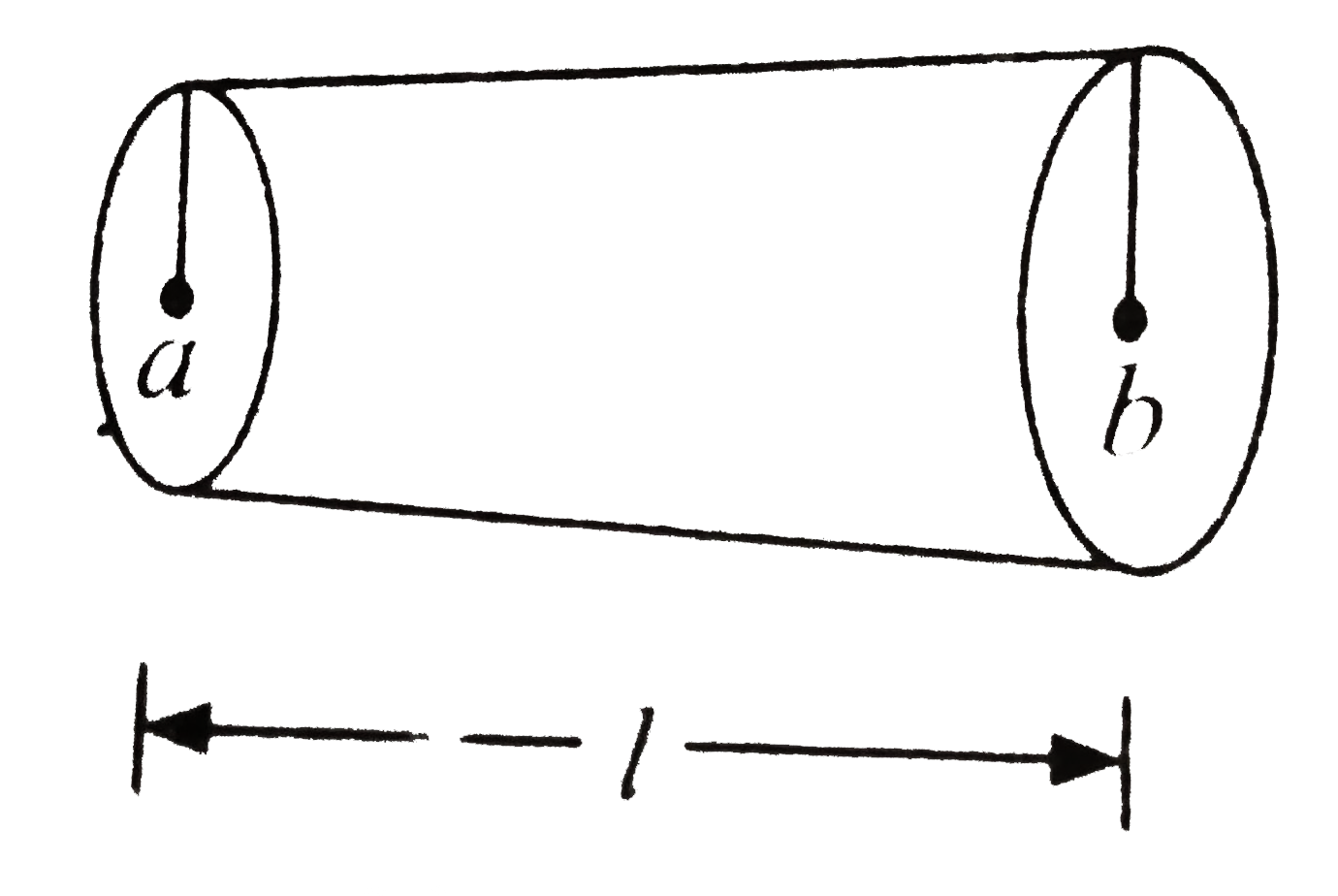 AVI2ρπR[Ia+(b−a)x]2B2VI2ρπR[Ia+(b+a)x]2CVI2ρ2πR(Ia+(b−a)x)2Dnone of these
AVI2ρπR[Ia+(b−a)x]2B2VI2ρπR[Ia+(b+a)x]2CVI2ρ2πR(Ia+(b−a)x)2Dnone of these
A resistance is in the shape of a turnacated right circuit cone The radit are a and b (b>a) the special resistance of the material is p and the alitude is h If laper is small then find the resistance between the plate faces of the resistor
View SolutionA conducting wire of length 'I', area of cross-section A and electric resistivity ρ is connected between the terminals of a battery. A potential difference V is developed between its ends, causing an electric current.
If the length of the wire of the same material is doubled and the area of cross-section is halved, the resultant current would be:View SolutionA conducting plate of thickness t is in the shape of an arc. Its inner and outer rim form a 30∘ arc of radius r and 2r respectively at point O (see figure). Electric current flows through the strip along circular arcs as indicated in the diagram. find resistance of the plate if its material has conductivity σ.
 View Solution
View Solution(a) What are the readings of the ammeters A1 and A2 shown in the figure.neglect the resistance of the meters.
(b) Calculate the current through the circuit and the potential difference across the diode shown in the figure. The drift current fo the diode is 20μA.
(c ) Each of the resistances shown in the figure has a value of 20Ω. find the equivalent resistance between A and B. Does it depend on whether the point A or B is at higher potential?
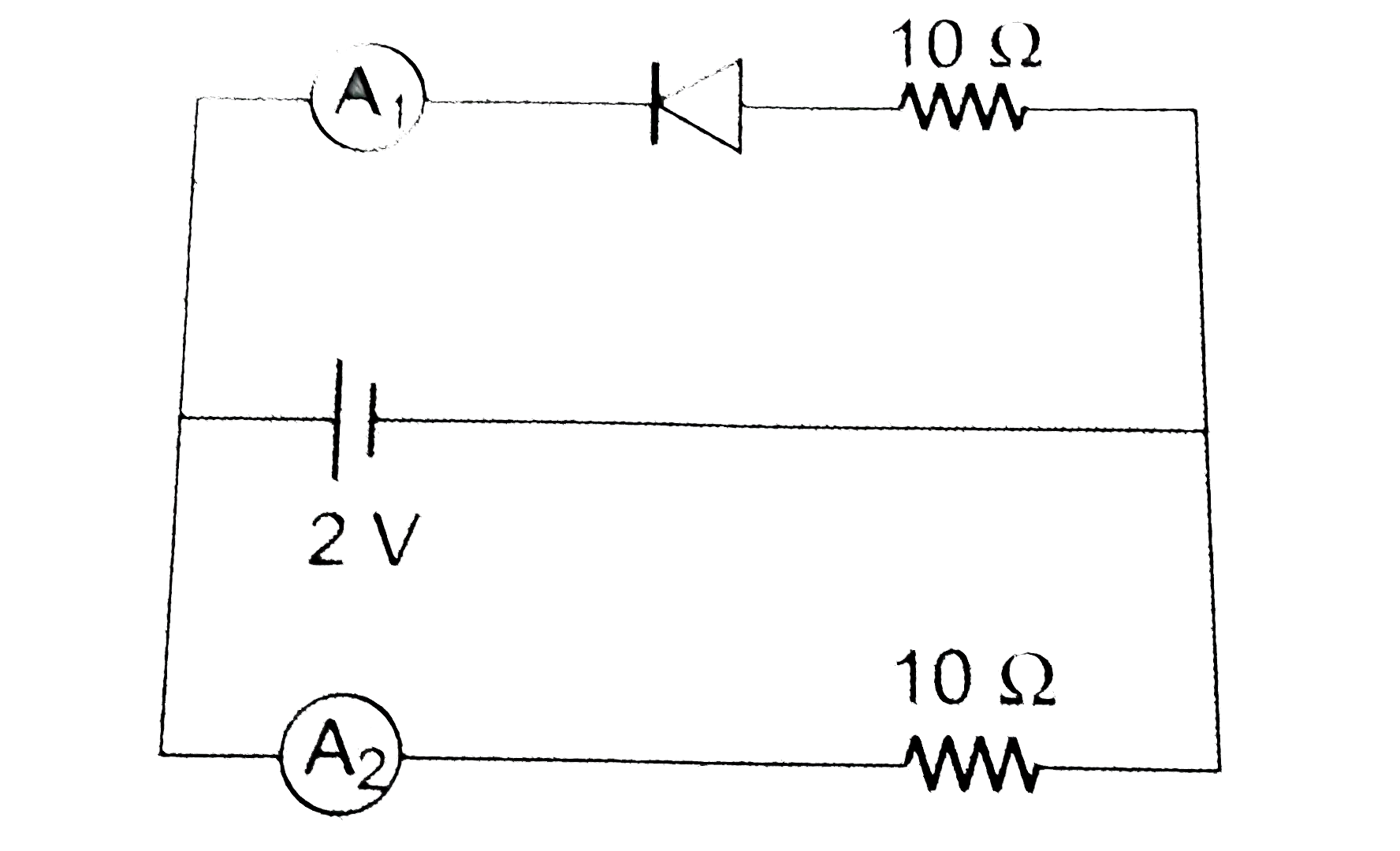
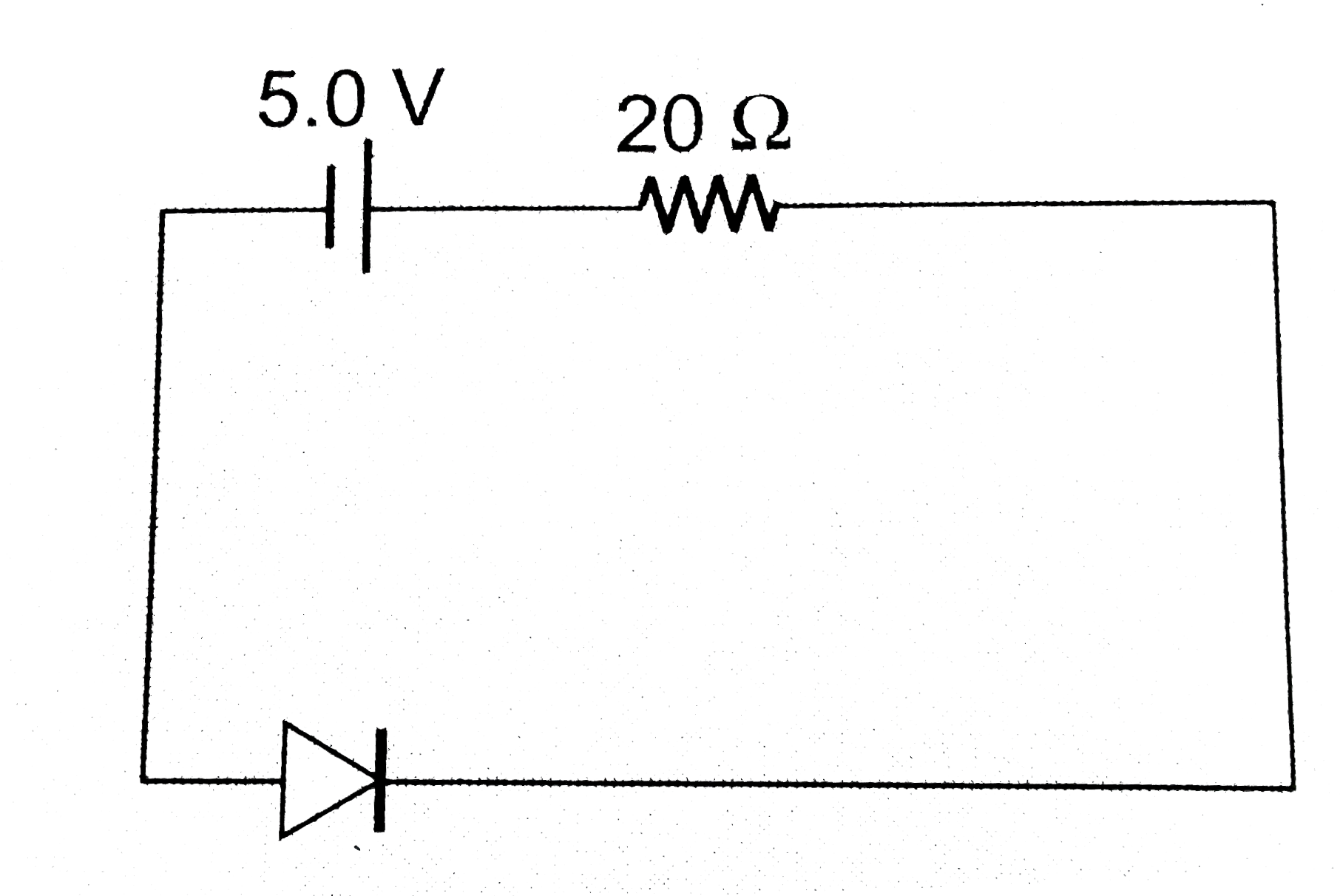
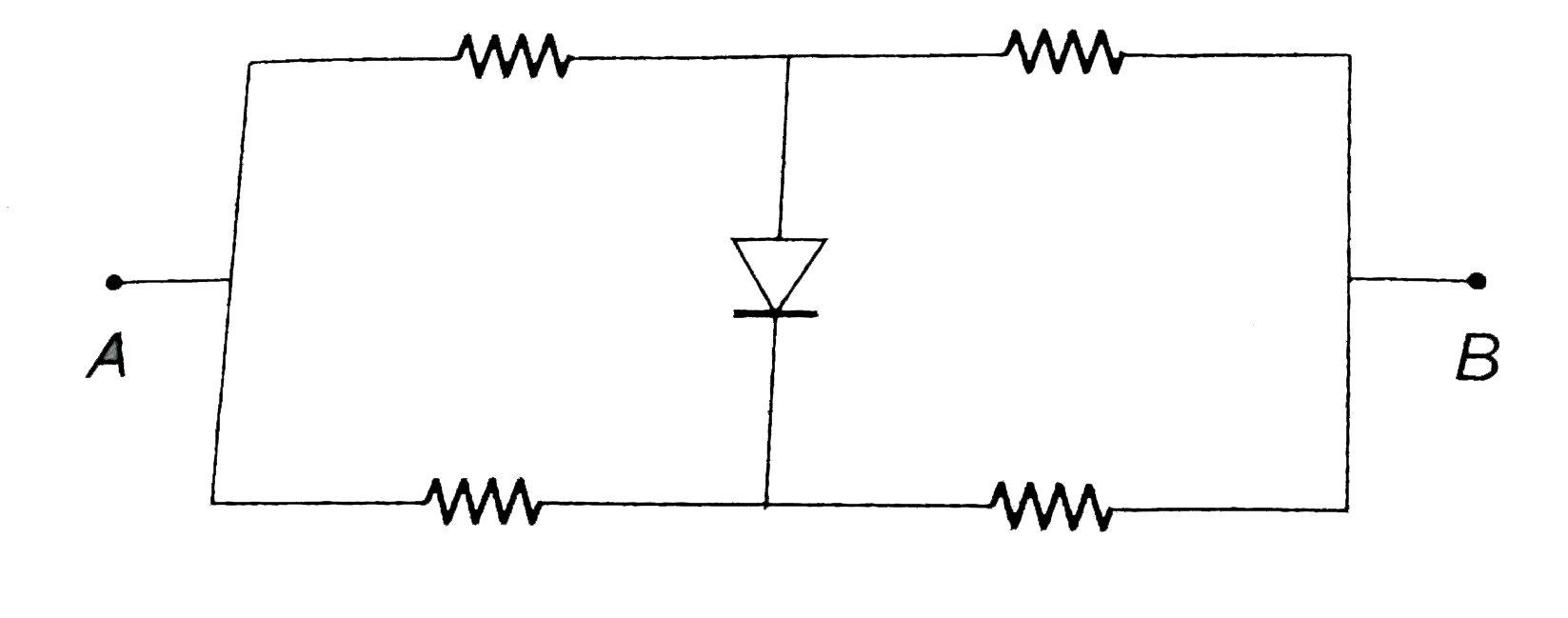 View Solution
View SolutionTwo conducting wires A and B are made of same material. If the length of B is twice that of A and the radius of circular cross-section of A is twice that of B, then resistances RA and RB are in the ratio
View Solution

