Find the electric potential energy of a unifomly charged then spherical shell.
To find the electric potential energy of a uniformly charged thin spherical shell, we can follow these steps:
Step 1: Define the parameters
Let the radius of the spherical shell be R and the total charge on the shell be Q0.
Step 2: Determine the electric potential at the surface of the shell
The electric potential V at the surface of a uniformly charged spherical shell is given by the formula:
V=Q04πϵ0R
where ϵ0 is the permittivity of free space.
Step 3: Calculate the self-energy of the shell
The self-energy Us of the charged shell can be calculated by integrating the potential over the charge distribution. The self-energy is given by:
Us=∫Q00Vdq
Substituting the expression for V:
Us=∫Q00Q04πϵ0Rdq
Step 4: Perform the integration
Since V is constant with respect to q during the integration, we can take it out of the integral:
Us=Q04πϵ0R∫Q00dq
The integral ∫Q00dq evaluates to Q0:
Us=Q04πϵ0R⋅Q0=Q204πϵ0R
Final Result
Thus, the electric potential energy of a uniformly charged thin spherical shell is:
Us=Q204πϵ0R
---
Let the radius of the spherical shell be R and the total charge on the shell be Q0.
The electric potential V at the surface of a uniformly charged spherical shell is given by the formula:
V=Q04πϵ0R
where ϵ0 is the permittivity of free space.
The self-energy Us of the charged shell can be calculated by integrating the potential over the charge distribution. The self-energy is given by:
Us=∫Q00Vdq
Substituting the expression for V:
Us=∫Q00Q04πϵ0Rdq
Since V is constant with respect to q during the integration, we can take it out of the integral:
Us=Q04πϵ0R∫Q00dq
The integral ∫Q00dq evaluates to Q0:
Us=Q04πϵ0R⋅Q0=Q204πϵ0R
Thus, the electric potential energy of a uniformly charged thin spherical shell is:
Us=Q204πϵ0R
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise
155 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
Find the electric potential energy of a uniformly charged sphere.
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionFind the electric potential energy of the system of charges
View SolutionA point charge +Q is placed at the centre of an isolated conducting shell of radius R. Find the electrostatic potential energy stored outside the spherical shell if the shell also contains charge +Q distributed uniformly over it.
View SolutionFind out energy stored in the electric field of uniformly charged thin spherical shell of total charge Q and radius R.
View SolutionState Gauss's theorem in electrostatics. Apply this theorem to derive an expression for electric field intensity at a point outside a uniformly charged thin spherical shell.
View SolutionSketch the electric field lines for a unifomly charged hollow cylinder shown in Fig.
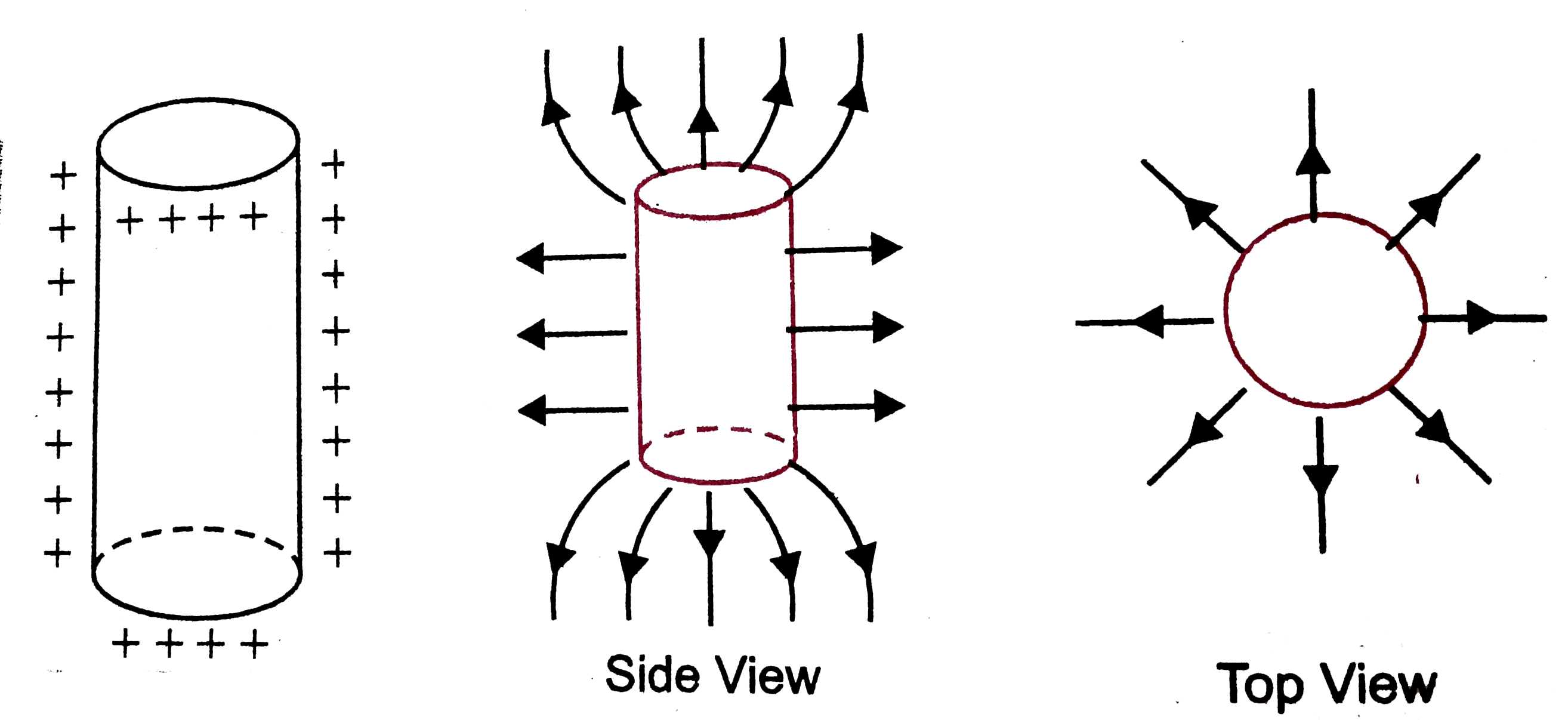
View SolutionSketch the electric field lines for a unifomly charged hollow cylinder shown in Fig.

View SolutionThe point charge is placed outside a spherical shell as shown i the figure. Find the electric potential (in kilo volt) on the surface of shell (Take: q=1μc and R=50cm)

View SolutionAssertion : Spherical shell a in the shown figure has a charge −q and shell B has charge +q. When these two are connected by a thin conducting wire, then whole of the electrostatic potential energy stored between the shell is lost.
Reason : Whole of the inner charge will transfer to outer shell B.
View Solution

