Assertion : Spherical shell a in the shown figure has a charge −q and shell B has charge +q. When these two are connected by a thin conducting wire, then whole of the electrostatic potential energy stored between the shell is lost.
Reason : Whole of the inner charge will transfer to outer shell B.
If both Assertion and Reason are true and Reason is the correct explanation of Assertion.
If both Assertion and Reason are true but Reason is not correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:A
To solve the question, we need to analyze the assertion and reason provided regarding the electrostatic potential energy between two charged spherical shells when they are connected by a conducting wire.
1. Understanding the Charges on the Spherical Shells:
- Shell A has a charge of −q.
- Shell B has a charge of +q.
2. Connecting the Shells:
- When the two shells are connected by a thin conducting wire, charge can flow between them until they reach the same potential.
3. Electrostatic Potential Energy:
- The electrostatic potential energy U between two point charges (or spherical shells) can be expressed as:
U=14πϵ0q1q2R
- Here, q1=−q and q2=+q, and R is the distance between the centers of the two shells.
4. Calculating Initial Potential Energy:
- Substituting the values into the formula:
U=14πϵ0(−q)(+q)R=−q24πϵ0R
- The negative sign indicates that the energy is attractive.
5. Charge Neutralization:
- When the shells are connected, the negative charge from shell A will neutralize the positive charge on shell B.
- The total charge after connection will be:
−q+q=0
6. Final Potential Energy:
- With a total charge of 0, the potential energy U between the shells becomes:
U=0
- Therefore, all the initial electrostatic potential energy is lost.
7. Conclusion:
- The assertion states that the whole of the electrostatic potential energy stored between the shells is lost, which is correct.
- The reason states that the whole of the inner charge will transfer to the outer shell B, which is also correct as the charges neutralize each other.
Final Answer:
Both the assertion and reason are correct, and the reason correctly explains the assertion.
- Shell A has a charge of −q.
- Shell B has a charge of +q.
- When the two shells are connected by a thin conducting wire, charge can flow between them until they reach the same potential.
- The electrostatic potential energy U between two point charges (or spherical shells) can be expressed as:
U=14πϵ0q1q2R
- Here, q1=−q and q2=+q, and R is the distance between the centers of the two shells.
- Substituting the values into the formula:
U=14πϵ0(−q)(+q)R=−q24πϵ0R
- The negative sign indicates that the energy is attractive.
- When the shells are connected, the negative charge from shell A will neutralize the positive charge on shell B.
- The total charge after connection will be:
−q+q=0
- With a total charge of 0, the potential energy U between the shells becomes:
U=0
- Therefore, all the initial electrostatic potential energy is lost.
- The assertion states that the whole of the electrostatic potential energy stored between the shells is lost, which is correct.
- The reason states that the whole of the inner charge will transfer to the outer shell B, which is also correct as the charges neutralize each other.
Both the assertion and reason are correct, and the reason correctly explains the assertion.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (A) Chapter exercises
227 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
A point charge +Q is placed at the centre of an isolated conducting shell of radius R. Find the electrostatic potential energy stored outside the spherical shell if the shell also contains charge +Q distributed uniformly over it.
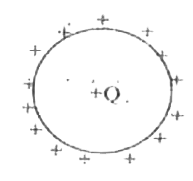
View SolutionTwo concentric spherical conducting shells of radii R and 2R are carrying charges q and 2q, respectively. Both are now connected by a conducting wire. Find the change in electric potential (inV) on the outer shell.
View SolutionConsider two concentric metalic shell's of radii R and 2R. The inner shell is having charge Q and outer shell is uncharged. If they are connected with a conducting wire. Then,
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R/2 from the centre of the shell is
View SolutionTwo concentric spherical conducting shells of radii r and R (r<R) carry charges q and Q respectively . The two shells are now connected by a conducting wire. The final charge on the inner shell is
View SolutionA solid metallic sphere of radius a is surrounded by a conducting spherical shell of radius b(b>a). The solid sphere is given a charge Q. A student measures the potential at the surface of the solid sphere as V and the potential at the surface of spherical shell as Vb. After taking these readings, he decides . to put charge of −4Q on the shell. He then noted the readings of the potential of solid sphere and the shell and found that the potential difference is △V .
He then connected the outer spherical shell to the earth by a conducting wire and found that the charge on the outer surface of the shell as He then decides to remove the earthing connection from the shell and earthed the inner solid sphere. Connecting the inner sphere with the earth he observes the charge on the solid sphere as q2. He then wanted to check what happens if the two are connected by the conducting wire. So he removed the earthing connection and connected a conducting wire between the solid sphere and the spherical shelll. After the connections were made he found the charge on the outer shell as q3.
Potential difference (△CV) measured by the student between the inner solid shere and outer shell after putting a charge −4Q is
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionIn the figure shown the elctric potential energy of the system is : (q is at the centre of the conducting neutral spherical shell of inner radius a and outer radius b)

View SolutionA solid metallic sphere of radius a is surrounded by a conducting spherical shell of radius b(b>a). The solid sphere is given a charge Q. A student measures the potential at the surface of the solid sphere as V and the potential at the surface of spherical shell as Vb. After taking these readings, he decides . to put charge of −4Q on the shell. He then noted the readings of the potential of solid sphere and the shell and found that the potential difference is △V .
He then connected the outer spherical shell to the earth by a conducting wire and found that the charge on the outer surface of the shell as He then decides to remove the earthing connection from the shell and earthed the inner solid sphere. Connecting the inner sphere with the earth he observes the charge on the solid sphere as q2. He then wanted to check what happens if the two are connected by the conducting wire. So he removed the earthing connection and connected a conducting wire between the solid sphere and the spherical shelll. After the connections were made he found the charge on the outer shell as q3.
q2 is
View Solution
