Find the equivalent cappacitance between $A$ and $B$ .
(a) Three conducting concentic shells of radii $r, 2 r$ and
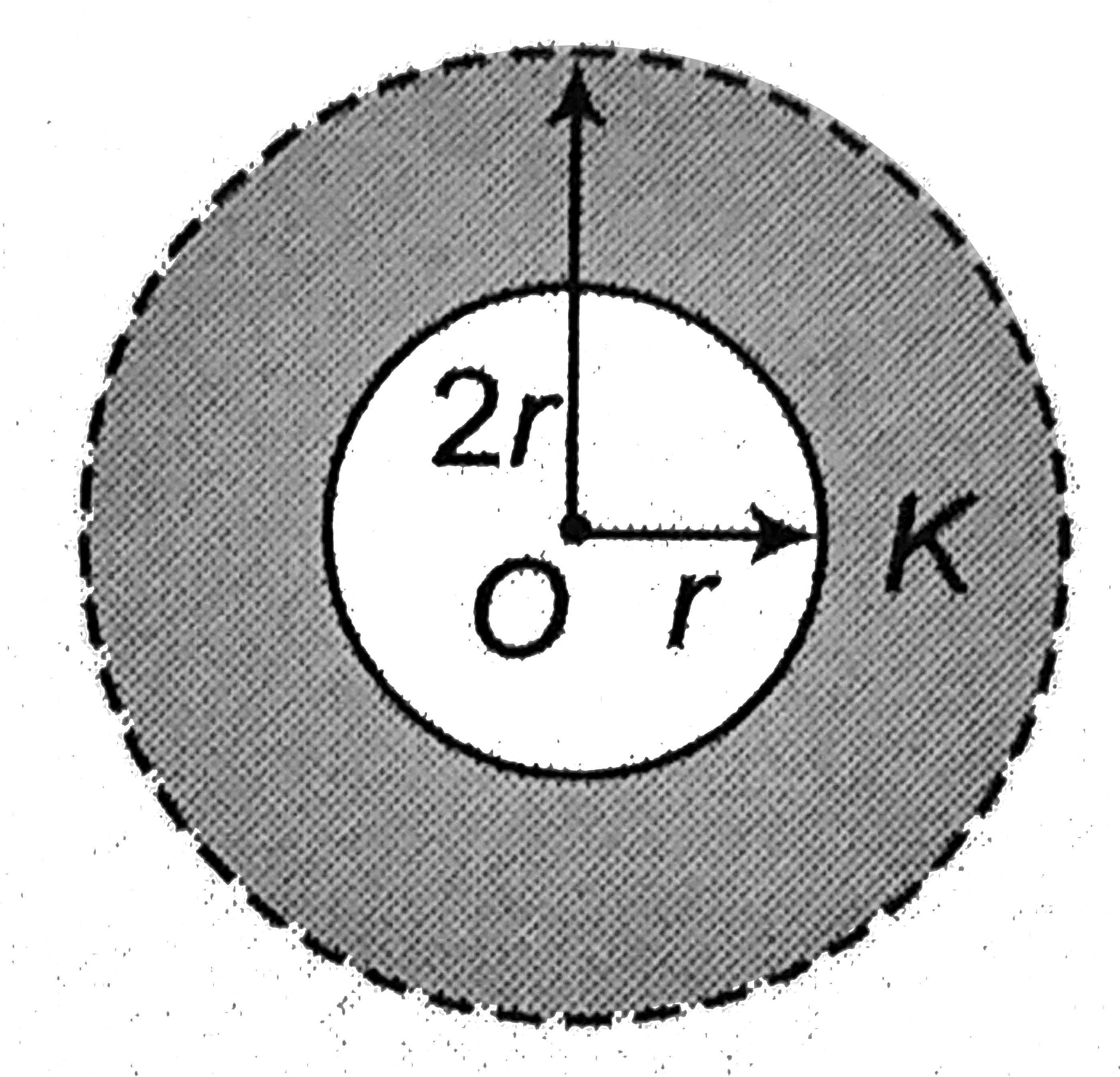
(b) An isoltated ball-shaped conductor of radius $r$ surrounded by an adjuacent layer of dielectric $(K)$ and outer radius $2 r$ .
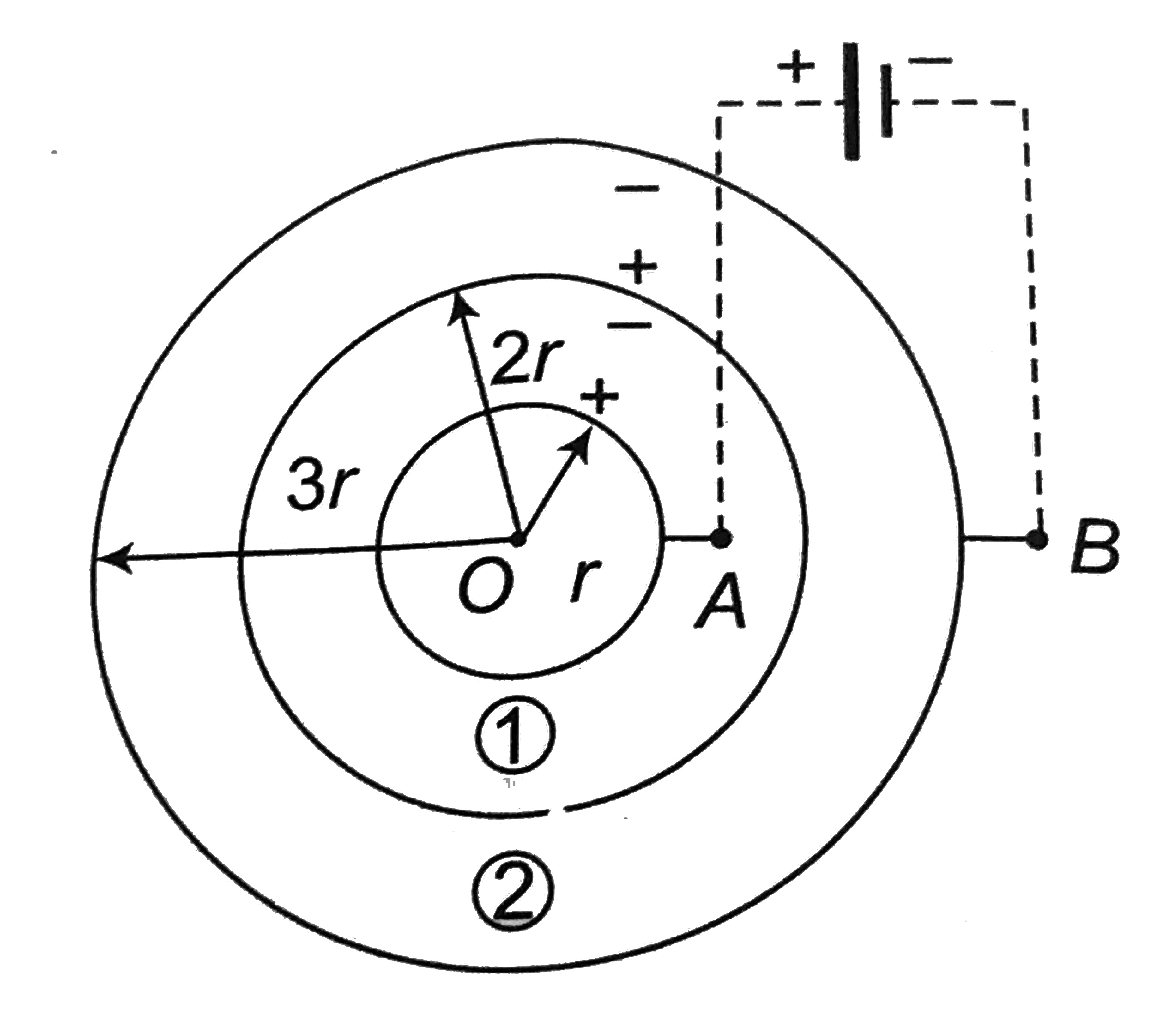
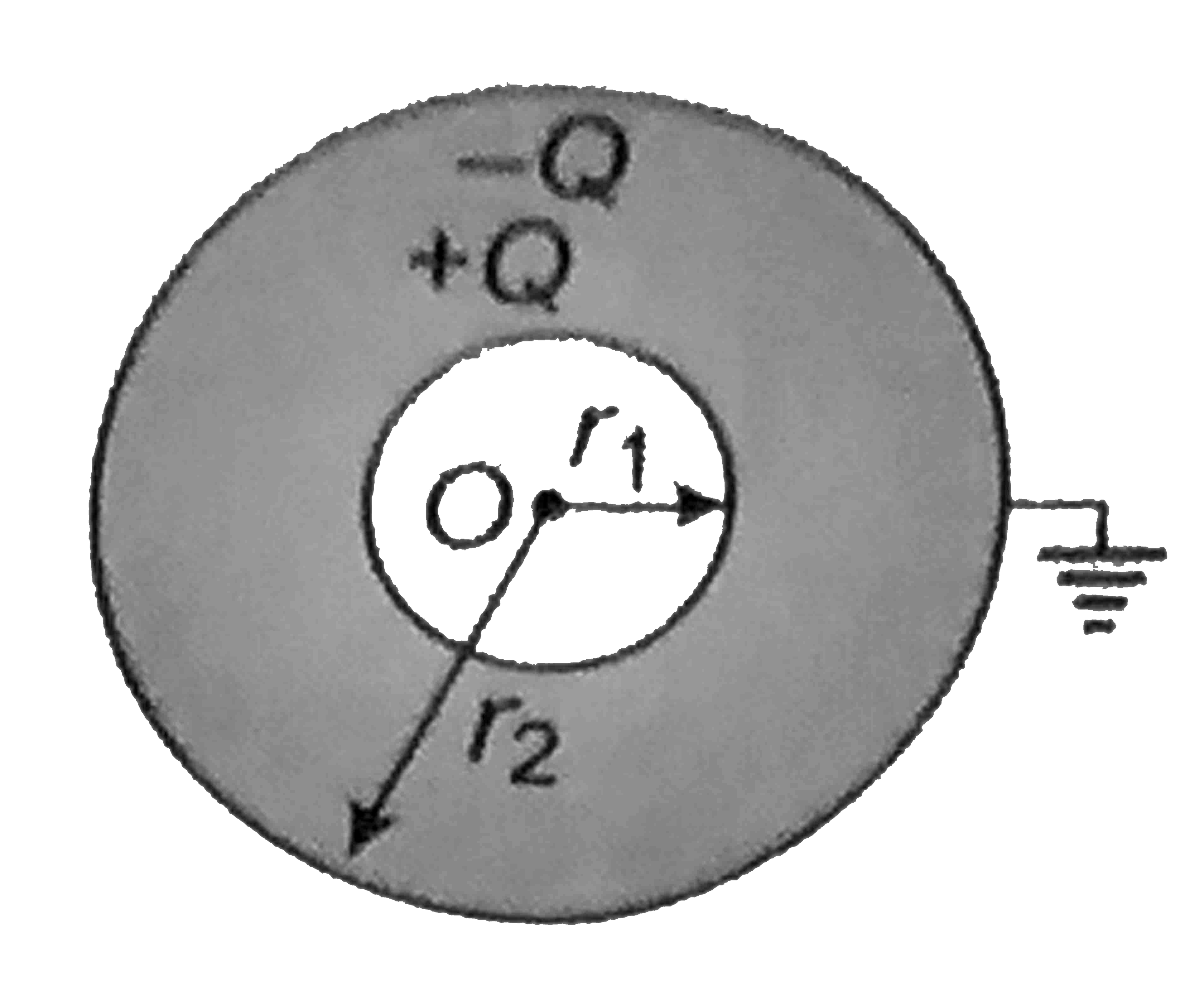
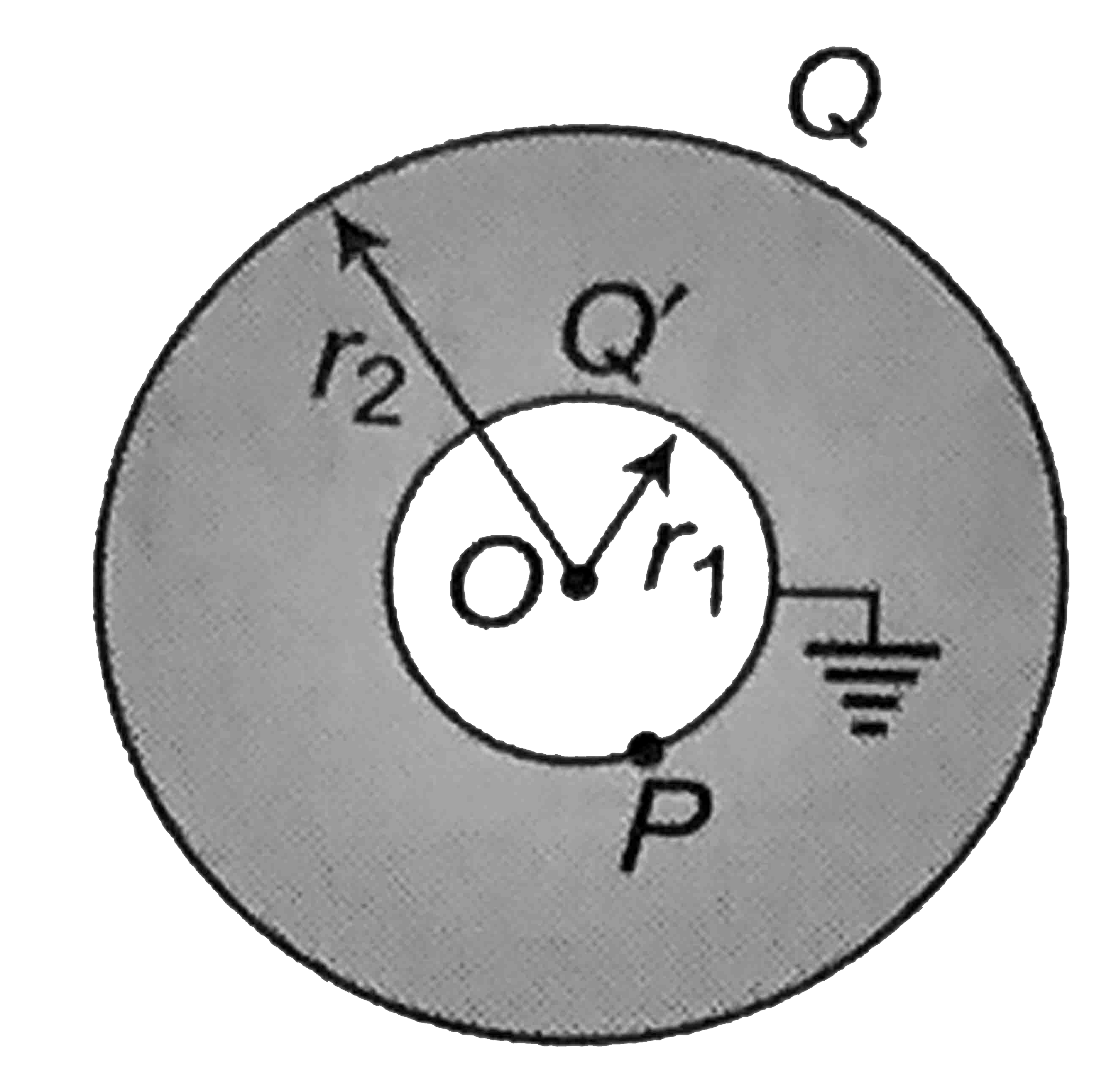
Two conducting concentic spherical shells having radii $r_{1}$ and $r_{2} (r_{2} > r_{1})$ , calculate capacity of the system if
(i) The inner shell is given a charge and outer is connected to the earth.
(ii) The outer shell is given a charge and inner is connected to the earth.
(d) Find capacitance of the system
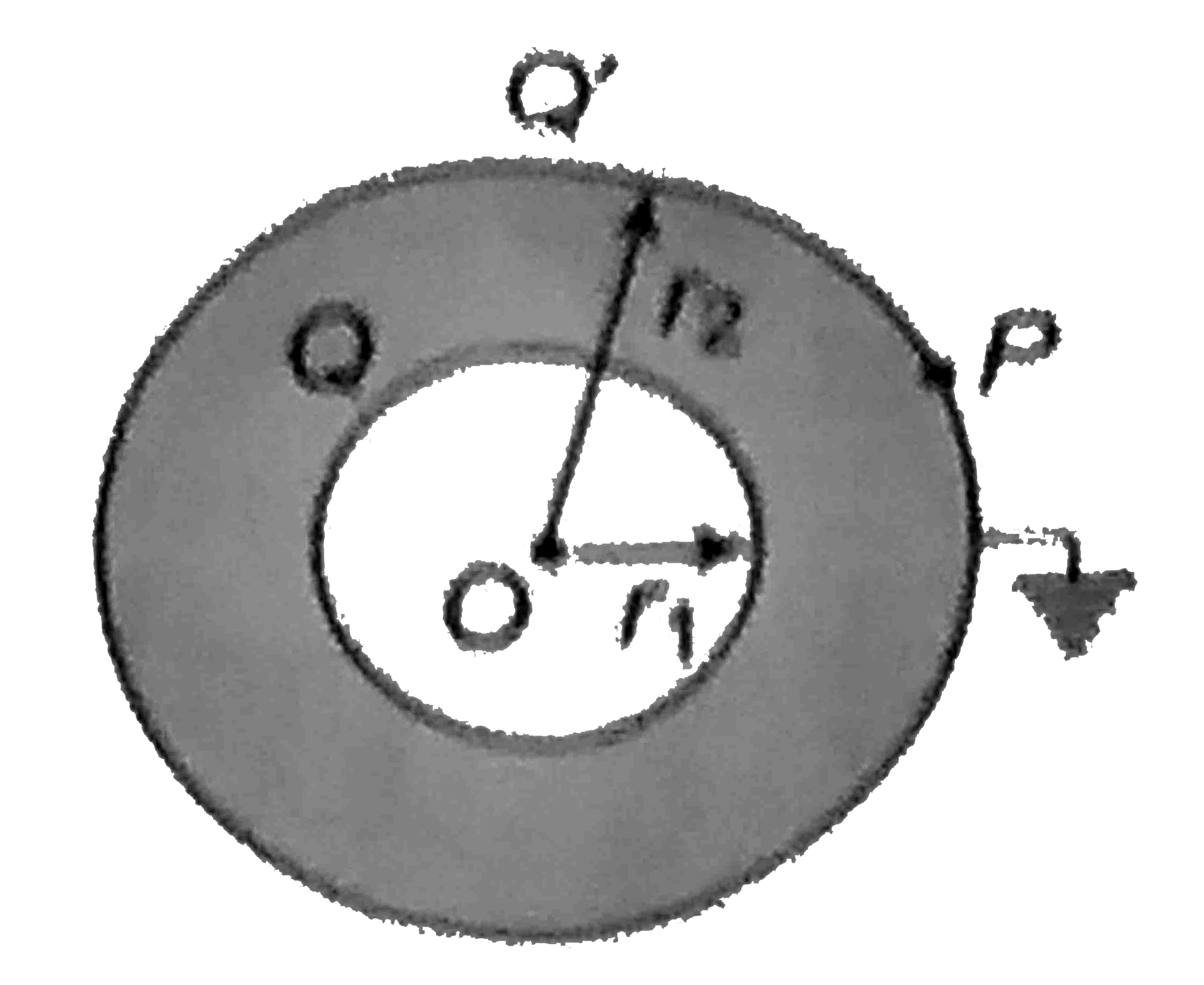
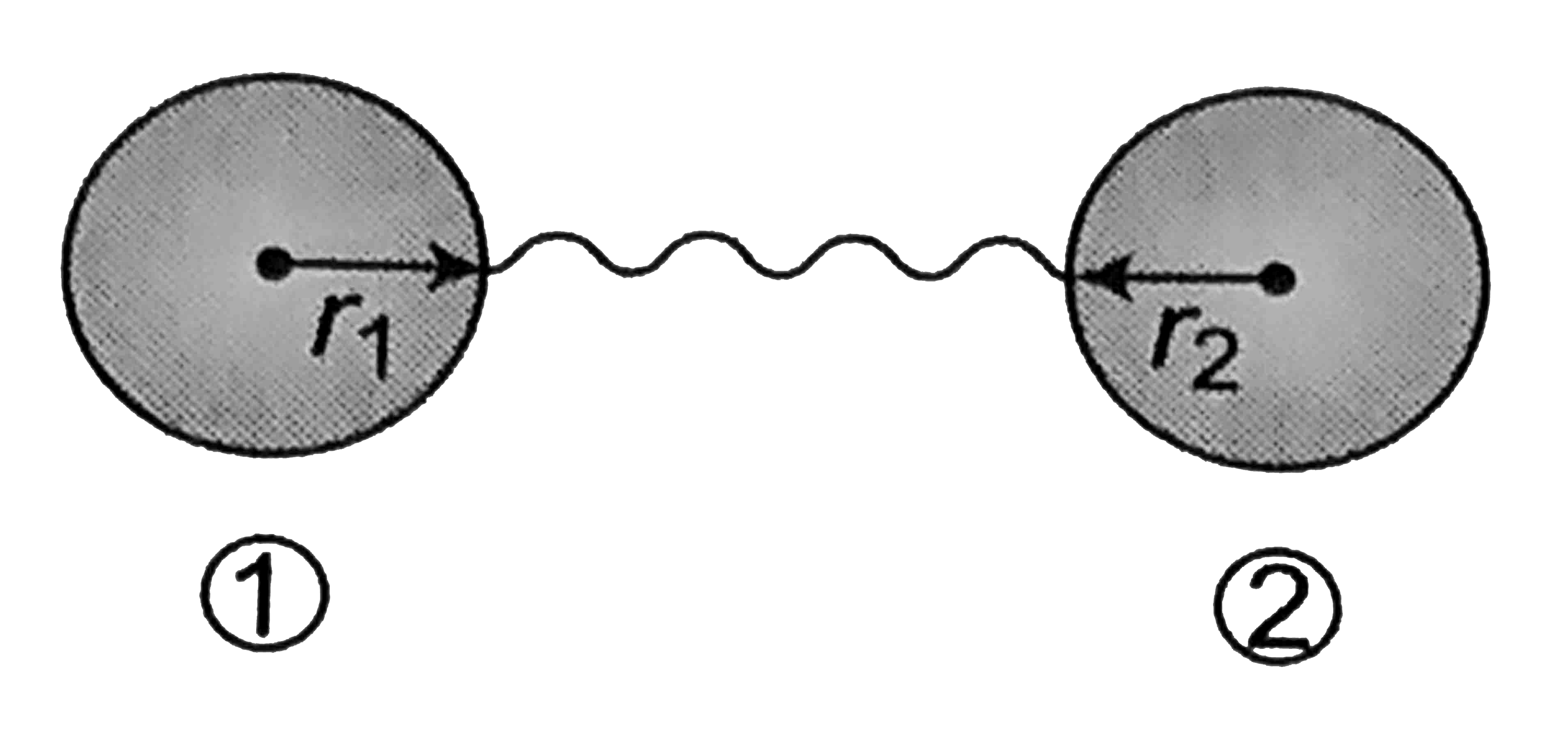
(i) Two shells of radii $r_{1}$ and $r_{2}$ having charges are connected by a metallic wire, the separation between shells is large.
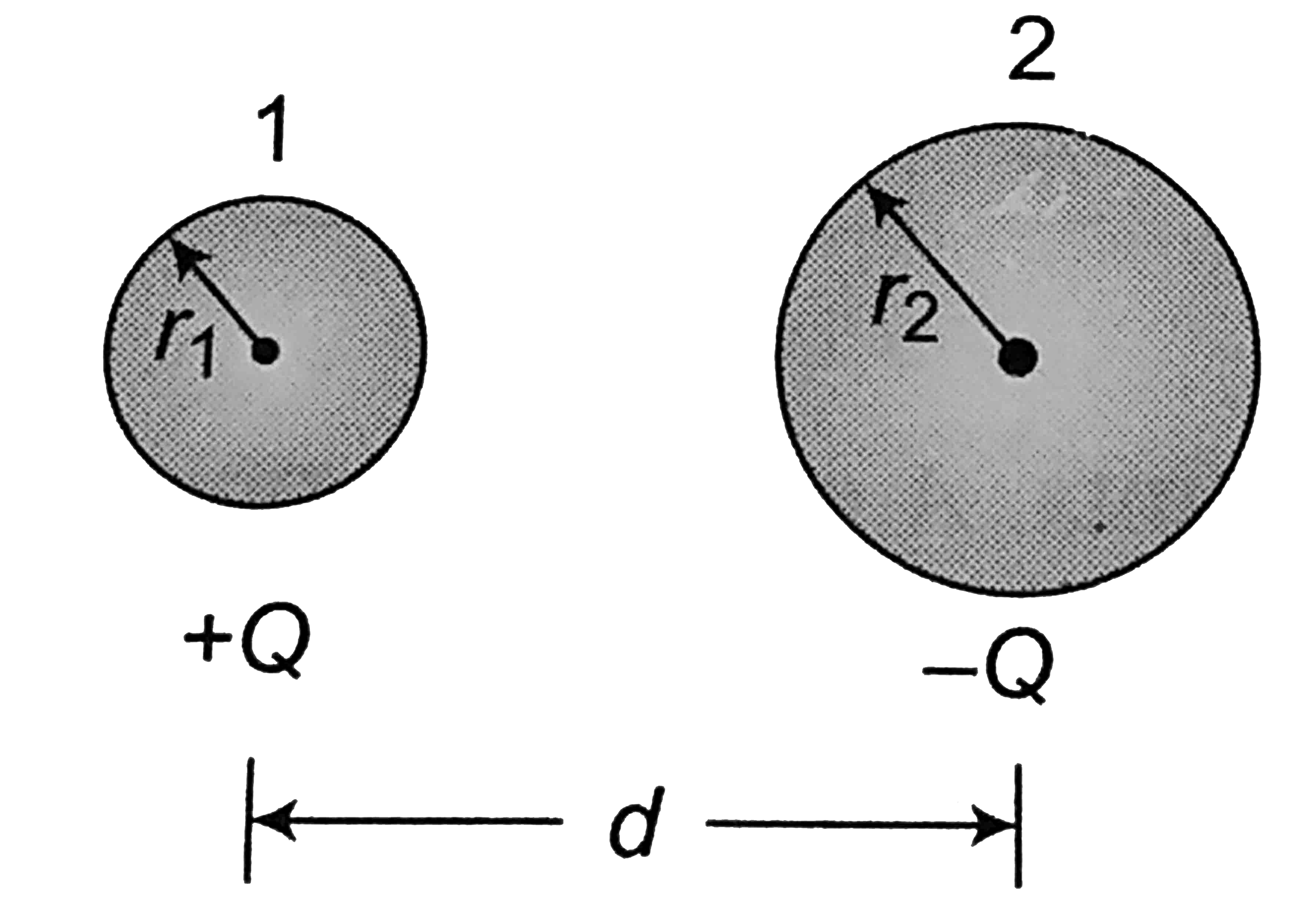
(ii) Two shells of radii $r_{1}$ and $r_{2}$ carry equal and opposite charges and are separated by a distance $d$ .

Text Solution

Verified by Experts

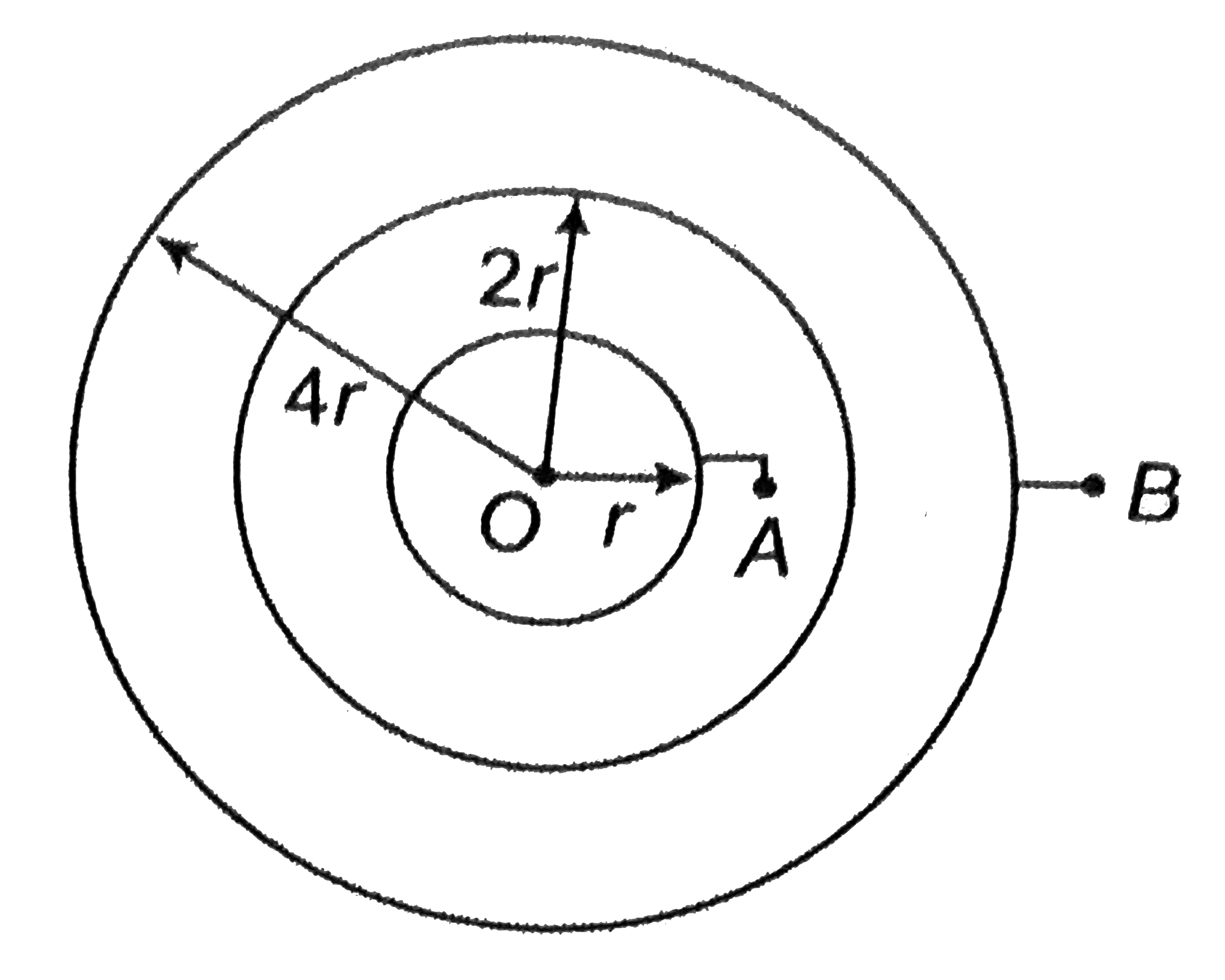
(a) Two capacitors,
Capacitor $1, C_{1} = \frac{4 π \in_{0} r .2 r}{(2 r - r)} = 8 π \in_{0} r$
Capacitor $2, C_{2} = \frac{4 π \in_{0} 2 r .3 r}{(3 r - 2 r)} = 24 π \in_{0} r$
connected a battery between $A$ and $B$ , and check polarity, $+, -, +, -,$ .
$C = \frac{C_{1} C_{2}}{C_{1} + C_{2}} = + π \in_{0} r$
(b) capacitor $1$ :
$C_{1} = \frac{4 π \in_{0} K . r .2 r}{2 r - r} = 8 π \in_{0} K r$
Capacitor $2$ : Isolated sphere of radius $2 r$ and outer radius infinite.
$C_{2} = 4 π \in_{0} 2 r = 8 π \in_{0} r$
$C_{1}$ and $C_{2}$ in series, as shown in $(a)$
$C - (e q) = \frac{C_{1} C_{2}}{C_{1} + C_{2}} = \frac{8 π \in_{0} K r}{K + 1}$
(c) (i) Let total charge on outer shell is $Q$ '
$V_{p} = \frac{1}{4 π \in_{0}} (\frac{Q}{r_{2}} + \frac{Q'}{r_{2}}) = 0 \Rightarrow Q' = - Q$
$C = \frac{4 π \in_{0} r_{1} r_{2}}{r_{20 - r - (1)}}$
(ii) Let charge on inner shell be $Q'$ .
$V_{p} = \frac{1}{4 π \in_{0}} (\frac{Q'}{r_{1}} + \frac{Q}{r_{2}}) = 0$
$Q' = \frac{- Q r_{1}}{r_{2}}$
This capacitor is combination of two capacitors
(i) capacitor $1, C_{1} = \frac{4 π \in_{0} r_{1} r_{2}}{r_{2} - r_{1}}$
(ii) Capacitor $2$ , $C_{2} = 4 π \in_{0} r_{2}$ (isolated spherical capacitor)
These capacitor are in parallel. the positive plates of capacitors are at one place. the $- v e$ plate of capacitor $1$ is connected to ground i.e., its potential is zero. the $- v e$ plate of capacitor $2$ is at infine i.e., its potential is zero. hence, positive plates at one point and negative plates at another point and hence $C_{1}$ and $C_{2}$ are in parallel.
$C_{e q} = C_{1} + C_{2} = 4 π \in_{0} r_{2} (\frac{r_{1}}{r_{2} - r_{1}} + 1) = \frac{4 π \in_{0} r_{2}^{2}}{(r_{2} - r_{1})}$
(d) (i) $C_{1} = 4 π \in_{0} r_{1}$
$C_{2} = 4 π \in_{0} r_{2}$
$C_{1}$ and $C_{2}$ are in parallel. their positive plates are connected as shown and negative plates are at infine.
$C_{e q} = C_{1} + C_{2} = 4 π \in_{0} (r_{1} + r_{2})$
(ii) Here, we will find capacitance with the help of energy. energy stored in a conductor,
$U = \frac{Q^{2}}{2 C}$
Energy of two point charges sepearated by $r$ ,
$U' = \frac{1}{4 π \in_{0}} \frac{Q_{1} Q_{2}}{r}$ so potential energy of system
$U = U_{1} + U_{2} + U_{12}$
$= \frac{Q^{2}}{2 C_{1}} + \frac{Q^{2}}{2 C_{2}} + \frac{1}{4 π \in_{0}} \frac{(Q) (- Q)}{d}$
$= \frac{Q^{2}}{2 \times 4 π \in_{0} r_{1}} + \frac{Q^{2}}{2 \times 4 π \in_{0} r_{2}} - \frac{Q^{2}}{(4 π \in_{0} d)}$
$= \frac{Q^{2}}{8 π \in_{0}} (\frac{1}{r_{1}} - \frac{1}{r_{2}} - \frac{2}{d})$ .....(i)
For a system, $U = \frac{Q^{2}}{2 C_{e q}}$
Equating (i) and (ii), we get
$\frac{1}{C_{e q}} = \frac{1}{4 π \in_{0}} (\frac{1}{r_{1}} + \frac{1}{r_{2}} - \frac{2}{d})$
$C_{e q} = \frac{4 π \in_{0}}{(\frac{1}{r_{1}} + \frac{1}{r_{2}} - \frac{2}{d})}$
If $d \to \infty, C_{e q} = \frac{4 π \in_{0}}{\frac{1}{r_{1}} + \frac{1}{r_{2}}}$
$\frac{1}{C_{e q}} = \frac{1}{4 π \in_{0} r_{1}} + \frac{1}{4 π \in_{0} r_{2}} = \frac{1}{C_{1}} + \frac{1}{C_{2}}$
i.e., the given system is equivalent to two capacitors $C_{1} = 4 π \in_{0} r_{1}$ and $C_{2} = 4 π \in_{0} r_{2}$ in series.
.

.

.

.

Updated on:21/07/2023

Consider two concentric spherical metal shells of radii $r_{1}$ and $r_{2} (r_{2} > r_{1})$ . If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
A $\frac{- r_{2}}{r_{1}} q$
Bzero
C $\frac{- r_{1}}{r_{2}} q$
D $- q$
The radii of two concentric spherical conducting shells are $r_{1} and r_{2} (> r_{1})$ . The change on the oute shell is q. The charge on the inner shell which is connected to the earth is
A $q (\frac{r_{2}}{r_{1}})$
B $q^{2} (\frac{r_{1}}{r_{2}})$
C $- q (r_{1} / r_{2})$
D $q^{2} (\frac{r_{2}}{r_{1}})$
There are two concentric spherical shells with inner shell having positive charge q and outer shell having a charge -q. Now outer shell is supplied a charge -2g and inner shell is earthed, Calculate the ratio of initial and final capacities of the system. (If a = 3R, b= 5 R)

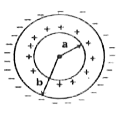A $3 / 5$
B3
C1
D $5 / 3$