Find the gravitational interaction energy of system consisting of a disc of mass M, radius R and a small mass m dituated at a distance x from disc centre on its axis as shown in figure.

Step by step video & image solution for Find the gravitational interaction energy of system consisting of a disc of mass M, radius R and a small mass m dituated at a distance x from disc centre on its axis as shown in figure. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Particle Exercise50videos
GRAVITATION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Discussion Qns31videos
GRAVITATION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - Unsolved Numerical Problems86videos
FLUID MECHANICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.83videos
KINEMATICS
Similar Questions
Find the gravitational potential energy of a system consisting of a uniform rod AB of mass M, length l and a point mass m as shown in figure.
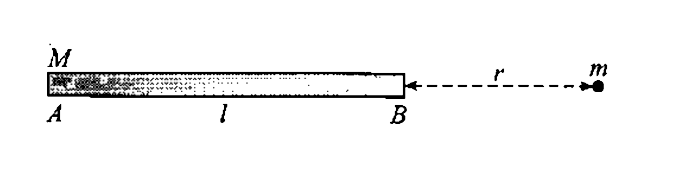 View Solution
View SolutionFind the gravitational potential energy of system consisting of uniform rod AB of mass M, length l and a point mass m as shown in figure.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A small smooth disc of mass m and radius moving with an initial velocity 'v' along the positive x− axis collided with a big disc of mass 2m and radius 2r which was initially at rest with its centre at origin as shown in figure.

If the coefficient of restitution is 0 then velocity of largen disc after collision isA8v27ˆi−2√227vˆjB8v27ˆi+2√227vˆjCv3ˆiD2√227vˆi−8v2ˆj - Question 2 - Select One
A mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass M is
AGMm√2R2BGMm2R2CGMm2√2R2DGMm4R2 - Question 3 - Select One
The moment of inertia of a disc of mass M and radius R about an axis. Which is tangential to sircumference of disc and parallel to its diameter is.
A54MR2B23MR2C32MR2DMR2
The mass of a thin circular plate is M and its radius is R. About an axis in the plane of plate at a perpendicular distance R/2 from centre of plate, its moment of inertia is
View SolutionWhat is the gravitational potential energy of a particle of mass m kept at a distance x from the centre of a disc of mass M on its axis ? The radius of the disc is R.
View SolutionFind the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
View SolutionCalculate gravitational field intensity at a distance x on the axis from centre of a uniform disc of mass M and radius R .
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View Solution

