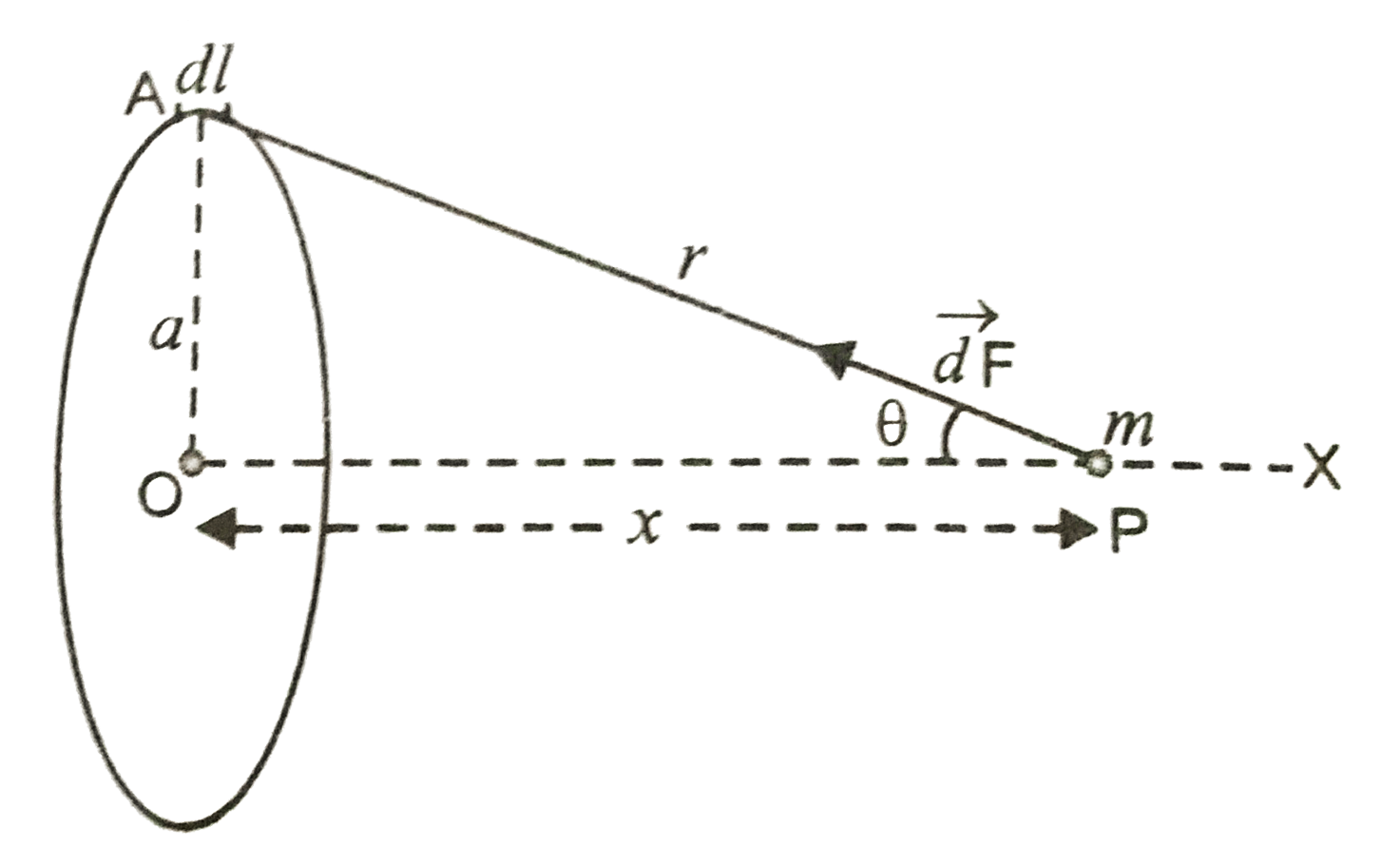
Find the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
Consider a ring of mass M, radius a with centre at O. Mass per unit length of ring =M2πa. Let P be a point on the axis of ring at a distance x from O as shown in Fig. Take an element of length dl of the ring.
Mass of this element of the ring, dM=M2πa×dl.
Gravitational force on the particle of mass m at P due to this element is
dF=GmdMr2=Gm(M/2πa)dlr2
acting along PA where, r=PA=(a2+x2)1/2
Resolving d→F into two rectangular components, we get, dFcosθ acts along the axis directed towards O and dFsinθ acts perpendicular to axis.
now we calculate the force on the particle at P due to all elements of the ring and divide these forces into two rectangular components, along the axis and the perpendicular to the axis of ring. We note that the component of forces perpendicular to the axis due to all elements will cancel each other and component of forces along the axis will add up. So the resultant gravitational force on particle at P due to all element is
F=∫dFcosθ=GmM2πa∫dlr2(xr)
=GmMx2πa(a2+x2)3/2∫dl=GmMx2πa(a2+x2)3/2×2πa=GmMx(a2+x2)3/2
Gravitational intensity at P is, I=Fm=GMx(a2+x2)3/2
In vector from, −−→T=−GMx(a2+x2)3/2ˆx,
where -ve sign shown that the graviational intensity is of attractive field.
Topper's Solved these Questions
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - VALUE BASED QUESTIONS
5 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - CURIOSITY QUESTION
1 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - VERY SHORT ANSWER QUESTIONS
11 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Assertion - Reason Type questions
14 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
Similar Questions
Find the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionA uniform solid of valume mass density ρ and radius R is shown in figure.
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector →l in terms of radius vector →r of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field →E at point P in vector formulationand interpret the result.
View Solution
Knowledge Check
The intensity of gravitational field at a point situated at a distance of 8000km form the centre of the earth is 6/kg. The gravitational potential at that point is -(in joule /kg)
A8×106B2.4×103C4.8×107D6.4×1014
A thin copper ring of radius a is charged with q units of electricity. Calculate the electric field at a point at a distance x from the centre and on the axis of the ring. Use the result to find the electirc field due to a charged disc of surface density of charge ε.
View SolutionCalculate gravitational field intensity at a distance x on the axis from centre of a uniform disc of mass M and radius R .
View SolutionFind potential at a point 'P' at a distance 'x' on the axis away from centre of a uniform ring of mass M and radius R .
View SolutionCalculate the gravitational field intensity and potential at the centre of the base of a solid hemisphere of mass m, radius R
View SolutionWhat is the gravitational potential energy of a particle of mass m kept at a distance x from the centre of a disc of mass M on its axis ? The radius of the disc is R.
View SolutionA charge Q is uniformly on a ring of radius R. Find the electric potential on the axis of ring at distance x from the centre of the ring. Sketch variation of potential with respect to x.
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View Solution
