Find the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.

Consider a ring of radius a, mass M and centre at O.
Mass per unit length =M2πa
P is the point at which gravitational intensity is to be measured.
Let dl is the small element of the ring.
Mass of this element =M2πadl=dM
Let a particle of mass m be placed at point P.
Force on this mass due to small element dl = dF
=GmdMr2
=GmMdl2πar2
∴r=PB=√(a2+x2)
Resolve dF into two perpendicular components, one along the axis of ring and the other perpendicular to the plane of ring. We will find that all components perpendicular to axis due to all elements will cancel each other, whereas the component along the axis of ring will add up.
Therefore, the resultant gravitational force on particle at P due to all elements will be
F=∫dFcosθ
=∫GMm2πa=dlr2cosθ
=∫GMm2πadlr2.xr (cosθ=xr)
=GMm2πaxr3∫dl
=GMm2πa(a2+x2)32.2πa
=GMmx(a2+x2)32
Gravitational intensity at P=I=Fm=GMmxm(a2+x2)32
I=GMx(a2+x2)32
Topper's Solved these Questions
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - NCERT FILE (TEXTBOOK EXERCISES)
23 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - NCERT FILE (Additional Exercises)
4 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Conceptual Questions
19 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
Similar Questions
Find the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionA uniform solid of valume mass density ρ and radius R is shown in figure.
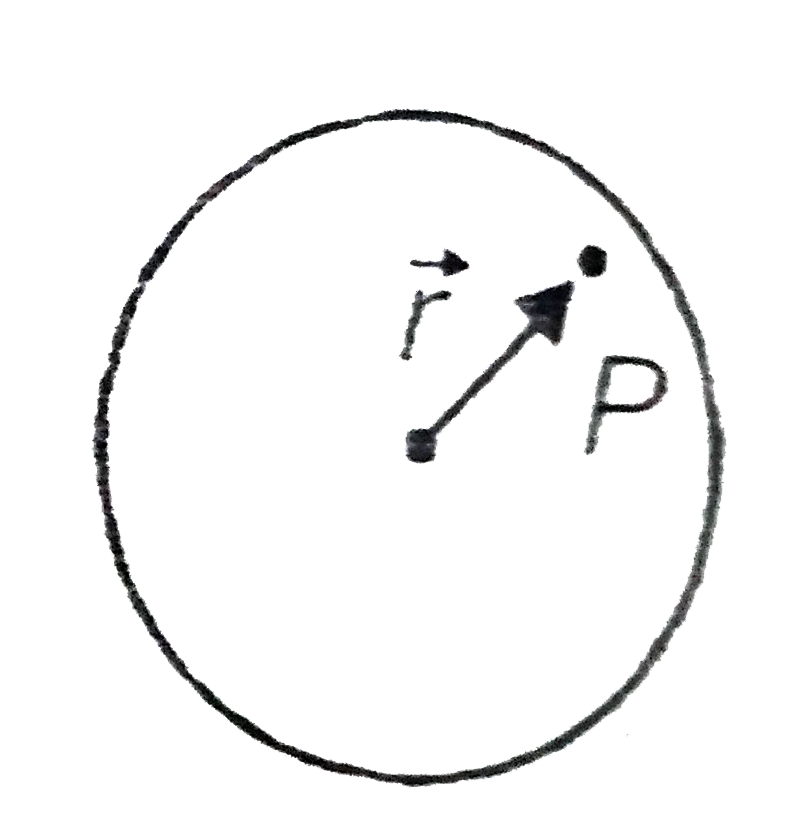
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector →l in terms of radius vector →r of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field →E at point P in vector formulationand interpret the result.
View Solution
Knowledge Check
The intensity of gravitational field at a point situated at a distance of 8000km form the centre of the earth is 6/kg. The gravitational potential at that point is -(in joule /kg)
A8×106B2.4×103C4.8×107D6.4×1014
A thin copper ring of radius a is charged with q units of electricity. Calculate the electric field at a point at a distance x from the centre and on the axis of the ring. Use the result to find the electirc field due to a charged disc of surface density of charge ε.
View SolutionCalculate gravitational field intensity at a distance x on the axis from centre of a uniform disc of mass M and radius R .
View SolutionFind potential at a point 'P' at a distance 'x' on the axis away from centre of a uniform ring of mass M and radius R .
View SolutionCalculate the gravitational field intensity and potential at the centre of the base of a solid hemisphere of mass m, radius R
View SolutionWhat is the gravitational potential energy of a particle of mass m kept at a distance x from the centre of a disc of mass M on its axis ? The radius of the disc is R.
View SolutionA charge Q is uniformly on a ring of radius R. Find the electric potential on the axis of ring at distance x from the centre of the ring. Sketch variation of potential with respect to x.
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View Solution
