Find the magnetic field at the centre O of the loop shown in the figure
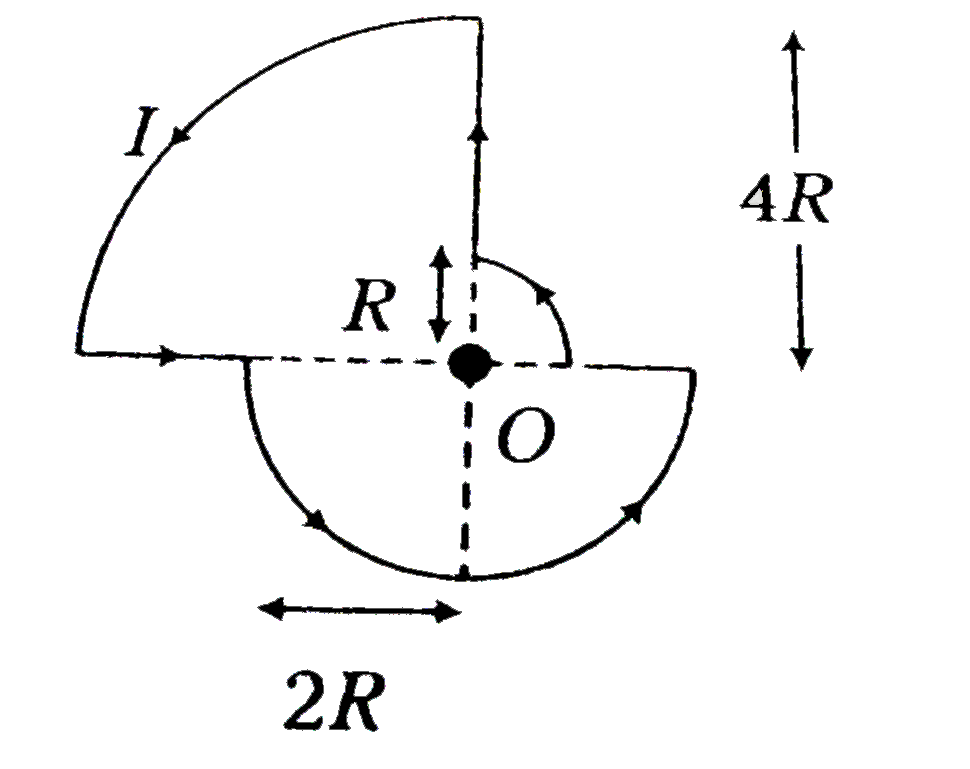
Due to straight parts, there is no magnetic field at O. There are three fields at O
B1=μ0i4π(4R)×π2 (∵B=μ0i4πRθ), due to arc of radius 4R
B2=μ0i4π(2R)(π), due to arc of radius 2R
B3=μ0i4πR(π2), due to arc of radius R
As the current is anticlockwise in all three arcs, therefore, all the fields are prependicular to plane and outwards.
⇒Bnet=B1+B2+B3
∴Bnet=μ0iR[132+18+18]
=9μ0i32R
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Illustration
14 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Try Yourself
27 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
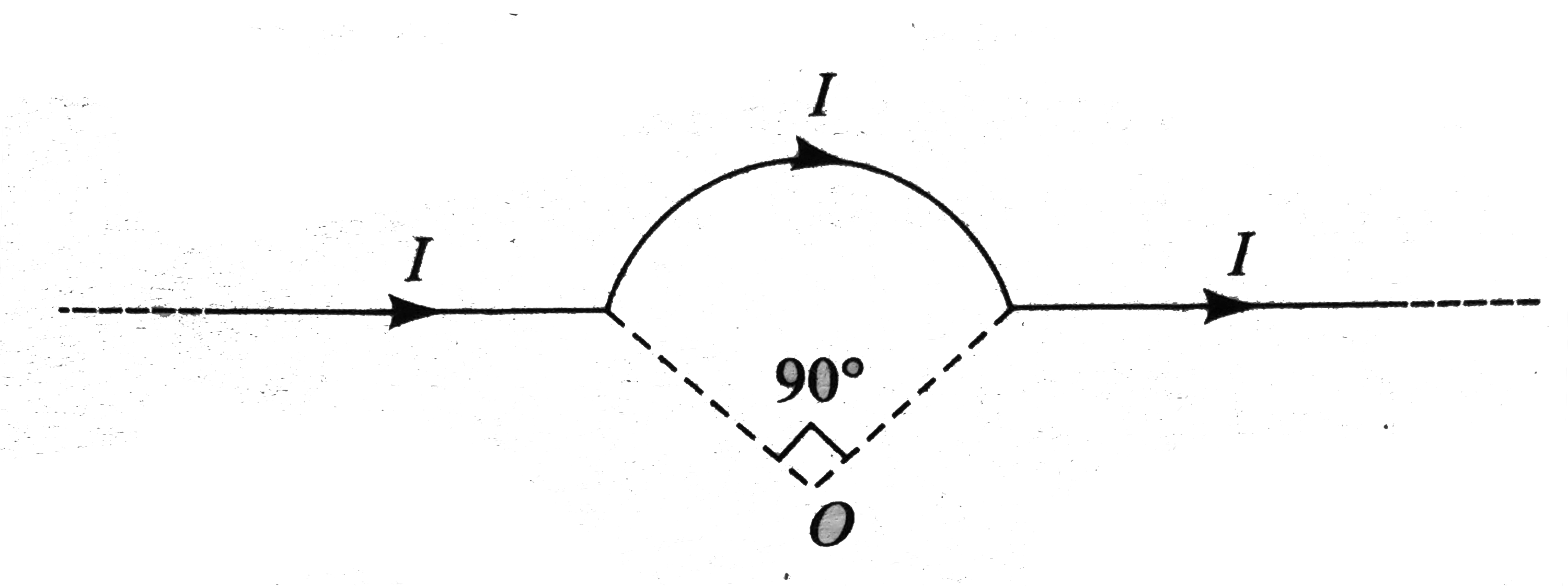
The magnetic field at the centre O of the are shown in the figure is
View SolutionFind the magnetic field at the centre of the circular loop shown in figure.

View SolutionThe wire ABC shown in figure forms an equilateral triangle. Find the magnetic field B at the centre O of the triangle assuming the wire to be uniform.

View SolutionFigure shows a square loop ABCD with edge length a. The resistance of the wire ABC is r and that of ADC is 2r. Find the magnetic field B at the centre of the loop assuming uniform wires.

View SolutionFigure shows a square loop ABCD with edge length a. The resistance of the wire ABC is r and that of ADC is 2r. Find the magnetic field B at the centre of the loop assuming uniform wires.

View SolutionThe magnetic field at centre O of the arc in Fig.

View SolutionAn electric current I flows through a circular loop as shown in Figure 2(b) below. Write an expression and direction for the magnetic field at the centre of the loop at point P.

View SolutionThe magnetic field at the centre of the circular loop as shown in Fig. when a single wire is bent to form a circular loop and also extends to form straight sections is
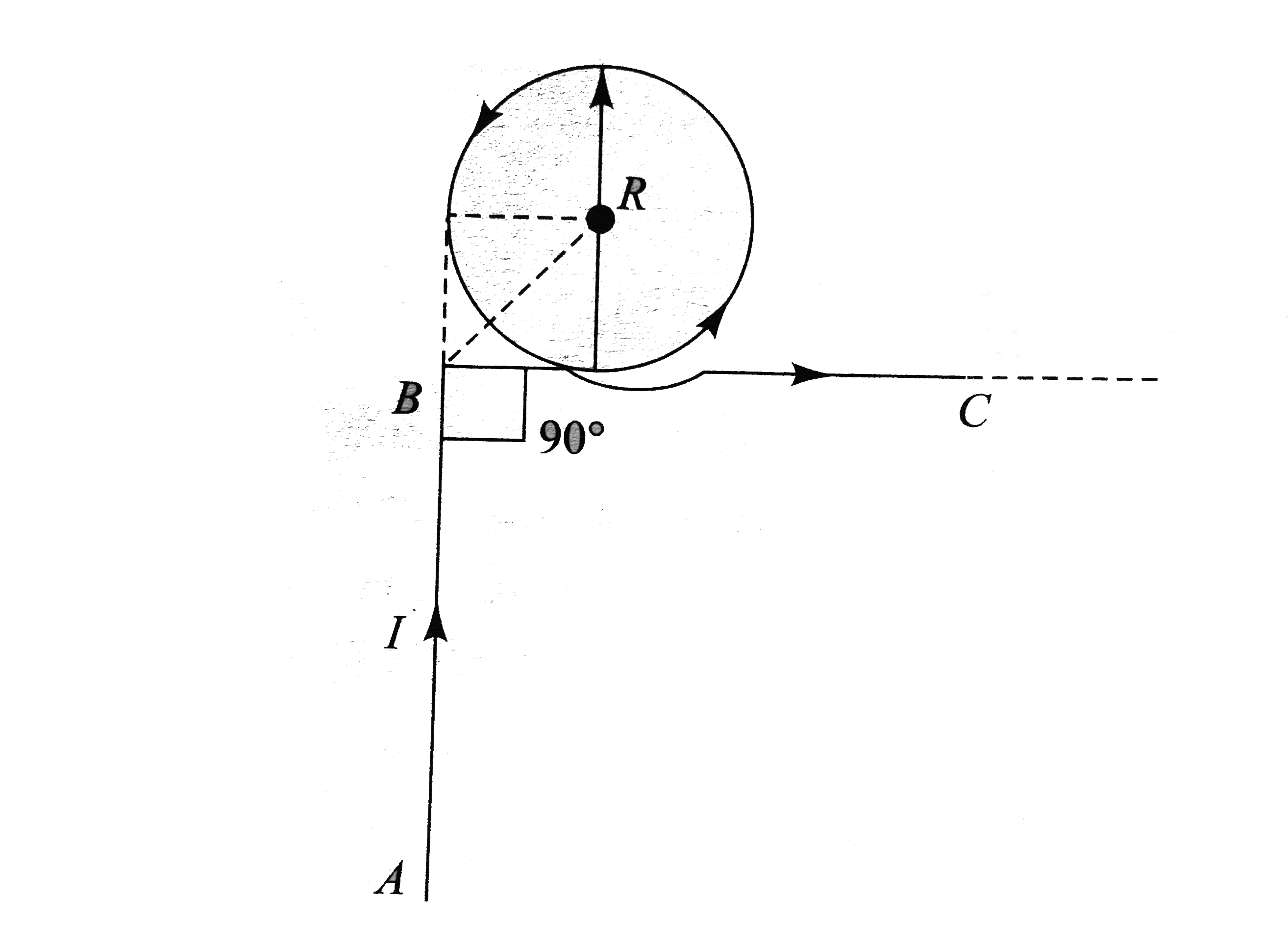
View SolutionA current of2⋅00A exists in a square loop of edge 10⋅0cm. Find the magnetic field B at the centre of the square loop.
View SolutionA wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
View Solution
