Find the magnetic induction due to a straight conductor of length 16cm carrying current of 5A at a distance of 6cm from the midpoint of conductor
To find the magnetic induction (magnetic field) due to a straight conductor of length 16 cm carrying a current of 5 A at a distance of 6 cm from the midpoint of the conductor, we can follow these steps:
1. Identify the Given Data:
- Length of the conductor, L=16cm=0.16m
- Current flowing through the conductor, I=5A
- Distance from the midpoint of the conductor to the point where we want to find the magnetic field, d=6cm=0.06m
2. Determine the Distances:
- Since the conductor is 16 cm long, the distance from the midpoint to each end of the conductor is L2=162=8cm=0.08m.
3. Calculate the Height (h):
- We can visualize a right triangle formed by the distance from the midpoint to the point where we want to find the magnetic field. The height of this triangle is the distance from the midpoint to the point, which is d=0.06m, and the base is 0.08m.
- Using the Pythagorean theorem:
h=√(0.08)2+(0.06)2=√0.0064+0.0036=√0.01=0.1m
4. Calculate Sine Values:
- For angles θ1 and θ2 formed at the point where the magnetic field is being calculated:
sinθ1=0.080.1=0.8
sinθ2=0.080.1=0.8
5. Use the Formula for Magnetic Induction:
- The formula for the magnetic induction B due to a straight current-carrying conductor is given by:
B=μ0I4πd(sinθ1+sinθ2)
- Where μ0=4π×10−7T m/A.
6. Substituting the Values:
- Now substituting the values into the formula:
B=(4π×10−7)×54π×0.06(0.8+0.8)
- The 4π terms cancel out:
B=50.06×1.6×10−7
7. Calculating the Final Value:
- Calculate 50.06=83.33.
- Therefore,
B=83.33×1.6×10−7=1.3333×10−5T
- Rounding off gives:
B≈1.33×10−5T
Final Answer:
The magnetic induction at the point is approximately 1.33×10−5T.
- Length of the conductor, L=16cm=0.16m
- Current flowing through the conductor, I=5A
- Distance from the midpoint of the conductor to the point where we want to find the magnetic field, d=6cm=0.06m
- Since the conductor is 16 cm long, the distance from the midpoint to each end of the conductor is L2=162=8cm=0.08m.
- We can visualize a right triangle formed by the distance from the midpoint to the point where we want to find the magnetic field. The height of this triangle is the distance from the midpoint to the point, which is d=0.06m, and the base is 0.08m.
- Using the Pythagorean theorem:
h=√(0.08)2+(0.06)2=√0.0064+0.0036=√0.01=0.1m
- For angles θ1 and θ2 formed at the point where the magnetic field is being calculated:
sinθ1=0.080.1=0.8
sinθ2=0.080.1=0.8
- The formula for the magnetic induction B due to a straight current-carrying conductor is given by:
B=μ0I4πd(sinθ1+sinθ2)
- Where μ0=4π×10−7T m/A.
- Now substituting the values into the formula:
B=(4π×10−7)×54π×0.06(0.8+0.8)
- The 4π terms cancel out:
B=50.06×1.6×10−7
- Calculate 50.06=83.33.
- Therefore,
B=83.33×1.6×10−7=1.3333×10−5T
- Rounding off gives:
B≈1.33×10−5T
The magnetic induction at the point is approximately 1.33×10−5T.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA
142 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB
71 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
Similar Questions
Knowledge Check
A conductor of length 2 m carrying current 2 A is held parallel to an infinitely long conductor carrying current of 12 A at a distance of 100 mm, the force on small conductor is
A8.6×10−5NB6.6×10−5NC7.6×10−5ND9.6×10−5N
Find the magnetic field at point P due to a straight line segment AB of length 6cm carrying a current of 5A. (See figure)
(μ0=4π×10−7N−A−2).
 .
.
View SolutionMagnetic induction at a point due to a small element of current carrying conductor is
View SolutionA straight conductor of length 32 cm carries a current of 30A. Magnetic induction at a point which is in air at a perpendicular distance of 12cm from the mid point of the conductor is
View SolutionA current l is flowing through a long straight solid conductor of radius R = 4 cm. Magnetic field at a distance 2 cm from the axis of conductor is B0 The distance from the axis, where magnetic field is 1.5 B0 is (current density is uniform)
View SolutionAB and CD are long straight conductor, distance d apart, carrying a current l. The magnetic field at the midpoint of BC is

View SolutionFind magnetic field at O due to the current carrying conductor as shown in the figure.
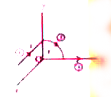
View SolutionA Long straight conductor carrying a current of 2 A is in parallel to another conductor of length 5 cm. and carrying a current 3A. They are separated by a distance of 10 cm. Calculate (a) B due to first conductor at second conductor (b) the force on the short conductor.
View Solution

_PHY_E06_180_Q01.png)