Question

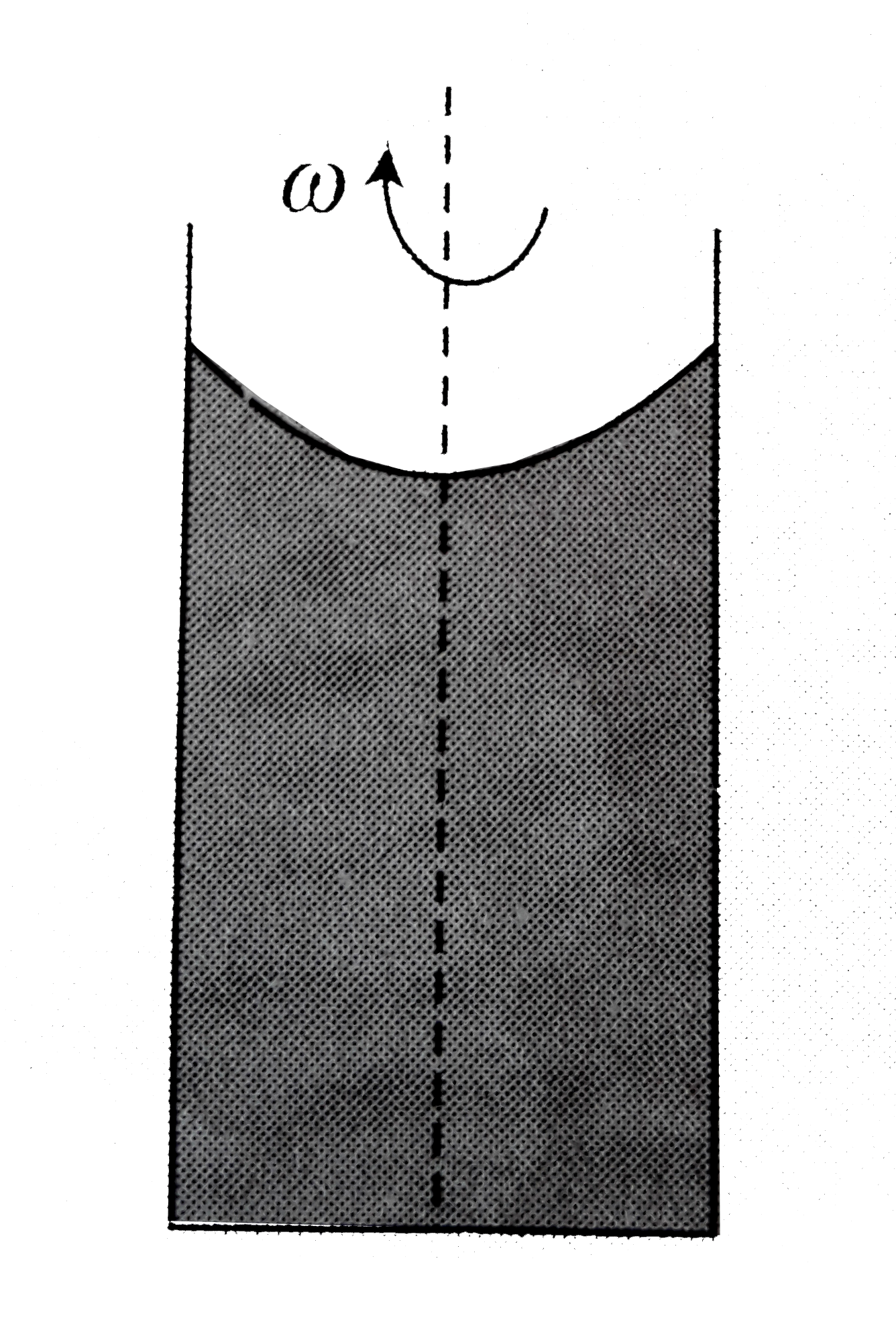
Find the mass of a mole of colloid particles if during their centrifuging with an angular velocity $\omega$ about a vertical axis the concentration of the particles at the distance $r_2$ from the rotation axis is $\eta$ times greater than that at the distance $r_1$ (in the same horizontal plane). The densities of the particles and the solvent are equal to $\rho$ and to ${\rho }_0$ respectively.

Explanation

In a centrifuge rotating with angular velocity `omega` about an axis, there is a centrifugal acceleration `omega^2 r` where `r` is the radial distance from the axis. In a fluid if there are suspened colloidal particle they experience an additional force. If `m` is the mass of each particle then its volume is `(m)/(rho)` and the excess force on this particle is.
`(m)/(rho) (rho - rho_0) omega^2 r` outward corresponding to a potential energy `-(m)/(2 rho)(rho - rho_0) omega^2 r^2`
This gives rise to a concentration variation.
`n(r) = n_0 exp(+ (m)/(2 rho kT)(rho - rho_0) omega^2 r^2)`
Thus `(n(r_2))/(n(r_1)) = eta = exp (+(M)/(2 rho RT) (rho - rho_0) omega^2 (r_2^2 - r_1^2))`
where `(m)/(k) = (M)/(R), M = N_A m` is the molecular weight
Thus `M = (2 rho RT 1n eta)/((rho - rho_0)omega^2(r_2^2 - r_1^2))`.