Find the maximum speed at which a truck can safaly travel without toppling over, on a curve of radius 250m . The height of the centre of gravity of the truck above the ground is 1.5m and the distance between the wheels is 1.5m , the truck being horizontal.
The correct Answer is:C
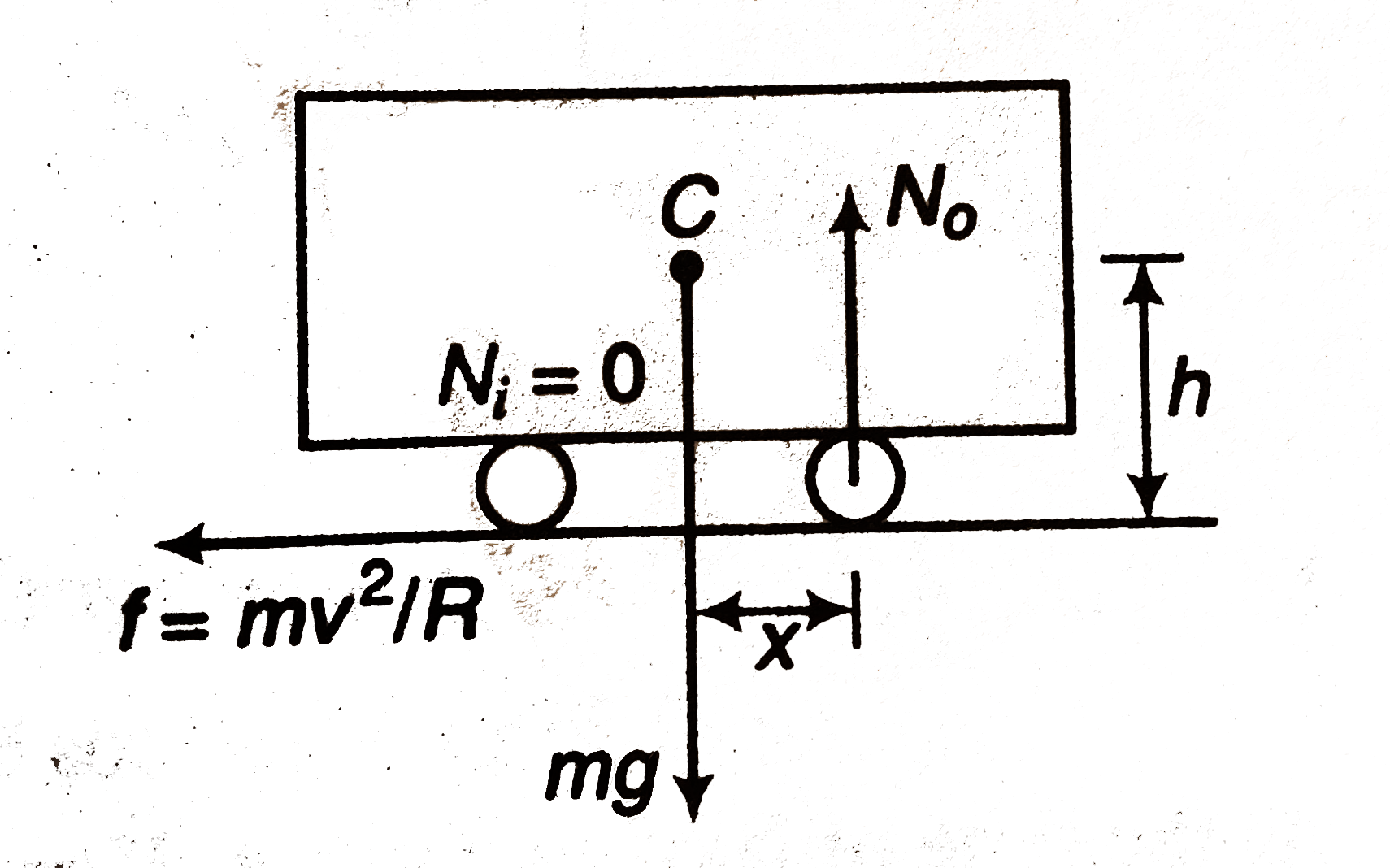
In critical case, normal reaction on inner wheel Ni will become zero. Normal reaction on outer wheel N0=mg . Friction will provide the necessary centripetal force.
:. f=mv2R
Taking moment aboout C
N0(x)=f(h)
or (mg)x=(mv2R)h
:. v=√gRxh
=√9.8×250×0.75L5
=35m/s
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Single Correct18videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 More Than One Correct5videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Objective14videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
A car is speeding on a horizontal road curving round with a radius 60 m The coefficient of friction between the wheels and the road in 0.5 The height of centre of gravity of the car from the road level is 0.3 m and the distance between the wheels is 0 .8 m . Calculate the maximum safe velocity for negotiating the curve . Will the car skid or topple if this velocity is exceeded ?
View SolutionWhat is the greatest speed at which a car having a track width of 1.5m can turn in a circular path of radius 24.5m without overturning ? Assume that the center of gravity of the car is 0.49m above the ground. Take g=9.8m/s2 .
View Solution
Knowledge Check
- Question 1 - Select One
The height of the centre of gravity of the truck above the ground is 1.5 m and the distance between the wheel is 1.5 m .If the maximum velocity at which a truck can safely tavel along the horizontal track withiout toppling on a curve of radius 250 m will be
A30m/sB35m/sC40m/sD45m/s - Question 2 - Select One
The maximum speed (in ms−1 ) with which a car driver can traverse on a horizontal unbanked curve of radius 80 m with coefficient of friction 0.5 without skidding is : (g = 10 m/s2)
A25 m/sB20 m/sC15 m/sDdepends on mass of the car - Question 3 - Select One
The maximum safe speed of a vehicle over a curved road of radius 150 m is 10m/s. If the width of road is 7.5 m, the height of the outer edge will be
A0.25 mB0.50 mC0.30 mD0.60 m
A car of mass m travelling at speed v moves on a horizontal track. The centre of mass of the car describes a circle of radius r. If 2a is the separation of the inner and outer wheels and h is the height of the centre of mass above the ground, show that the limiting speed beyond which the car will overturn in given by
v2=grah
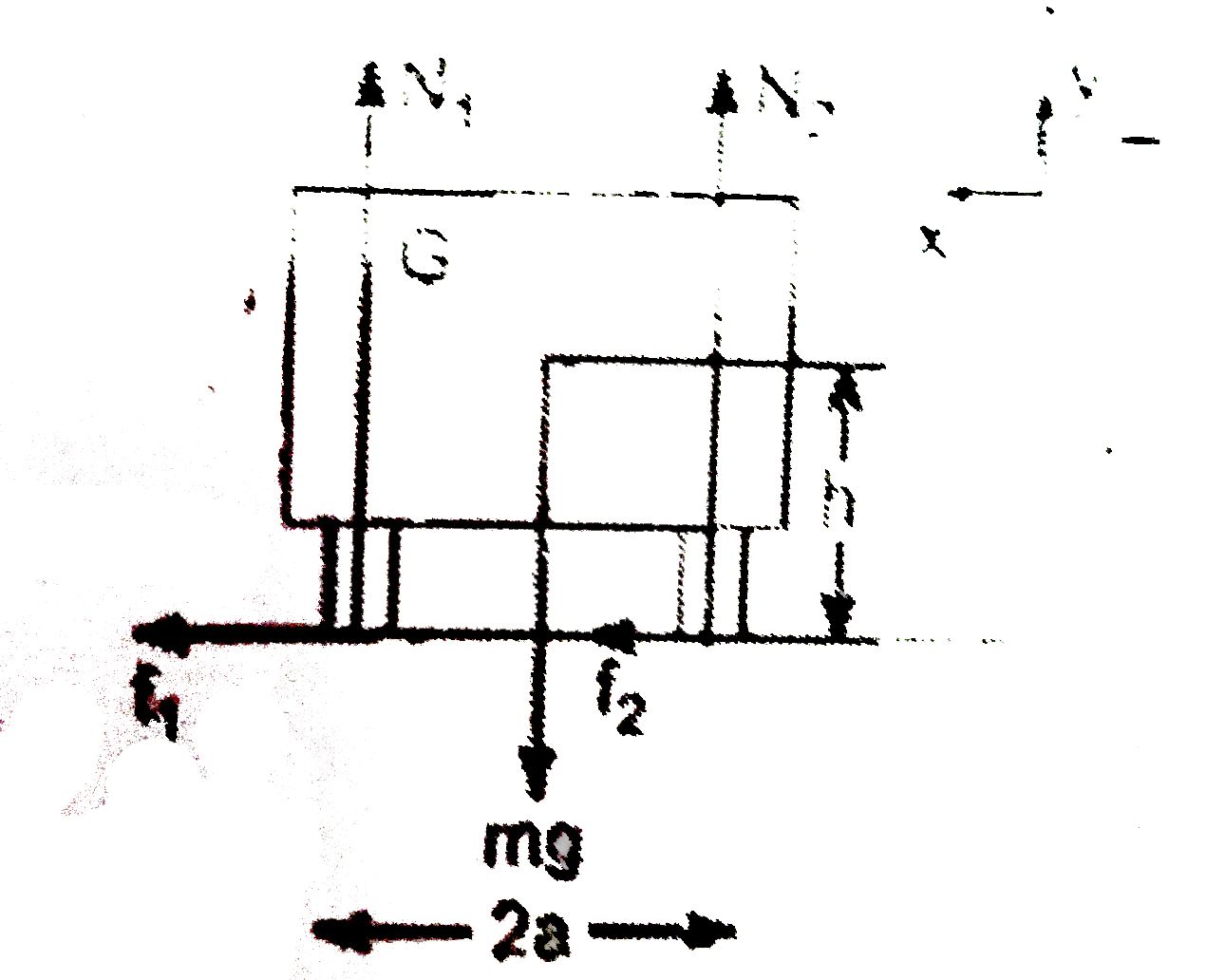 View Solution
View SolutionA crate of egg is located in the middle of the flat bed of a pick up truck as the truck negotiates an unbanked curve in the road. The curve may be regarded as an arc of circle of radius 35m. IF the coefficient of friction between the crate and the flat bed of the truck is 0.6, the speed with which the truck should turn so that the crate does not slide over the bed is
View SolutionThe vertical section of a road over the bridge is in the from of circle of radius 15.5 m What will be the maximum velocity with which a car whose centre of gravity is 0.5 m above the ground can cross the bridge without losing contact with the surface of bridge at the highest point ? (g=9.8m/s2)
View SolutionA car is moving along a horizontal curve of radius 20 m , and coefficient of friction between the road and wheels of the car is 0.25 . If acceleration due to gravity is (9.8m/s2), then its maximum speed is
View SolutionA flyover bridge is in the form of a circular are of radius 39.5 m . What is the limiting speed at which a car can cross the bridge without losing constact with the road , at the highest point ? [Assume that the centre of gravity of the car is 0.5 m above the road and g=10m/s2]
View Solution

